- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ОГЭ Тема: Проценты 9 класс
Содержание
- 1. Подготовка к ОГЭ Тема: Проценты 9 класс
- 2. Цели изучения темы:Повторить и систематизировать знания учащихся по теме «Проценты»Научиться решать задачи приближенные к жизненным ситуациям
- 3. Требования к знаниям и умениям учащихся:Знать:определение процента,
- 4. Понятие процентаПроцент - это одно из
- 5. Слово « процент » происходит
- 6. В простейших задачах на проценты вся величина
- 7. Чтобы найти процент от числа, надо это
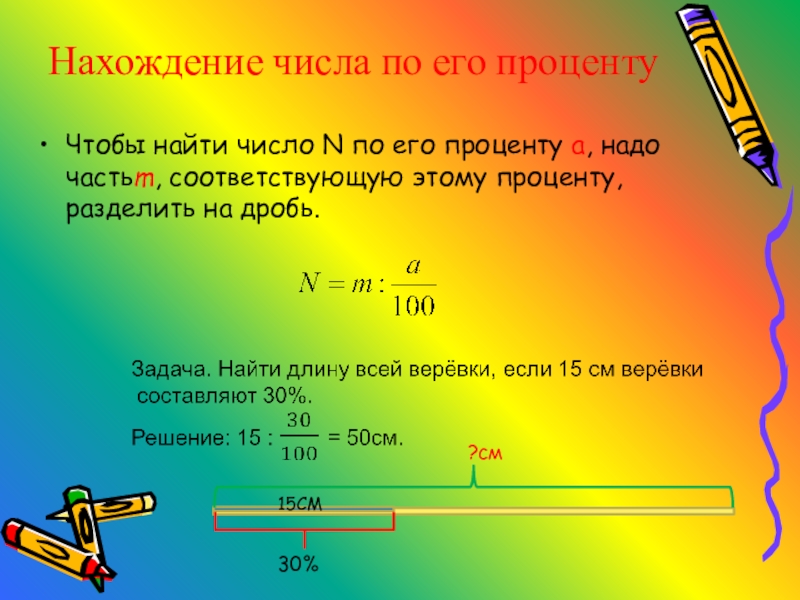
- 8. Чтобы найти число N по его проценту
- 9. Чтобы узнать, сколько процентов одно число составляет
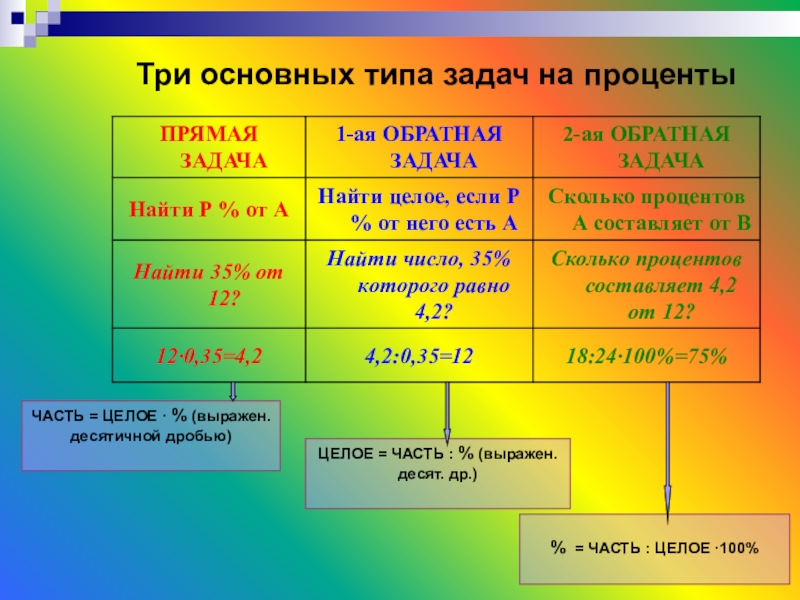
- 10. Три основных типа задач на процентыЧАСТЬ =
- 11. Магазин закупил куклы и стал
- 12. Хр.-закупочная цена , 1,5Хр.-новая цена, 1,56=0,9Х(р.)-предновогодняя цена,Х-0,9Х=0,1х(р.)-разница
- 13. Сбербанк России с 1 августа
- 14. Слайд 14
- 15. Слайд 15
- 16. Формула увеличения числа на заданный процент.
- 17. Слайд 17
- 18. Пример.Сумма с НДС равна 1180 рублей, НДС
- 19. Задачи на проценты в вариантах ОГЭ
- 20. Часть 2Задача 1. Имеются два сплава с
- 21. ЗАДАЧА 1. Сколько граммов воды надо
- 22. Пусть х -количество воды, которое
- 23. Задача 2. В сосуд содержащий 2 кг 80
- 24. Задача на сплавы.Сплав меди и цинка весом
- 25. УДАЧИ НА ЭКЗАМЕНАХ!
Слайд 2Цели изучения темы:
Повторить и систематизировать знания учащихся по теме «Проценты»
Научиться решать
Слайд 3Требования к знаниям и умениям учащихся:
Знать:
определение процента, основные способы решения стандартных
схему работы банка, схему расчета банка с вкладчиками и заемщиками;
основные понятия в задачах на смеси, растворы и сплавы.
Уметь:
решать стандартные задачи на проценты «Нахождение процентов от числа», «Нахождение числа по его процентам», «Изменение величины в процентах»;
решать задачи на начисление простых и сложных процентов;
решать с помощью уравнений задачи на «смеси», «сплавы», «концентрации»
Слайд 4 Понятие процента
Процент - это одно из математических понятий.
Слово процент происходит
что означает «от сотни» или «на 100».
Например: Из 100 выпускников, сдавшие экзамены,
17 получили пятёрки.
17% - Это 17 из 100, 17 человек из 100 человек
Слайд 5 Слово « процент » происходит от латинских слов pro
Историческая справка
Знак % произошел, благодаря опечатке. В рукописях pro centum часто заменяли словом « cento » ( сто) и писали его сокращенно – cto. В 1685 году в Париже была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %
После этой ошибки математики стали употреблять знак % для обозначения процентов.
Слайд 6В простейших задачах на проценты вся величина N принимается за 100%,
Простейшие задачи на проценты
100% - N
a% - m
Слайд 7Чтобы найти процент от числа, надо это число умножить на соответствующую
Нахождение процента от
числа
Например: 15% от 60кг
равны 60·0,15=9 кг
Слайд 8Чтобы найти число N по его проценту a, надо частьm, соответствующую
Нахождение числа по его проценту
?см
30%
15СМ
Слайд 9Чтобы узнать, сколько процентов одно число составляет от второго, надо первое
Нахождение процентного
отношения двух чисел
Задача. Сколько процентов составляет 50г соли в растворе
массой 300г.
Решение:
1) 300 – 50 = 250(г) –вода
2)50:250·100%= 20% соли в растворе.
Слайд 10Три основных типа задач на проценты
ЧАСТЬ = ЦЕЛОЕ · % (выражен.
ЦЕЛОЕ = ЧАСТЬ : % (выражен. десят. др.)
% = ЧАСТЬ : ЦЕЛОЕ ·100%
Слайд 11 Магазин закупил куклы и стал продавать их по цене,
Решение задачи на стоимость.
Слайд 12Хр.-закупочная цена ,
1,5Хр.-новая цена,
1,56=0,9Х(р.)-предновогодняя цена,
Х-0,9Х=0,1х(р.)-разница между ценами,
0,1Х ·
Ответ:10%
Решение:
Слайд 13 Сбербанк России с 1 августа 2009 года начислял доход
Проценты в банке
Слайд 16 Формула увеличения числа на заданный процент.
Сумма с НДС
Пусть
В= A · (1 + P / 100).
Пример 1. Банковский кредит 300 000 рублей под 18%. Общая сумма долга составит.
В= 300000 · (1 + 18/ 100) = 300000 · 1,18 = 354000 рублей.
Пример 2. Сумма без НДС равна 2000 рублей, НДС 16%. Сумма с НДС составляет:
В= 2000 · (1 + 16 / 100) = 2000 · 1,16 = 2320 рубля
Слайд 18Пример.Сумма с НДС равна 1180 рублей, НДС 18 процентов. Стоимость без
В= 1180 / (1 + 0.18) =1000рублей
Слайд 19Задачи на проценты
в вариантах ОГЭ
Часть 1
Задача 1. Некоторый товар
Задача 2. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам от 3 до 10 человек предоставляется скидка в 5%, более 10 человек – 10%. Сколько заплатит за экскурсию группа из 12 человек?
Слайд 20Часть 2
Задача 1. Имеются два сплава с разным содержанием золота. В
Решение. Пусть х – масса первого сплава, у – масса второго сплава. Тогда количество золота в первом сплаве составляет 0,3х, а во втором сплаве 0,55у.
Масса нового сплава равна х+у, а количество золота в нем составляет 0,4 (х+у).
Получим уравнение 0,3х+0,55у = 0,4 (х+у). Преобразуем уравнение, получим:
30х+55у = 40х+40у,
6х+11у = 8х+8у,
3у = 2х. отсюда, х : у = 3 : 2.
Ответ: в отношении 3 : 2.
Задачи на проценты в вариантах ОГЭ
Слайд 21ЗАДАЧА 1. Сколько граммов воды надо добавить к 50г раствора,
Решение задачи на смесь.
Слайд 22
Пусть х -количество воды, которое надо добавить.
Новое количество
50 •0,08 г. Количество соли в новом растворе составляет 5 % от (50 + х)г,
т. е. 0,05(50 + х) г. Т. к. количество соли от добавления воды не изменилось, то оно одинаково в исходном и новом растворах. Получаем уравнение:
50•0,08 = 0,05(50 + Х),
50•8 = 5(50 +Х),
80 = 50 +Х,
Х=30.
Ответ: 30 г.
Решение:
Слайд 23Задача 2. В сосуд содержащий 2 кг 80 % -го водного раствора
Решение:
Масса уксусной кислоты не изменилась, тогда получаем уравнение:
0,01х·5 = 0,8·2
0,05х = 1,6
х = 1,6:0,05
х = 32
Ответ: концентрация получившегося раствора уксусной кислоты равна 32 %.
Слайд 24Задача на сплавы.
Сплав меди и цинка весом 20кг содержит 30% меди.
Решение: