Презентация, доклад на тему Подготовка к ГИА. Реальная математика. Задание № 20

Содержание

В фирме «ЭХ, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле С = 150+11(t-5), где t — длительность

Слайд 1Реальная математика.
Задание №20
Практические расчеты по формулам

Реальная математика.Задание №20Практические расчеты по формулам

Слайд 2В фирме «ЭХ, прокачу!» стоимость поездки на такси (в рублях) длительностью

более 5 минут рассчитывается по формуле С = 150+11(t-5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки. Ответ укажите в рублях.

Решение. Подставим в формулу значение переменной :
 
 
 
Ответ: 183.

 

МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА» №20

В фирме «ЭХ, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле

Слайд 3 Площадь параллелограмма S (в м2) можно вычислить по формуле S=a⋅b⋅sinα, где a,b — стороны параллелограмма (в

метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и sin α =0,5.
Решение. Подставим в формулу известные значения величин: 

 
Ответ: 60.

МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА» №20

Площадь параллелограмма S (в м2) можно вычислить по формуле S=a⋅b⋅sinα, где a,b — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь

Слайд 4
Площадь параллелограмма S(в м2) можно вычислить по формуле S=ah где а-

сторона параллелограмма h- высота проведенная к этой стороне(в метрах). Пользуясь этой формулой найдите высоту h, если площадь параллелограмма равна 18 м2 , а сторона 3,6 м.
Решение.Выразим высоту  из формулы площади параллелограмма:
 
 
Подставляя, получаем:


 Ответ: 5.

Площадь параллелограмма S(в м2) можно вычислить по формуле S=ah где а- сторона параллелограмма h- высота проведенная к

Слайд 5В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец

рассчитывается по формуле C=6500+4000n, где n — число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец. Ответ укажите в рублях.

Ре­ше­ние. Подставим количество колец в формулу для расчета стоимости. Имеем:
 
 
Ответ: 50 500.

МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА» №20

В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6500+4000n, где n

Слайд 6Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние ss по

формуле s=nl, где n — число шагов, l— длина шага. Какое расстояние прошёл человек, если l=80 , n=1600? Ответ выразите в километрах.
Ре­ше­ние. Найдём какое рас­сто­я­ние прошёл че­ло­век, под­ста­вим длину шага и число шагов в фор­му­лу:
 
 
Ответ: 1,28

МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА» №20

Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние ss по формуле s=nl, где n — число шагов, l— длина шага. Какое

Слайд 7Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t,

где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 10 с. Ответ дайте в километрах, округлив его до целых.
Решение. Найдем расстояние, на котором находится наблюдатель от места удара молнии:

 
Ответ: 3.

МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА» №20

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой

Слайд 8Из формулы центростремительного ускорения a = ω2R  найдите R  (в метрах), если ω =

4 с−1 и a = 64 м/с2.

Решение. Выразим из данной формулы R и подставим значения ω и a:
 
 
Ответ: 4.

МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА» №20

Из формулы центростремительного ускорения a = ω2R  найдите R  (в метрах), если ω = 4 с−1 и a = 64 м/с2.Решение.

Слайд 9
РАЗНЫЕ ЗАДАЧИ

РАЗНЫЕ ЗАДАЧИ

Слайд 10
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле

T=2√l , где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

Решение. Подставим в формулу значение :  

 
Ответ: 2,25.

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле T=2√l , где l — длина нити (в

Слайд 11
Радиус описанной около треугольника окружности можно найти по формуле  

, где   а— сторона треугольника,    —
противолежащий этой стороне угол, а    — радиус описанной около этого треугольника окружности. Пользуясь этой формулой, найдите  , если  , а  .
Решение. Выразим из формулы   :

Подставляя, получаем:


Ответ: 0,4.





Радиус описанной около треугольника окружности можно найти по формуле  

Слайд 12
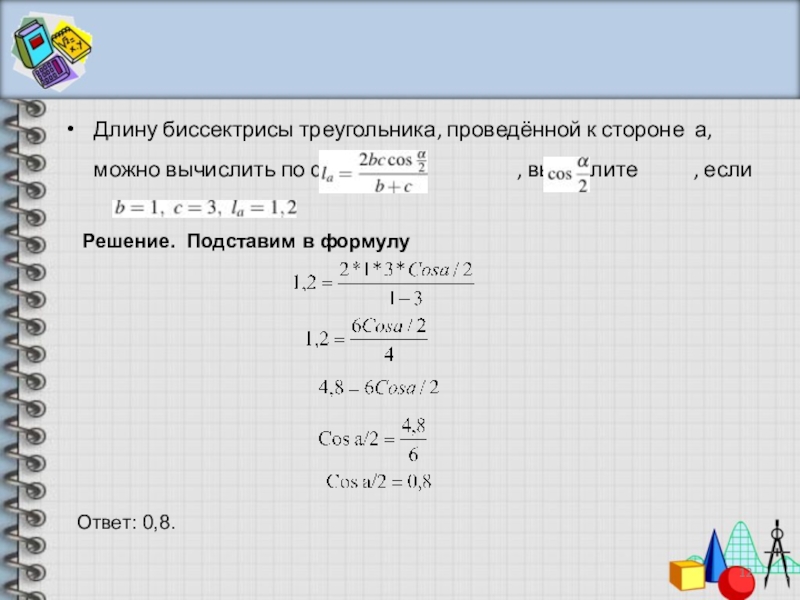
Длину биссектрисы треугольника, проведённой к стороне  а, можно вычислить по формуле 

, вычислите  , если

Ре­ше­ние. Подставим в формулу


Ответ: 0,8.

Длину биссектрисы треугольника, проведённой к стороне  а, можно вычислить по формуле 

Слайд 13
За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет

за t минут, если будет ехать с той же скоростью? Запишите соответствующее выражение.

Решение. Скорость велосипедиста равна 7 : 20 = 0,35 км/мин. Следовательно, за t минут он проедет 0,35t километров.
 
Ответ: 0,35t.

За 20 минут велосипедист проехал 7 километров. Сколько километров он проедет за t минут, если будет ехать с той

Слайд 14
За 25 минут велосипедист проехал 8 километров. За сколько минут он

проедет a километров, если будет ехать с той же скоростью? Запишите соответствующее выражение.

Решение задачи: Составим пропорцию:
25 минут - 8 км
x минут - а км





Ответ: 25a/8


За 25 минут велосипедист проехал 8 километров. За сколько минут он проедет a километров, если будет ехать

Слайд 15
ЛИНЕЙНЫЕ УРАВНЕНИЯ

ЛИНЕЙНЫЕ УРАВНЕНИЯ

Слайд 16
Длину окружности l можно вычислить по формуле l=2πR, где R — радиус окружности (в метрах). Пользуясь этой

формулой, найдите радиус окружности, если её длина равна 78 м. (Считать  π =3).
Ре­ше­ние. Вы­ра­зим ра­ди­ус из фор­му­лы длины окруж­но­сти:

Под­став­ляя, по­лу­ча­ем:

Ответ: 13.

Длину окружности l можно вычислить по формуле l=2πR, где R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её

Слайд 17
Площадь ромба    можно вычислить

по формуле 
где     — диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ  , если диагональ равна 30 м, а пло­щадь ромба 120 м2.
Решение. Подставим в формулу известные величины:
 


Ответ: 8.
Площадь ромба    можно вычислить по формуле 

Слайд 18
Площадь треугольника    можно вычислить по

формуле
где   а — сторона треугольника,  h — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону а  , если площадь треугольника равна 28 м2  , а высота h   равна 14 м.
Решение. Выразим сторону  из формулы площади треугольника:

Подставляя, получаем:

Ответ: 4.

Площадь треугольника    можно вычислить по формуле где   а — сторона

Слайд 19
Площадь треугольника можно вычислить по формуле
где  b

и с  и   — стороны треугольника, а    — угол между этими сторонами. Пользуясь этой формулой, найдите площадь треугольника, если    = 30°,   c= 5,  b = 6.
Решение.Подставим известные значения величин в формулу для нахождения площади:
 



Ответ: 7,5.

Площадь треугольника можно вычислить по формуле где  b и с  и   — стороны треугольника,

Слайд 20
Площадь треугольника можно вычислить по формуле  
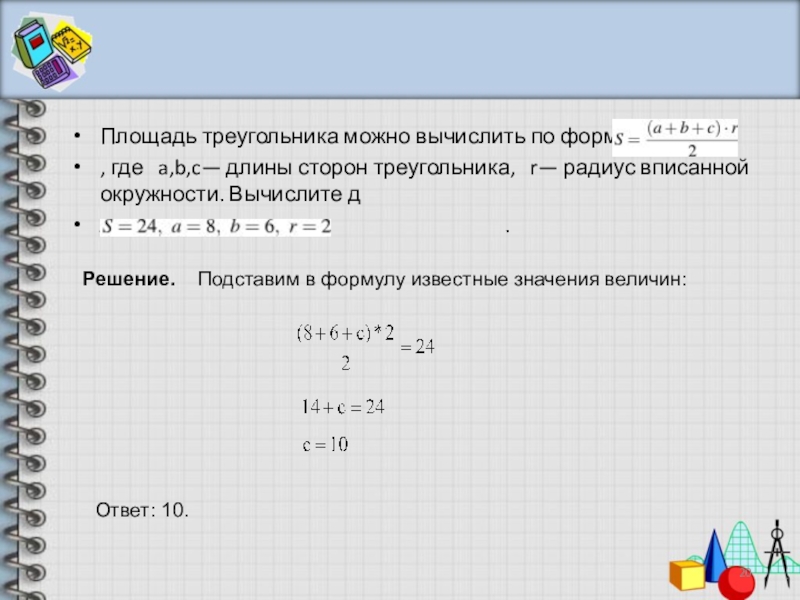
, где   a,b,c— длины сторон

треугольника,   r— радиус вписанной окружности. Вычислите д
лину стороны c  , если   .

Решение. Подставим в формулу известные значения величин:

Ответ: 10.

Площадь треугольника можно вычислить по формуле  , где   a,b,c— длины сторон треугольника,   r— радиус вписанной окружности. Вычислите

Слайд 21
Площадь трапеции    можно вычислить

по формуле
 где  a,b — основания трапеции,  h — высота (в метрах). Пользуясь этой формулой, найдите высоту h , если основания трапеции равны  5 м и 7 м  и  , а её площадь 24 м2  .

Подставим в формулу значения:

Ответ: 4.

Площадь трапеции    можно вычислить по формуле  где  a,b — основания трапеции,

Слайд 22
Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле

 , где   a и b    — катеты, а   c — гипотенуза треугольника. Пользуясь этой формулой, найдите b , если   
и a=6 .
Решение. Подставим в формулу известные значения величин:

Ответ: 3,2.

Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле

Слайд 23
Объём пирамиды вычисляют по формуле  

,
где   S— площадь основания пирамиды,  h — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Решение. Выразим высоту пирамиды из формулы для ее объема:
 

Подставляя, получаем:

Ответ: 8.

Объём пирамиды вычисляют по формуле   , где   S— площадь

Слайд 24
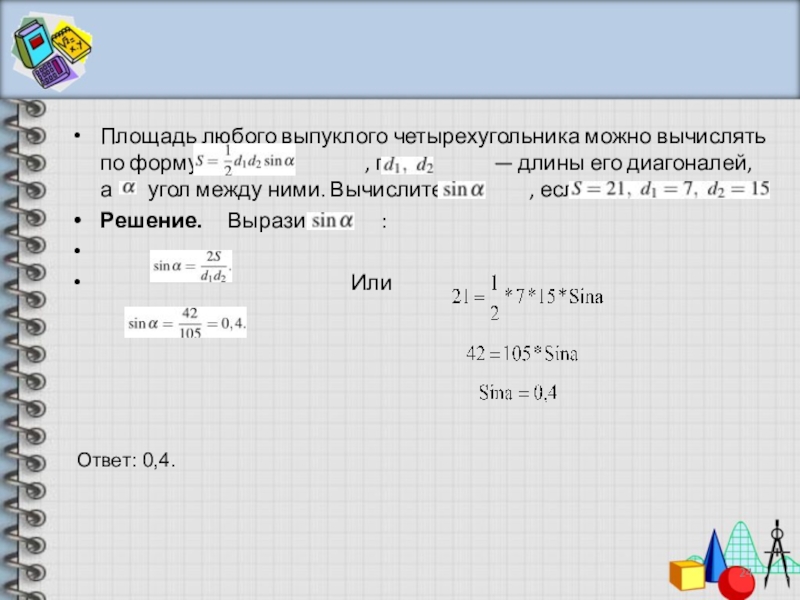
Площадь любого выпуклого четырехугольника можно вычислять по формуле  

, где    — длины его диагоналей, а    угол между ними. Вычислите  , если  
Решение. Выразим :

Или

Ответ: 0,4.

Площадь любого выпуклого четырехугольника можно вычислять по формуле  

Слайд 25
Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта

(t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.
Решение. Подставим в формулу значение переменной F :

Ответ: −14,4.

Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы

Слайд 26
Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта

(t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура (в градусах) по шкале Фаренгейта соответствует 20° по шкале Цельсия?

Решение. Подставим значение температуры в формулу :

Ответ: 68.

Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы

Слайд 27
Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по

формуле   где   — угловая скорость (в с−1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с−1, а центростремительное ускорение равно 45 м/c2.

Решение. Выразим радиус окружности:  Подставим значения переменных   a и 

Или подставим числовые значения величин:

Ответ: 5.

Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле 

Слайд 28
Из закона всемирного тяготения 

 выразите массу  m  и найдите её величину (в килограммах), если  F=13,4 H, r=5 м,
  и гравитационная постоянная 

Решение. Выразим массу
  Подставим значения переменных:

Ответ: 1000.

Из закона всемирного тяготения   выразите массу  m

Слайд 29
Полную механическую энергию тела (в джоулях) можно вычислить по формуле  

где m — масса тела (в килограммах),   v— его
скорость (в м/с),   h— высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите h  (в метрах), если     а v=5 м/с, m=4 кг, а
Решение: Подставим числовые значения величин

Ответ: 5.

Полную механическую энергию тела (в джоулях) можно вычислить по формуле  

Слайд 30
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в

амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 150 ватт, а сила тока равна 5 амперам.

Решение: Подставим числовые значения величин
150=52 *R
150=25R
R=6

Ответ: 6.

Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой,

Слайд 31
Автомобиль проехал 200 километров и израсходовал при этом a литров бензина. Сколько литров

бензина потребуется, чтобы проехать 37 километров при таких же условиях езды? Запишите соответствующее выражение.


Решение. Расход бензина составляет a : 200 = 0,005a л/км. Значит, чтобы проехать 37 километров при тех же условиях езды, потребуется 0,005a · 37 = 0,185a л бензина.

Ответ: 0,185а.

Автомобиль проехал 200 километров и израсходовал при этом a литров бензина. Сколько литров бензина потребуется, чтобы проехать 37 километров

Слайд 32
Закон Кулона можно записать в виде 

 где  F — сила взаимодействия зарядов (в ньютонах),   и   — величины зарядов (в кулонах),   — коэффициент пропорциональности (в Н·м2/Кл2 ), а   r— расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда   (в кулонах), если    Н·м2/Кл2, 
 Кл,   м, а   Н.
Решение. Выразим заряд   из закона Кулона:






Ответ: 0,004.

Закон Кулона можно записать в виде   где 

Слайд 33
Закон всемирного тяготения можно записать в виде
  где  F —

сила притяжения между телами (в ньютонах),   и    — массы тел (в килограммах),  r— расстояние между центрами масс (в метрах), а   — гравитационная постоянная, равная 6.67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела   (в килограммах), если   Н,  кг, а r=2 м.

Решение. Выразим массу    из закона всемирного тяготения:

Подставляя, получаем:

Ответ: 4000.

Закон всемирного тяготения можно записать в виде   где  F — сила притяжения между телами (в ньютонах), 

Слайд 34
Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I —

сила тока (в амперах), R — сопротивление цепи (в омах), а t — время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 2187Дж,  I = 9 A, R = 3 Ом.

Решение: Подставим числовые значения величин

Ответ: 9

Закон Джоуля–Ленца можно записать в виде Q = I2Rt, где Q — количество теплоты (в джоулях), I — сила тока (в амперах), R — сопротивление цепи

Слайд 35
Площадь четырёхугольника можно вычислить по формуле  
где     — длины

диагоналей четырёхугольника,   α— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали   если     a  S=4.

Решение. Выразим длину диагонали  из формулы для площади четырёхугольника:
 

Подставляя, получаем:

Ответ: 4.

Площадь четырёхугольника можно вычислить по формуле  где     — длины диагоналей четырёхугольника,   α— угол между диагоналями.

Слайд 36
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём

(в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.
Решение. Выразим температуру из закона Клапейрона-Менделеева:
  PV = νRT,

Подставляя, получаем:

Ответ: 400.

Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T —

Слайд 37
Задачи для самостоятельного решения

Задачи для самостоятельного решения

Слайд 38
В фирме «ЭХ, прокачу!» стоимость поездки на такси (в рублях) длительностью

более 5 минут рассчитывается по формуле С = 150+11(t-5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 15-минутной поездки. Ответ укажите в рублях.
Ответ: 260.

В фирме «ЭХ, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле С = 150+11(t-5), где t — длительность поездки, выраженная в минутах. Пользуясь этой формулой, рассчитайте стоимость 10-минутной поездки. Ответ укажите в рублях.
Ответ: 205.

В фирме «ЭХ, прокачу!» стоимость поездки на такси (в рублях) длительностью более 5 минут рассчитывается по формуле

Слайд 39
Зная длину своего шага, человек может при­ближённо подсчитать пройденное им расстояние

s по формуле s = nl, где n— число шагов, l — длина шага. Какое расстояние прошёл че­ловек, если l = 70 см, n = 1400? Ответ выразите в километрах.
Ответ:0,98.

Зная длину своего шага, человек может при­ближённо подсчитать пройденное им расстояние s по формуле s = nl, где n— число шагов, l — длина шага. Какое расстояние прошёл че­ловек, если l = 50 см, n = 1200? Ответ выразите в километрах.
Ответ:0,6.

Зная длину своего шага, человек может при­ближённо подсчитать пройденное им расстояние s по формуле s = nl,

Слайд 40
Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t,

где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 17 с. Ответ дайте в километрах, округлив его до целых.
Ответ: 6.

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 17 с. Ответ дайте в километрах, округлив его до целых.
Ответ: 5.

Расстояние s (в метрах) до места удара молнии можно приближённо вычислить по формуле s = 330t, где t — количество секунд, прошедших между вспышкой

Слайд 41
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле

T=2√l , где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 7 секунд
Ответ: 12,25.
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле T=2√l , где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 14 секунд.
Ответ: 49.

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле T=2√l , где l — длина нити (в

Слайд 42
За 25 минут пешеход прошёл 2 километра. Сколько километров он пройдёт

за t  минут, если будет идти с той же скоростью? Запишите соответствующее выражение.

Ответ: 0,08t

За 40 минут пешеход прошёл 3 километра. За сколько минут он пройдёт  a  километров, если будет идти с той же скоростью? Запишите соответствующее выражение.

Ответ: 40а/3
За 25 минут пешеход прошёл 2 километра. Сколько километров он пройдёт за t  минут, если будет идти с той

Слайд 43
Центростремительное ускорение (в м/c2) вычисляется по формуле  α = ω2R, где ω — угловая скорость

(в с–1), R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5 с–1, а центростремительное ускорение равно 35 м/c2 .

Ответ: 1,4.
Центростремительное ускорение (в м/c2) вычисляется по формуле  α = ω2R, где ω — угловая скорость (в с–1), R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 4 с–1, а центростремительное ускорение равно 64 м/c2 .

Ответ: 4.

Центростремительное ускорение (в м/c2) вычисляется по формуле  α = ω2R, где ω — угловая скорость (в с–1), R — радиус окружности. Пользуясь этой

Слайд 44
Закон Кулона можно записать в виде 

 где  F — сила взаимодействия зарядов (в ньютонах),   и   — величины зарядов (в кулонах),   — коэффициент пропорциональности (в Н·м2/Кл2 ), а   r— расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда   (в кулонах), если    Н·м2/Кл2, 
 Кл,   м, а   Н.

Ответ: 0,009.

Закон Кулона можно записать в виде   где 

Слайд 45
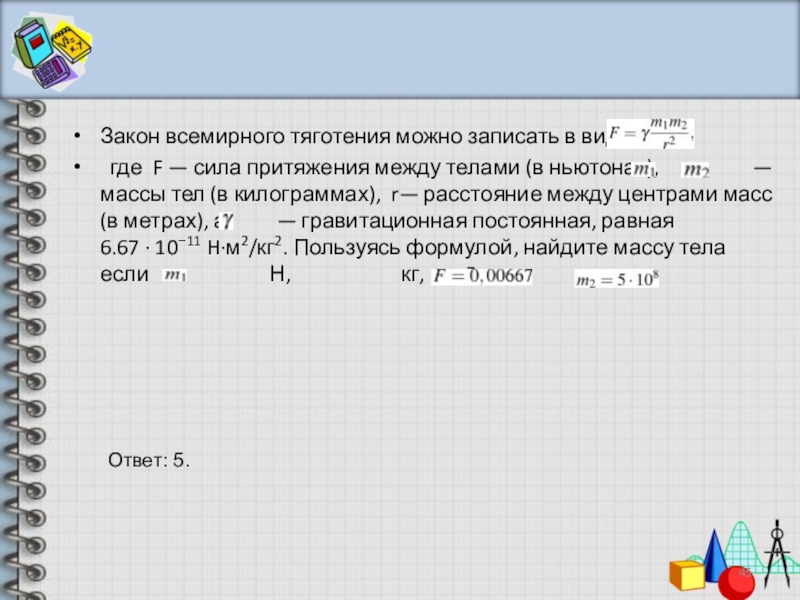
Закон всемирного тяготения можно записать в виде
  где  F —

сила притяжения между телами (в ньютонах),   и    — массы тел (в килограммах),  r— расстояние между центрами масс (в метрах), а   — гравитационная постоянная, равная 6.67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела   (в килограммах), если   Н,  кг, а r=5 м.

Ответ: 5.

Закон всемирного тяготения можно записать в виде   где  F — сила притяжения между телами (в ньютонах), 

Слайд 46
Площадь четырёхугольника можно вычислить по формуле  
где     — длины

диагоналей четырёхугольника,   α— угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали
если а

Ответ: 15.

Площадь четырёхугольника можно вычислить по формуле  где     — длины диагоналей четырёхугольника,   α— угол между диагоналями.

Слайд 47
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём

(в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 700 К, P = 20 941,2 Па, V = 9,5 м3.

Ответ: 34,2.

Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T —
Скачать презентацию

Похожие презентации

Презентация по алгебре Решение показательных уравнений Презентация по алгебре Решение показательных уравнений 204
Презентация внеурочного занятия по математике для учащихся 7-9 классов Презентация внеурочного занятия по математике для учащихся 7-9 классов 250
Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем. Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем. 447
Презентация по теме: Решение задач на концентрацию, сплавы, движение (9-11 классы) Презентация по теме: Решение задач на концентрацию, сплавы, движение (9-11 классы) 265
Презентация по математике для 8-9 класса Решение неполных квадратных уравнений Презентация по математике для 8-9 класса Решение неполных квадратных уравнений 273
Презентация по математике Линейная функция, её свойства и график 7 класс Презентация по математике Линейная функция, её свойства и график 7 класс 217

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть