- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ГИА 9 класс( алгебра).Решение задач на проценты,концентрацию,растворы,сплавы.
Содержание
- 1. Подготовка к ГИА 9 класс( алгебра).Решение задач на проценты,концентрацию,растворы,сплавы.
- 2. Цель урока Организовать работу по отработке и
- 3. Задачи на проценты ПовторениеОпределение 1%50% числа Х
- 4. ЗадачиЦену на товар повысили на 100%, а
- 5. Задачи3. Цена повысилась на 25%. После первого
- 6. Решить самостоятельно4. Сбербанк в конце года начисляет
- 7. Задачи на концентрацию, смеси и сплавыВ задачах
- 8. Задачи1. Смешали 8 кг 12%-го раствора и
- 9. Задачи2. К 120г. раствора, содержащего 80% соли
- 10. Решить самостоятельноСколько литров 3% раствора надо добавить
- 11. Решить самостоятельноПри смешивании первого раствора кислоты, концентрация
- 12. Задача на сплавыИмеются 2 сплава с разным
- 13. Образовательные ресурсыЛысенко Ф.Ф. Предпрофильная подготовка. Итоговая аттестация
Цель урока Организовать работу по отработке и применению теоретических знаний по теме «Решение задач на проценты, растворы, сплавы»Способствовать развитию умений и навыков в решении задач по заданной теме
Слайд 1Алгебра.
Решение задач. 9 класс
Подготовка к ОГЭ(ГИА)
Учитель математики МАОУ СОШ №56
г.Калининград
Зубрихина В.В
Слайд 2Цель урока
Организовать работу по отработке и применению теоретических знаний по
теме «Решение задач на проценты, растворы, сплавы»
Способствовать развитию умений и навыков в решении задач по заданной теме
Способствовать развитию умений и навыков в решении задач по заданной теме
Слайд 3Задачи на проценты
Повторение
Определение 1%
50% числа Х – это его половина
25%
числа Х – это его ¼ ч. (0,25х)
20% числа – (0.2х)
75% числа – (0,75х или 3/4 х)
100% числа – это все число х;
Нахождение процентов от числа (Найти 18% от числа 40. 40*0.18 = 7.2)
Нахождение числа по его процентам (Найти число, 15% которого равны 30. 30 /0.15 = 3000 /15=200)
Нахождения процентного отношения чисел (Сколько процентов составляет 150 от 600? 150/600 *100% = 25%)
Увеличить (уменьшить) на 100% т.е – в 2 раза;
Увеличить (уменьшить) на 50% - в 1.5 раза;
Увеличить (уменьшить) на 25% - в 4 раза;
20% числа – (0.2х)
75% числа – (0,75х или 3/4 х)
100% числа – это все число х;
Нахождение процентов от числа (Найти 18% от числа 40. 40*0.18 = 7.2)
Нахождение числа по его процентам (Найти число, 15% которого равны 30. 30 /0.15 = 3000 /15=200)
Нахождения процентного отношения чисел (Сколько процентов составляет 150 от 600? 150/600 *100% = 25%)
Увеличить (уменьшить) на 100% т.е – в 2 раза;
Увеличить (уменьшить) на 50% - в 1.5 раза;
Увеличить (уменьшить) на 25% - в 4 раза;
Слайд 4Задачи
Цену на товар повысили на 100%, а затем снизили на 50%.
Как изменится цена товара?
Решение:
Первоначальная цена – а
После повышения – 2а (т.к в 2 раза, на 100%)
После понижения – а (на 50%, т.е на половину)
Ответ: не изменится
2. Поездка по железной дороге на новом экспресс, позволила сократить время с 10 часов до 6 часов. На сколько процентов уменьшилось время поездки?
Решение:
10-6=4(ч) – на столько уменьшилось;
4/10 * 100% = 40% (Столько процентов 4 ч. от 10 часов)
Ответ: на 40%
Решение:
Первоначальная цена – а
После повышения – 2а (т.к в 2 раза, на 100%)
После понижения – а (на 50%, т.е на половину)
Ответ: не изменится
2. Поездка по железной дороге на новом экспресс, позволила сократить время с 10 часов до 6 часов. На сколько процентов уменьшилось время поездки?
Решение:
10-6=4(ч) – на столько уменьшилось;
4/10 * 100% = 40% (Столько процентов 4 ч. от 10 часов)
Ответ: на 40%
Слайд 5Задачи
3. Цена повысилась на 25%. После первого повышения цена товара повысилась
на 30%, а потом еще на 5%. После второго повышения, цены товаров сравнялись. Найдите, на сколько процентов первоначальная цена одного товара больше первоначальной цены другого товара.
Решение:
Пусть х руб. – стоимость одного товара; у руб. – стоимость второго товара;
х+0.3х=1.3х (руб.) цена товара после повышения
1.3х+1.3*0.05х=1.365х (руб.) – стал стоить один товар после второго повышения.
у+0.25у=1.25у (руб.) стоимость второго товара после повышения
Т.к цены товаров сравнялись, то получаем уравнение
1,365х=1.25у
у=1.365х / 1.25
у=1.092х
Найдем у/х = 1.092, затем найдем % содержание , т.е 1.092*100%=109,2% - составляет у, а х составляет 100%; то 109,2% – 100% = 9.2%.
Ответ: 9.2%
Решение:
Пусть х руб. – стоимость одного товара; у руб. – стоимость второго товара;
х+0.3х=1.3х (руб.) цена товара после повышения
1.3х+1.3*0.05х=1.365х (руб.) – стал стоить один товар после второго повышения.
у+0.25у=1.25у (руб.) стоимость второго товара после повышения
Т.к цены товаров сравнялись, то получаем уравнение
1,365х=1.25у
у=1.365х / 1.25
у=1.092х
Найдем у/х = 1.092, затем найдем % содержание , т.е 1.092*100%=109,2% - составляет у, а х составляет 100%; то 109,2% – 100% = 9.2%.
Ответ: 9.2%
Слайд 6Решить самостоятельно
4. Сбербанк в конце года начисляет 4% годовых к сумме,
находящийся на счету в начале года. Каким станет первоначальный вклад в 2500 рублей через 1 год, через 2 года?
Слайд 7Задачи на концентрацию, смеси и сплавы
В задачах этого типа обычно присутствуют
3 величины, соотношение между которыми, позволяет составить уравнение
концентрация (доля чистого вещества в смеси)
количество чистого вещества в смеси (или в сплаве)
масса смеси (сплава)
Можно записать соотношение между этими величинами:
масса смеси*концентрацию = количество чистого вещества
Условие и решение задачи удобно помещать в таблицы.
концентрация (доля чистого вещества в смеси)
количество чистого вещества в смеси (или в сплаве)
масса смеси (сплава)
Можно записать соотношение между этими величинами:
масса смеси*концентрацию = количество чистого вещества
Условие и решение задачи удобно помещать в таблицы.
Слайд 8Задачи
1. Смешали 8 кг 12%-го раствора и 12кг 8%-го раствора серной
кислоты. Определите процентное содержание серной кислоты получившегося раствора. Ответ округлите до целых.
Решение:
1.92 : 20 * 100% = 9.6%
Ответ: 10%
Решение:
1.92 : 20 * 100% = 9.6%
Ответ: 10%
Слайд 9Задачи
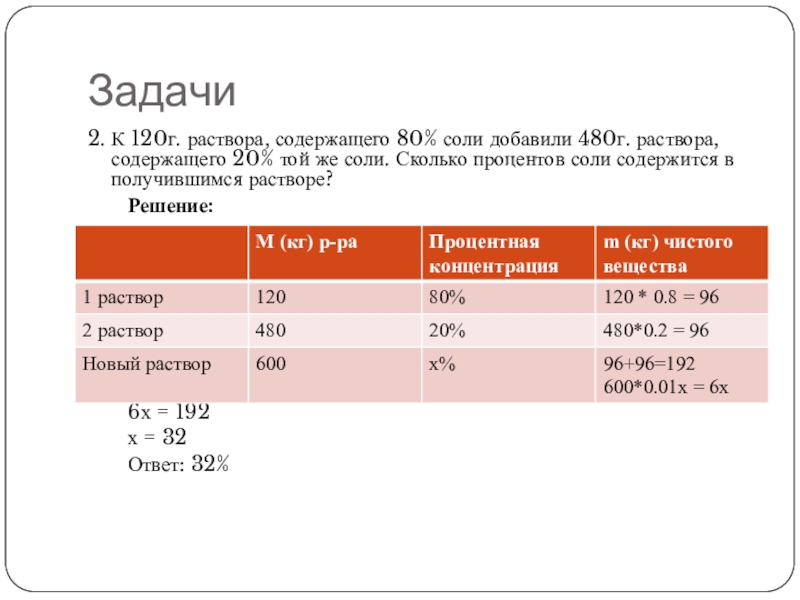
2. К 120г. раствора, содержащего 80% соли добавили 480г. раствора, содержащего
20% той же соли. Сколько процентов соли содержится в получившимся растворе?
Решение:
6х = 192
х = 32
Ответ: 32%
Решение:
6х = 192
х = 32
Ответ: 32%
Слайд 10Решить самостоятельно
Сколько литров 3% раствора надо добавить к 1 литру 6%
раствора, чтобы получить 5% раствор?
Уравнение: 0,03х+0,06 = (х+1)*0,05
х=0.5
Ответ: 0.5 л.
Уравнение: 0,03х+0,06 = (х+1)*0,05
х=0.5
Ответ: 0.5 л.
Слайд 11Решить самостоятельно
При смешивании первого раствора кислоты, концентрация которого 20%, и второго
раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
Слайд 12Задача на сплавы
Имеются 2 сплава с разным содержанием золота. В первом
сплаве содержится 35% золота, во втором 60%. В каком отношении надо взять первый и второй сплав, чтобы получить новый сплав содержащий 40% золота.
Уравнение: 0.35х + 0.6у = (х+у)*0.4
35х+60у = 40х+40у
20у = 5х
4у = х
х/у = 4/1
Ответ: 4:1
Уравнение: 0.35х + 0.6у = (х+у)*0.4
35х+60у = 40х+40у
20у = 5х
4у = х
х/у = 4/1
Ответ: 4:1
Слайд 13Образовательные ресурсы
Лысенко Ф.Ф. Предпрофильная подготовка. Итоговая аттестация – 2012. – М.,
2012
Кузнецова Л.В и др. Сборник заданий для проведения письменного экзамена по математике за курс основной школы – М., 2013
Кузнецова Л.В и др. Сборник заданий для подготовки к итоговой аттестации в 9 классе – М.: «Просвещение», - 2013
Кузнецова Л.В и др. Сборник заданий для проведения письменного экзамена по математике за курс основной школы – М., 2013
Кузнецова Л.В и др. Сборник заданий для подготовки к итоговой аттестации в 9 классе – М.: «Просвещение», - 2013