- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Первообразная
Содержание
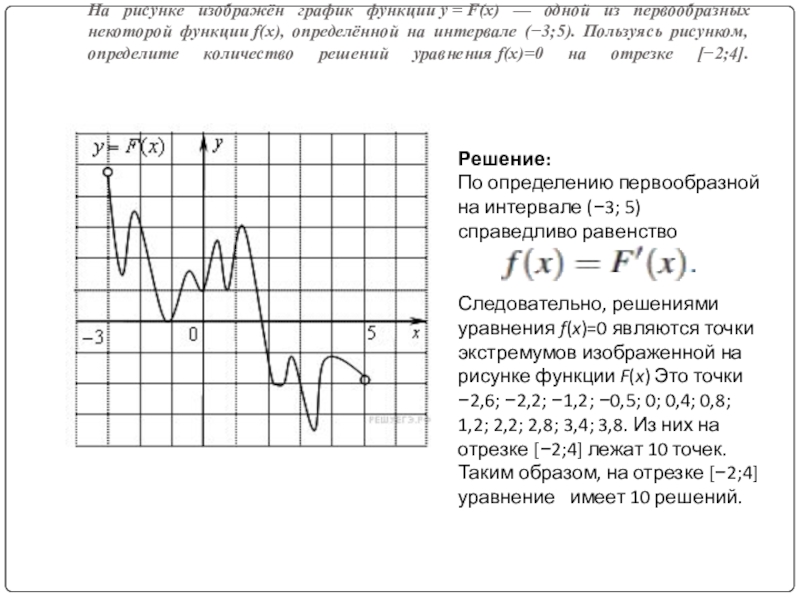
Слайд 2На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f(x),
Решение:
По определению первообразной на интервале (−3; 5) справедливо равенство
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x) Это точки −2,6; −2,2; −1,2; −0,5; 0; 0,4; 0,8; 1,2; 2,2; 2,8; 3,4; 3,8. Из них на отрезке [−2;4] лежат 10 точек. Таким образом, на отрезке [−2;4] уравнение имеет 10 решений.
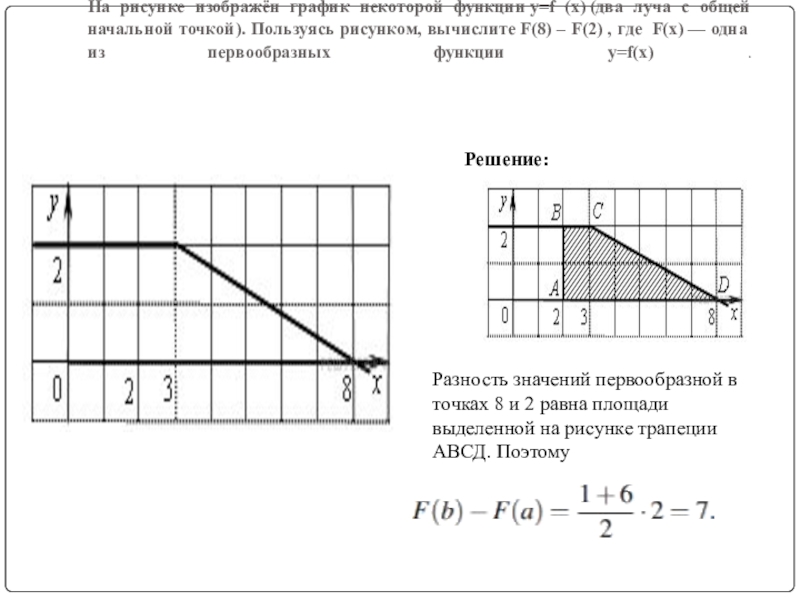
Слайд 3На рисунке изображён график некоторой функции y=f (x) (два луча с общей начальной
Решение:
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции АВСД. Поэтому
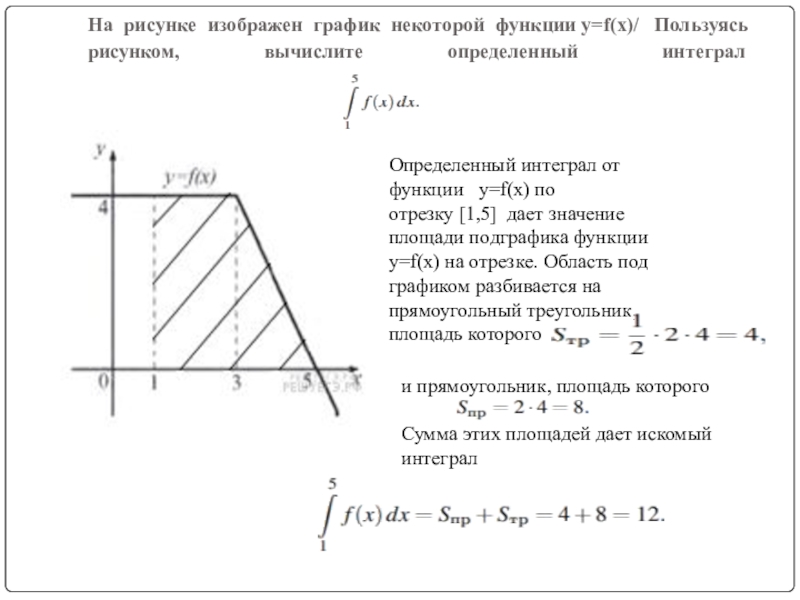
Слайд 4На рисунке изображен график некоторой функции y=f(x)/ Пользуясь рисунком, вычислите определенный интеграл
Определенный интеграл от функции y=f(x) по отрезку [1,5] дает значение площади подграфика функции y=f(x) на отрезке. Область под графиком разбивается на прямоугольный треугольник, площадь которого
и прямоугольник, площадь которого
Сумма этих площадей дает искомый интеграл
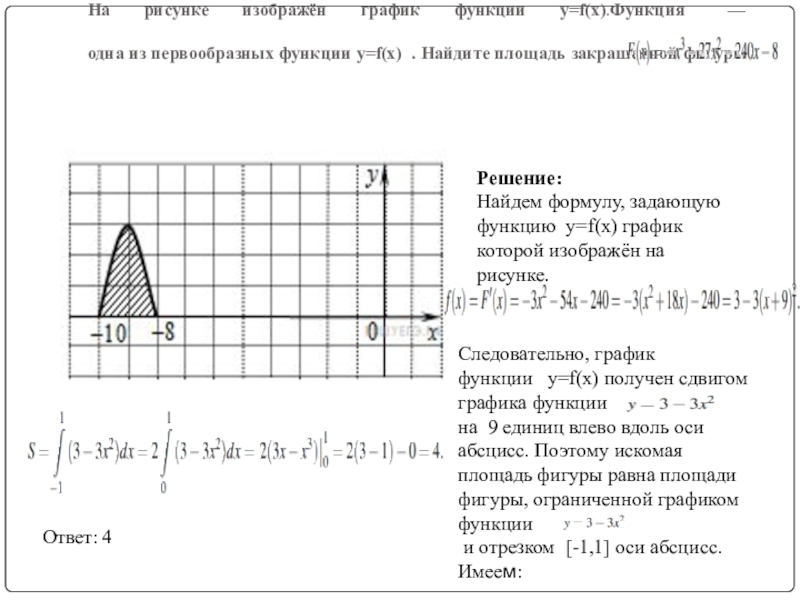
Слайд 5На рисунке изображён график функции y=f(x).Функция — одна из первообразных функции
Решение:
Найдем формулу, задающую функцию y=f(x) график которой изображён на рисунке.
Следовательно, график функции y=f(x) получен сдвигом графика функции
на 9 единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции
и отрезком [-1,1] оси абсцисс. Имеем:
Ответ: 4