- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок по алгебре. Примеры комбинаторных задач
Содержание
- 1. Открытый урок по алгебре. Примеры комбинаторных задач
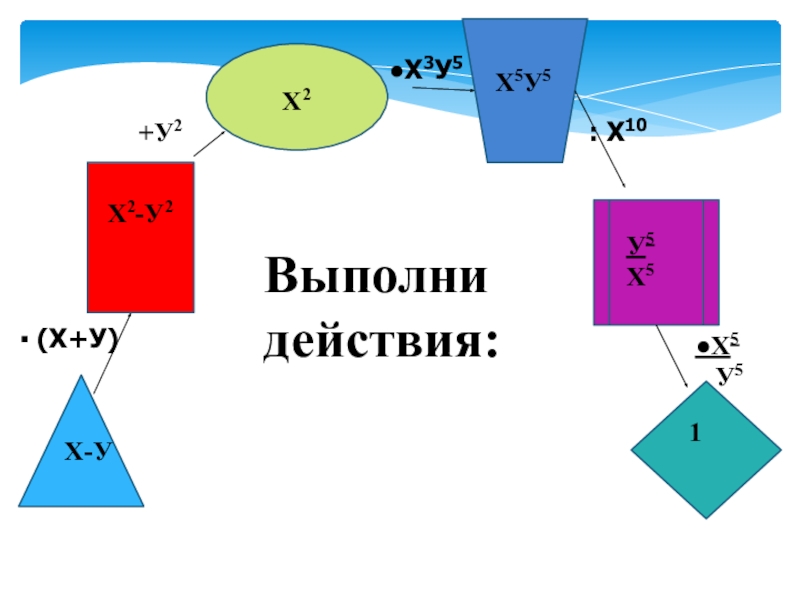
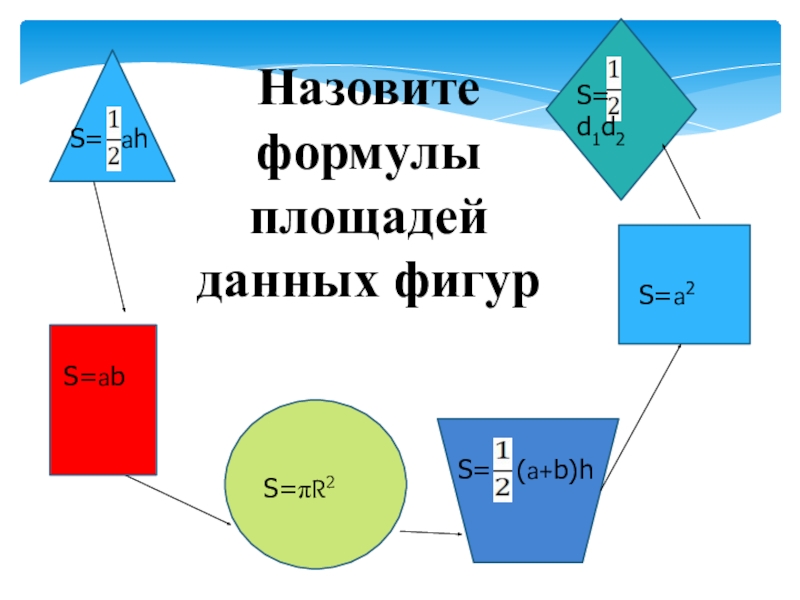
- 2. S=abS=πR2S= (a+b)h S= ahНазовите формулы площадей данных фигурS= d1d2S=a2
- 3. Определите соответствие.1. (a + b)22. (a -
- 4. Однажды крестьянину понадобилось перевезти через реку волка,
- 5. Решение:
- 6. § ЭЛЕМЕНТЫ КОМБИНАТОРИКИ Глава V ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7. Примеры комбинаторных задачТема урока:15.03.20199 класс1 урок
- 8. сформировать представление о комбинаторных задачах, формировать умение
- 9. Сформировать и закрепить у учащихся навыки решения
- 10. Термин «комбинаторика» был введён в математический обиход
- 11. Познакомимся с некоторыми приемами решения комбинаторных
- 12. №715У Ирины 5 подруг: Вера, Зоя, Марина,
- 13. Составим сначала все пары, в которые входит
- 14. Рассмотрим еще одну задачу. На цветочной клумбе
- 15. РешениеВсего 3+2+1=6Ответ:6 вариантовшшшжжбббжммм
- 16. Слайд 16
- 17. Приемы решения комбинаторных задач дерево возможных
- 18. Заметим, что ответ на вопрос,
- 19. Правило умножения, иначе называемое правилом «и» —
- 20. Решите задачу, используя дерево возможных
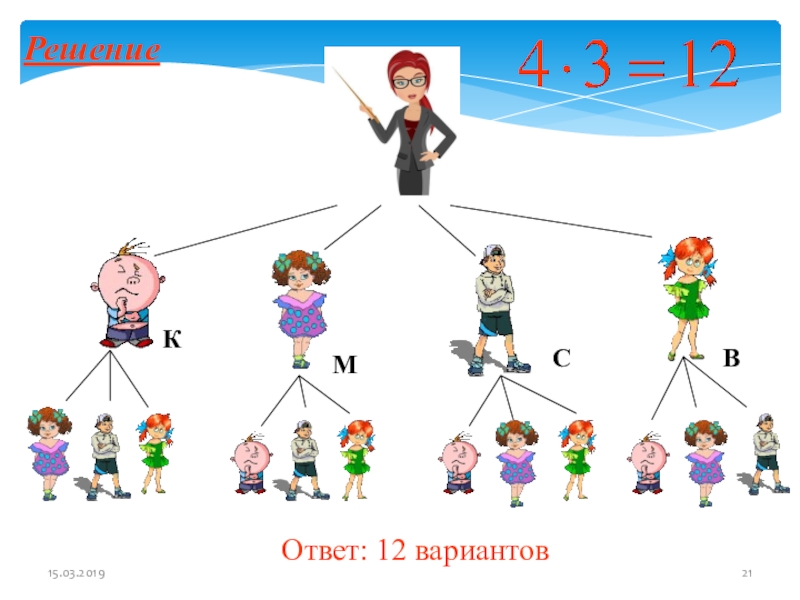
- 21. Ответ: 12 вариантов РешениеКСМВ
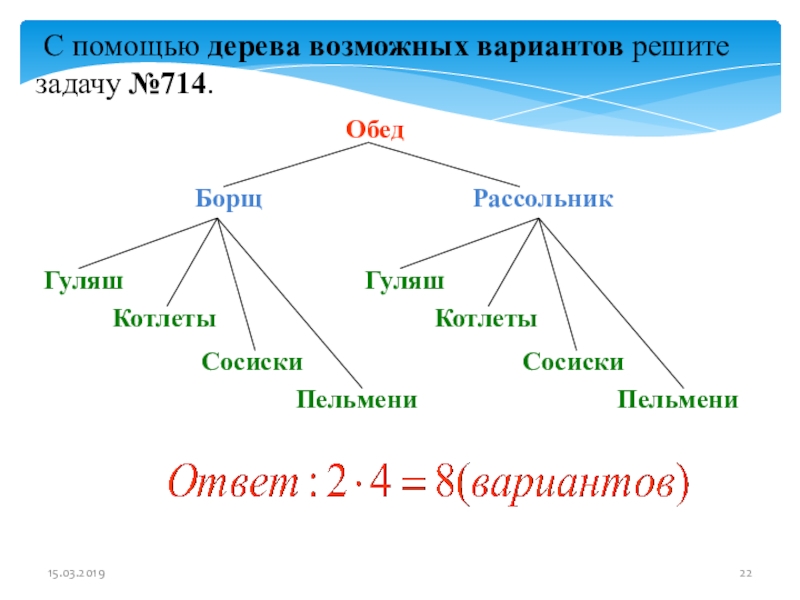
- 22. С помощью дерева возможных вариантов решите
- 23. Слайд 23
- 24. Задачи на закреплениеС помощью дерева возможных вариантов решите задачу №714.№ 717,720№728 – правило умножения
- 25. Примеры каких задач были рассмотрены сегодня на
- 26. Домашнее задание:п. 30 (комбинаторное правило умножения)№ 716
- 27. Существует много видов комбинаторных задач, это лишь некоторые из них.Спасибо за внимание!
Слайд 3Определите соответствие.
1. (a + b)2
2. (a - b)2
3. 32 - b2
4.
5. 9 - 6х + х2
6. 16a2 – 8a + 1
7. (4 – z)(4 +z)
1. 16 – z2
2. a2 – 2ab + b2
3. (m - n)2
4. (4a - 1)2
5. (3 – b)(3 + b)
6. (3 – х)2
7. a2 + 2ab + b2
Слайд 4Однажды крестьянину понадобилось перевезти через реку волка, козу и капусту. У крестьянина
задача
Слайд 8сформировать представление о комбинаторных задачах,
формировать умение решать комбинаторные задачи различными
продолжить работу по созданию условий, обеспечивающих успешное участие обучающихся в ГИА-2019
цели урока:
Слайд 9Сформировать и закрепить у учащихся навыки решения комбинаторных задач.
Воспитать умение выделять
Продолжать развивать самоконтроль и взаимоконтроль, опыт общения при работе в парах.
Совершенствовать навыки решения комбинаторных задач; продолжать подготовку к экзамену в новой форме в процессе планового урока.
Задачи урока
Слайд 10Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем,
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Слайд 11Познакомимся с некоторыми
приемами решения комбинаторных задач
решение методом перебора;
решение
решение с помощью комбинаторного правила умножения;
Слайд 12№715
У Ирины 5 подруг: Вера, Зоя, Марина, Полина и Светлана. Она
Замечание. При решении для краткости будем писать первые буквы имен.
Слайд 13Составим сначала все пары, в которые входит Вера.
ВЗ, ВМ, ВП,
Выпишем теперь пары, в которые входит Зоя, но не входит Вера.
Далее составим пары, в которые входит Марина, но не входят Вера и Зоя.
Еще одна пара
ЗМ, ЗП, ЗС
МП, МС
ПС
Всего существует 4+3+2+1=10
Решение
Ответ:10 вариантов
Вера
Зоя
Марина
Полина
Света
Получим 4 пары.
Таких пар три.
Их две.
Далее составим пары, в которые входит Полина.
Слайд 14Рассмотрим еще одну задачу. На цветочной клумбе сидели шмель, жук, бабочка
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
ш
ж
б
м
Слайд 16 Таким образом, из
Ответ: 9 чисел.
Приемы решения комбинаторных задач
метод перебора
11;14;17; (начали с 1)
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
41;44;47; (начали с 4)
71;74;77; (начали с 7)
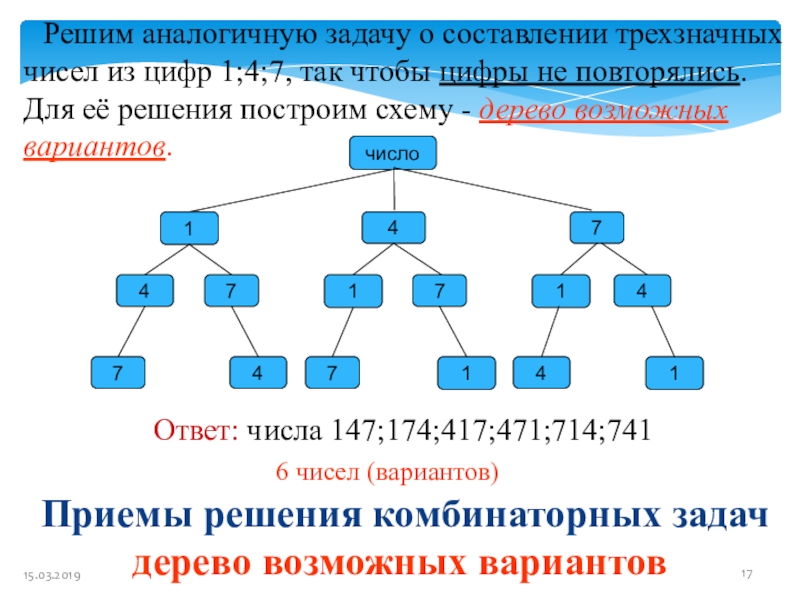
Слайд 17 Приемы решения комбинаторных задач дерево возможных вариантов
Решим аналогичную
число
1
4
7
4
4
7
7
1
1
7
7
1
1
4
4
Ответ: числа 147;174;417;471;714;741
6 чисел (вариантов)
Слайд 18
Заметим, что ответ на вопрос, можно получить, не выписывая
Первую цифру можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать двумя способами. Остается приписать одну цифру. Следовательно, общее число искомых трехзначных чисел равно произведению
Слайд 19 Правило умножения, иначе называемое правилом «и» — одно из основных правил комбинаторики.
Мы нашли ответ на вопрос, используя так называемое комбинаторное правило умножения
Слайд 20 Решите задачу, используя
дерево возможных вариантов
В класс пришли четыре новых
В
С
М
К
Слайд 22 С помощью дерева возможных вариантов решите задачу №714.
Котлеты
Рассольник
Борщ
Обед
Пельмени
Сосиски
Котлеты
Гуляш
Пельмени
Сосиски
Слайд 24Задачи на закрепление
С помощью дерева возможных вариантов решите задачу №714.
№ 717,720
№728
Слайд 25Примеры каких задач были рассмотрены сегодня на уроке?
Какими способами научились решать
Сформулируйте комбинаторное правило умножения?
Слайд 26Домашнее задание:
п. 30 (комбинаторное правило умножения)
№ 716 (перебор), 720 (дерево), 727
Решить № 731 (на повторение)