для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды»
П.Л.Чебышев
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Нахождение наибольшего и наименьшего значения функции на отрезке
Содержание
- 1. Нахождение наибольшего и наименьшего значения функции на отрезке
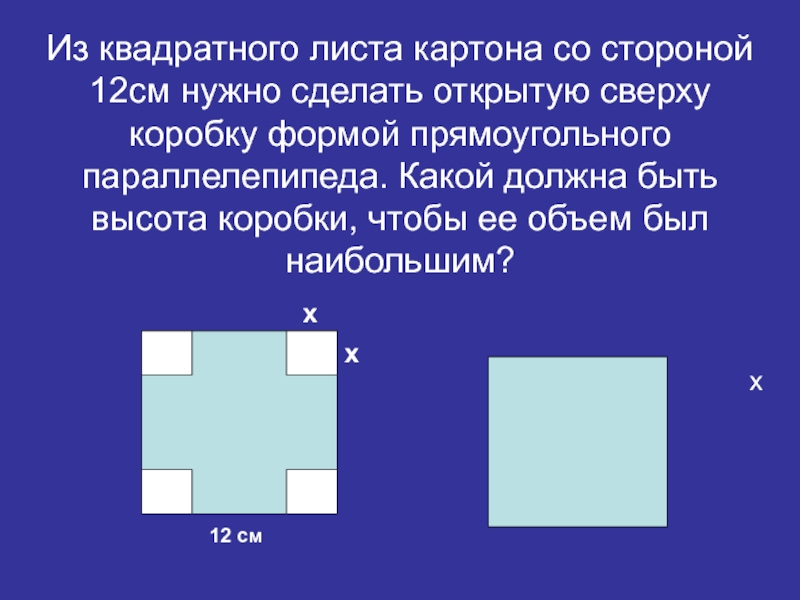
- 2. Из квадратного листа картона со стороной 12см
- 3. Слайд 3
- 4. Найдите наибольшее и наименьшеезначение функции f(x)=x4-8x2+5на отрезке [-1; 2] ?
- 5. Найти y=f’(x).Найти критические точки функции y=f(x) и
- 6. Найдитенаибольшее и наименьшеезначение функцииf(x)=x4-8x2+5на отрезке [-1; 2]
- 7. Найти y=f’(x).Найти критические точки функции y=f(x) и
- 8. Исследовать функцию f(x)=2x3+3x2- 4 на наибольшее и
- 9. Решение: D(f)=R, f ’(x)=5x4-20x3+15x2, D(f ’)=R,f ’(x)=0
- 10. Исследовать функцию y= f(x) на наибольшее и наименьшее значение на отрезке… f наиб=f(1)=0f наим=f(2)=-3f наиб=f(-2)=3f наим=f(-1)=0fнаиб=f(П/2)=2Пfнаим=f(0)=-1fнаиб=f(0)=-1fнаим=f(-П/2)=-2П
- 11. Найти y=f’(x).Найти критические точки функции y=f(x) и
- 12. Домашнее задание:
Из квадратного листа картона со стороной 12см нужно сделать открытую сверху коробку формой прямоугольного параллелепипеда. Какой должна быть высота коробки, чтобы ее объем был наибольшим?
Слайд 2Из квадратного листа картона со стороной 12см нужно сделать открытую сверху
коробку формой прямоугольного параллелепипеда. Какой должна быть высота коробки, чтобы ее объем был наибольшим?
![Найдите наибольшее и наименьшеезначение функции f(x)=x4-8x2+5на отрезке [-1; 2] ?](/img/thumbs/9fb855e067d21a503c79afe6d7e87c8a-800x.jpg "Нахождение наибольшего и наименьшего значения функции на отрезке Найдите наибольшее и наименьшеезначение функции f(x)=x4-8x2+5на отрезке [-1; 2] ?")
Слайд 5Найти y=f’(x).
Найти критические точки функции y=f(x) и выбрать те, которые принадлежат
данному отрезку .
Вычислить значения функции на концах отрезка и в критических точках, принадлежащих отрезку [a;b].
Вычислить значения функции на концах отрезка и в критических точках, принадлежащих отрезку [a;b].
Наибольшее и наименьшее значения функции
Алгоритм нахождения наибольшего и наименьшего значения функции y=f(x) на отрезке [a;b]:
![Найдитенаибольшее и наименьшеезначение функцииf(x)=x4-8x2+5на отрезке [-1; 2]](/img/thumbs/4f132ce65a650000e71b1a35ca7fc9a0-800x.jpg "Нахождение наибольшего и наименьшего значения функции на отрезке Найдитенаибольшее и наименьшеезначение функцииf(x)=x4-8x2+5на отрезке [-1; 2]")
Слайд 7Найти y=f’(x).
Найти критические точки функции y=f(x) и выбрать те, которые принадлежат
данному отрезку .
Вычислить значения функции на концах отрезка и в критических точках, принадлежащих отрезку [a;b].
Вычислить значения функции на концах отрезка и в критических точках, принадлежащих отрезку [a;b].
Алгоритм нахождения наибольшего и наименьшего значения функции y=f(x) на отрезке [a;b]:
Слайд 8Исследовать функцию f(x)=2x3+3x2- 4 на наибольшее и наименьшее значение на отрезке…
Решение: D(f)=R, f ’(x)= 6x2+6x, D(f ’)=R, f ’(x)=0 при x=-1; 0
f наиб=1
f наим=-8
f наиб=-3
f наим=-8
f наиб=24
f наим=-4
f наиб=77
f наим=1
f(-2)=-8
f(-1)=-3
f(0)=-4
f(1)=1
f(-2)=-8
f(-1)=-3
f(-0,5)=-3,5
f(-0,5)=-3,5
f(0)=-4
f(2)=24
f(1)=1
f(3)=77
Слайд 9Решение: D(f)=R, f ’(x)=5x4-20x3+15x2, D(f ’)=R,
f ’(x)=0 при x=0; 1; 3
f
наиб=-3
f наим=-12
f наим=-12
f наиб=-3
f наим=-15
f наиб=60
f наим=-31
f наиб=-3
f наим=-31
Исследовать функцию f(x)=x5-5x4+5x3- 4 на наибольшее и наименьшее значение на отрезке…
f(1)=-3
f(2)=-12
f(-1)=-15
f(0)=-4
f(1)=-3
f(2)=-12
f(3)=-31
f(4)=60
f(0)=-4
f(1)=-3
f(3)=-31
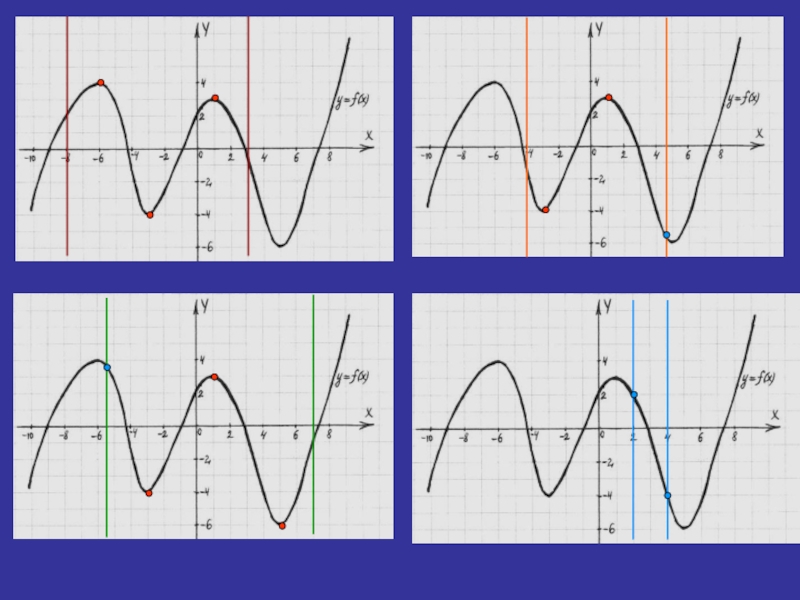
Слайд 10Исследовать функцию y= f(x) на наибольшее и наименьшее значение на отрезке…
f наиб=f(1)=0
f наим=f(2)=-3
f наиб=f(-2)=3
f наим=f(-1)=0
fнаиб=f(П/2)=2П
fнаим=f(0)=-1
fнаиб=f(0)=-1
fнаим=f(-П/2)=-2П
Слайд 11Найти y=f’(x).
Найти критические точки функции y=f(x) и выбрать те, которые принадлежат
данному отрезку .
Вычислить значения функции на концах отрезка и в критических точках, принадлежащих отрезку [a;b].
Вычислить значения функции на концах отрезка и в критических точках, принадлежащих отрезку [a;b].
Алгоритм нахождения наибольшего и наименьшего значения функции y=f(x) на отрезке [a;b]:
