- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Множества.( углубленное изучение математики) 8 класс
Содержание
- 1. Множества.( углубленное изучение математики) 8 класс
- 2. КАНТОР (Cantor) Георг (1845-1918), немецкий математик.
- 3. Рассмотрим несколько примеров множеств. Скрипка, альт, виолончель, контрабас, флейта, фагот, труба, литавры – оркестр..
- 4. Рассмотрим несколько примеров множеств.Кофейник, молочник, сахарница, чашки, блюдца – сервиз.
- 5. Рассмотрим несколько примеров множеств.- натуральные числа.
- 6. Рассмотрим несколько примеров множеств.Для пастуха каждая корова
- 7. Вообще, человеческому мышлению свойственно трактовать то или
- 8. Множество – основное неопределяемое понятие: совокупность, собрание, набор, ансамбль и т. д .
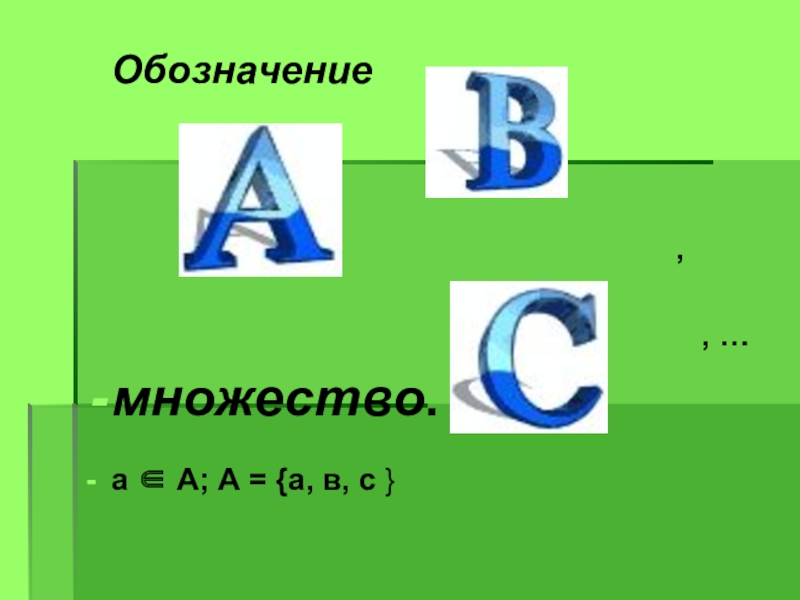
- 9. Обозначение
- 10. Русское слово «множество» может ввести в заблуждение: оно неявно подразумевает некоторое изобилие. Много!
- 11. Но математический термин «множество» этого оттенка совсем
- 12. может состоять из одного элемента – единичное множество (множество естественных спутников Земли),
- 13. может не содержать ни одного элемента –
- 14. Адам и Ева – множество первых людей на земле(согласно библейской легенде).
- 15. Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон множество планет Солнечной системы.
- 16. Андрей Болконский, Пьер Безухов, Наташа Ростова, Николай
- 17. Замечание. Множество персонажей романа в принципе можно
- 18. .Множество можно задать с помощью характеристического (
- 19. Давайте сыграем в слова. Вполне подойдёт слово
- 20. Говорят, что некоторое множество включается в другое,
- 21. {ж, е, м, а, н, с, т,
- 22. В таком случае множества равны{ж, е, м,
- 23. Например: А - множество равносторонних треугольников. В - множество равноугольных треугольников. А = В
- 24. Эйлер Леонард Родился 4 апреля 1707 г., г.
- 25. В математике рисунки в виде кругов, изображающих
- 26. Затем этот метод довольно основательно развил швейцарский
- 27. После Эйлера этот же метод разрабатывал чешский
- 28. Методом кругов Эйлера пользовался и немецкий математик
- 29. Применение кругов Эйлера придает задачам алгебры наглядность
- 30. К Лене на день рождения пришли гости
- 31. Слайд 31
- 32. На лужайке расположились 10 крокодилов. Крокодилов в
- 33. В коробке было 10 круглых или шоколадных
- 34. Миша, Коля, Лева вместе прочитали 3 книги.
- 35. Из 110 студентов английский язык изучают 44
- 36. А U В – объединение множествА и
- 37. А∩В есть множество всех предметов, являющихся элементами
- 38. Два множества называются непересекающимися или расчлененными), если выполняется
- 39. Ā- дополнение множества А Это множество{ х
- 40. Каждый пятый среди исполнителей рок - музыки
- 41. В некотором царстве
- 42. Комната площадью 12м2 покрыта тремя коврами. Площадь
- 43. Известно, что верны следующие утверждения:среди людей, имеющих
- 44. В комнате несколько человек. Каждый из них
- 45. 85% делегатов конференции знают английский язык, 75%
- 46. Отец передал своим детям записки. Коля прочитал:
- 47. Два родных брата, Карп и Поликарп, получили
- 48. В следующей четверти новая темаТы готов?
КАНТОР (Cantor) Георг (1845-1918), немецкий математик. Разработал основы теории множеств, оказавшей большое влияние на развитие математики
Слайд 2
КАНТОР (Cantor) Георг
(1845-1918), немецкий математик.
Разработал основы теории множеств,
оказавшей
большое влияние на развитие
математики
математики
Слайд 3Рассмотрим несколько примеров множеств.
Скрипка, альт, виолончель, контрабас, флейта, фагот, труба,
литавры – оркестр.
.
Слайд 4Рассмотрим несколько примеров множеств.
Кофейник, молочник, сахарница, чашки, блюдца – сервиз.
Слайд 6Рассмотрим несколько примеров множеств.
Для пастуха каждая корова – особая, со своим
характером и привычками.
Для постороннего – это просто стадо.
Для постороннего – это просто стадо.
Слайд 7Вообще, человеческому мышлению свойственно трактовать то или иное собрание предметов, родственных
по какому-либо признаку, как самостоятельный объект.
Слайд 8Множество – основное неопределяемое понятие: совокупность, собрание, набор, ансамбль и т.
д .
Слайд 10Русское слово «множество» может ввести в заблуждение: оно неявно подразумевает некоторое
изобилие. Много!
Слайд 11Но математический термин «множество» этого оттенка совсем не имеет. Множество может
состоять из двух элементов (множество естественных спутников Марса – Фобос и Деймос),
Слайд 12может состоять из одного элемента – единичное множество (множество естественных спутников
Земли),
Слайд 13может не содержать ни одного элемента – пустое множество (множество владельцев
вечного двигателя, множество квадратных колёс, множество острых шаров, множество кривых прямых).
Обозначение пустого множества .
Обозначение пустого множества .
Слайд 15Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон
множество
планет Солнечной системы.
Слайд 16Андрей Болконский, Пьер Безухов, Наташа Ростова, Николай Ростов, Анатоль Курагин и
т.д. - множество персонажей романа Л.Н.Толстого «Война и мир».
Слайд 17Замечание. Множество персонажей романа в принципе можно было бы определить перечислением
( в нашем примере - несколько страниц книги), а вот для натуральных чисел такой пример не годится, поскольку их множество бесконечно.
Слайд 18.Множество можно задать с помощью характеристического ( определяющего ) свойства, такого,
что им обладает каждый элемент этого множества и не обладает ни один предмет, который этому множеству не принадлежит.
Например:
Множество действительных чисел
между 0 и 1.
Определение окружности.
Например:
Множество действительных чисел
между 0 и 1.
Определение окружности.
Слайд 19Давайте сыграем в слова. Вполне подойдёт слово «множества». Вспомним игру: «Из
большого слова - маленькие слова».
нож, нос, сон, стон, жена, манеж, жетон, монета, жеманство
и т.д.
Любой элемент каждого нового множества букв принадлежит исходному буквенному множеству.
Слайд 20Говорят, что некоторое множество включается в другое, если каждый элемент первого
множества является также элементом другого.
При этом первое множество называется подмножеством
(или частью) второго.
{н, о, ж} {м, н, о, ж, е, с, т, в, а}
Слайд 21{ж, е, м, а, н, с, т, в, о} {м,
н, о, ж, е, с, т, в, а}
{м, н, о, ж, е, с, т, в, а} {ж, е, м, а, н, с, т, в, о}
Наша самая большая удача - данная анаграмма.
{м, н, о, ж, е, с, т, в, а} {ж, е, м, а, н, с, т, в, о}
Наша самая большая удача - данная анаграмма.
Слайд 23Например:
А - множество равносторонних треугольников.
В - множество равноугольных треугольников.
А = В
Слайд 24Эйлер Леонард Родился 4 апреля 1707 г., г. Базель, Германия. Математик, механик, физик. Адъюнкт по физиологии,
профессор физики, профессор высшей математики.
Слайд 25В математике рисунки в виде кругов, изображающих множества, используются очень давно.
Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 - 1716). В его черновых набросках были обнаружены рисунки с такими кругами.
Слайд 26Затем этот метод довольно основательно развил швейцарский математик Леонард Эйлер (1707
- 1783). Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые "Письма к немецкой принцессе", написанные в период с 1761 по 1768 год. В некоторых из этих "Писем..." Эйлер как раз и рассказывает о своем методе.
Слайд 27После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781
- 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы.
Слайд 28Методом кругов Эйлера пользовался и немецкий математик Эрнест Шредер (1841 -
1902). Этот метод широко используется в книге "Алгебра логики". Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 - 1923). С наибольшей полнотой этот метод изложен им в книге "Символическая логика", изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера-Венна.
Слайд 29Применение кругов Эйлера придает задачам алгебры наглядность и простоту. Круги Эйлера
с успехом применяются также в логических задачах для изображения множеств истинности высказываний и во многих других случаях. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Данная тема, безусловно расширяет математический кругозор учащихся, обогащает арсенал средств, используемых в решении разнообразных задач.
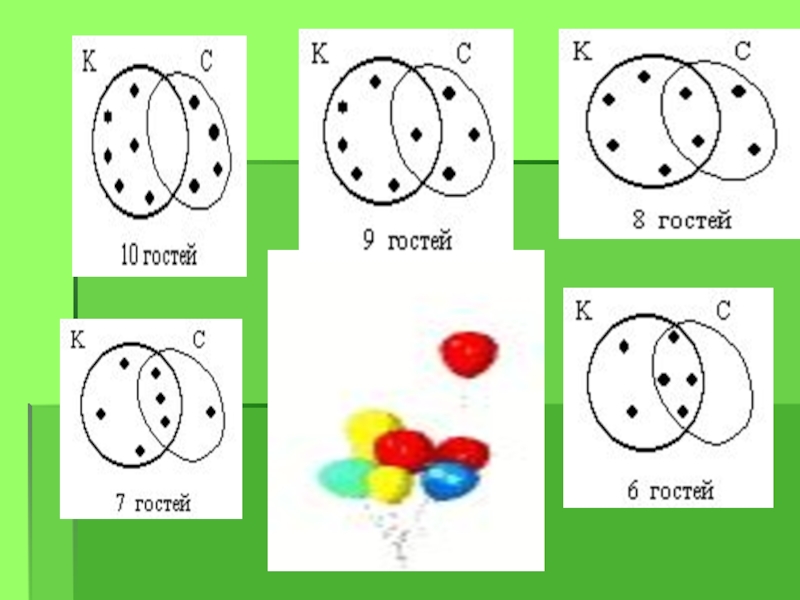
Слайд 30К Лене на день рождения пришли гости с подарками. Получилось так,
что дарили только букеты цветов и воздушные шарики. Шесть гостей подарили букеты цветов, четыре – воздушные шарики. Сколько было гостей?
Слайд 32На лужайке расположились 10 крокодилов.
Крокодилов в галстуке было 6,
а
4 крокодила были больны. Сколько было
на лужайке здоровых крокодилов без галстука?
на лужайке здоровых крокодилов без галстука?
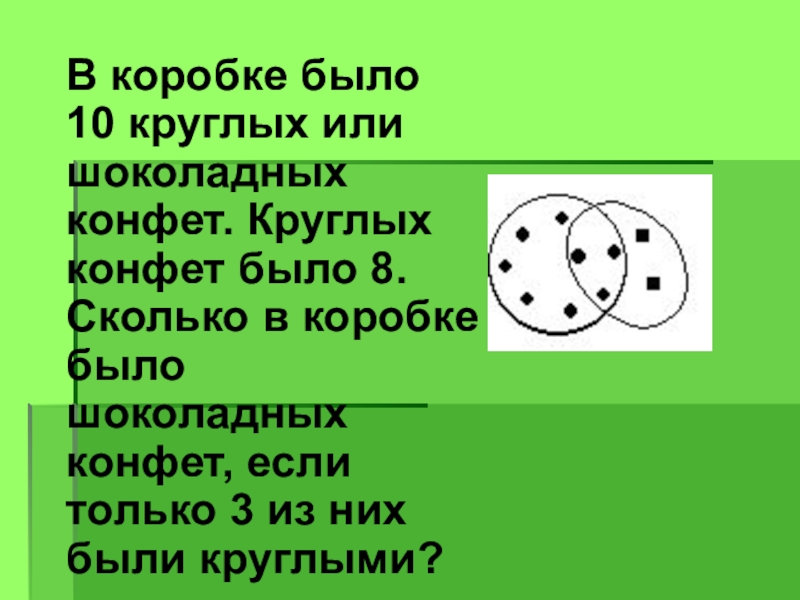
Слайд 33В коробке было 10 круглых или шоколадных конфет. Круглых конфет было
8. Сколько в коробке было шоколадных конфет, если только 3 из них были круглыми?
Слайд 34Миша, Коля, Лева вместе прочитали 3 книги. Миша и Коля вместе
прочитали 5 книг; Миша и Лева вместе – 4 книги; Коля и Лева вместе – 3 книги. Миша прочитал 8 книг; Коля – 6 книг; Лева – 5 книг. Сколько книг прочитали дети?
Слайд 35Из 110 студентов английский язык изучают 44 человека, немецкий – 50
человек, французский – 49 человек, английский и немецкий – 13, английский и французский – 14, немецкий и французский – 12, все три языка изучают 5 человек. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?
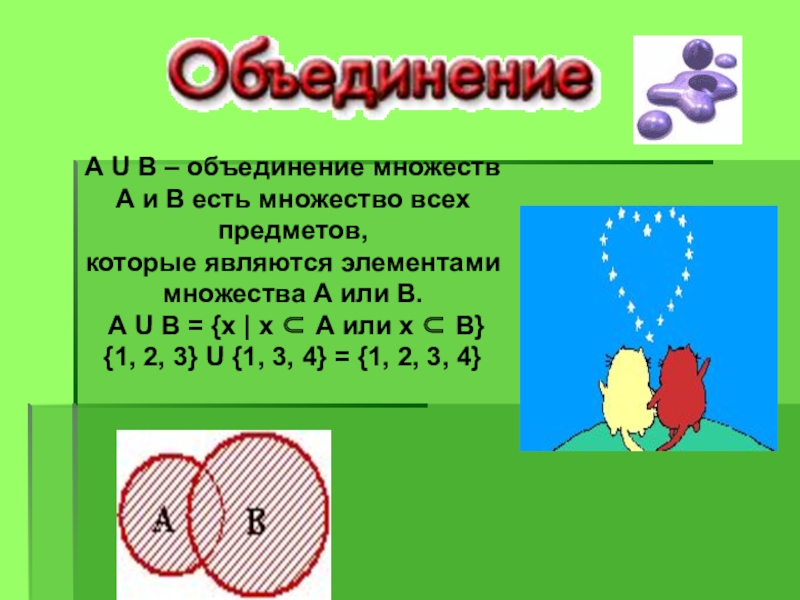
Слайд 36А U В – объединение множеств
А и В есть множество всех
предметов,
которые являются элементами множества А или В.
А U В = {х | х А или х В}
{1, 2, 3} U {1, 3, 4} = {1, 2, 3, 4}
которые являются элементами множества А или В.
А U В = {х | х А или х В}
{1, 2, 3} U {1, 3, 4} = {1, 2, 3, 4}
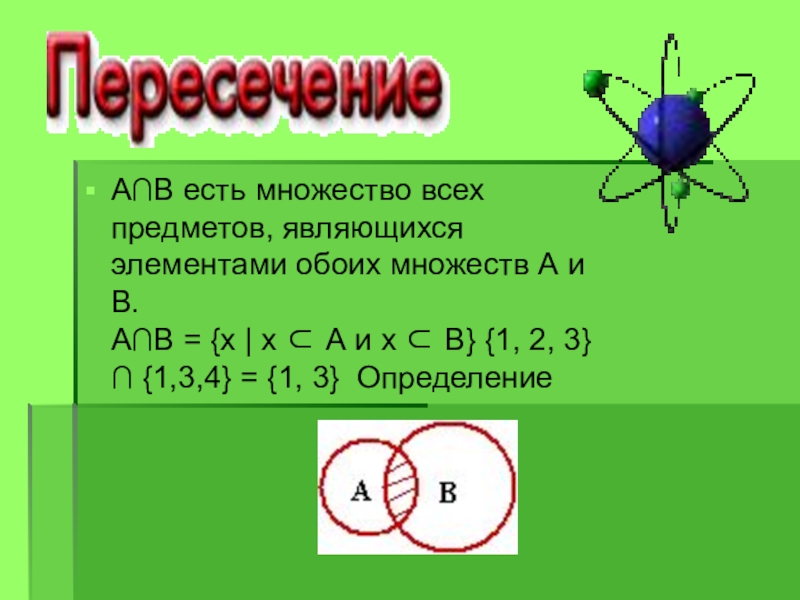
Слайд 37А∩В есть множество всех предметов, являющихся элементами обоих множеств А и
В.
А∩В = {х | х А и х В} {1, 2, 3} ∩ {1,3,4} = {1, 3} Определение
Слайд 38Два множества называются непересекающимися
или расчлененными),
если выполняется условие А ∩ В
= Ø
и пересекающимися, если - А ∩ В ≠ Ø.
и пересекающимися, если - А ∩ В ≠ Ø.
Слайд 39Ā- дополнение множества А
Это множество{ х | х А}
Дополнение
множества А до множества Х
Это множество Х А или Х-А (Х минус А)
АХ
Равенство А=В
АХ
Равенство А=В
Слайд 40Каждый пятый среди исполнителей рок - музыки знаком с нотами. Каждый
седьмой из тех, кто знает ноты, исполняет рок-музыку. Кого больше: рок - музыкантов или людей, знакомых с нотами?
Слайд 41 В некотором царстве
живут маги, чародеи
и колдуны. Про них известно следующее:
не все маги являются чародеями
если колдун не является чародеем, то он не маг.
Правда ли, что не все маги - колдуны?
Слайд 42Комната площадью 12м2 покрыта тремя коврами. Площадь первого ковра 5м2, второго
- 4м2, третьего - 3м2. Каждые два ковра перекрываются на площади 1,5м2, причем 0,5м2 из этих 1,5м2 закрыты всеми тремя коврами. Найдите площадь пола
а) не покрытую коврами;
б) покрытую лишь первым ковром.
Слайд 43Известно, что верны следующие утверждения:
среди людей, имеющих телевизоры, есть такие, которые
не являются малярами
люди, каждый день купающиеся в бассейне, но не являющиеся малярами, не имеют телевизоров.
Следует ли отсюда, что не все владельцы телевизоров каждый день купаются в бассейне
люди, каждый день купающиеся в бассейне, но не являющиеся малярами, не имеют телевизоров.
Следует ли отсюда, что не все владельцы телевизоров каждый день купаются в бассейне
Слайд 44В комнате несколько человек. Каждый из них знает хотя бы один
из трех языков. Шесть человек знают английский язык, шесть - немецкий, семь - французский. Четверо знают английский и немецкий, трое - немецкий и французский, двое - французский и английский. Один человек знает все три языка.
Сколько человек в комнате? Сколько из них знают только английский?
Сколько человек в комнате? Сколько из них знают только английский?
Слайд 4585% делегатов конференции знают английский язык, 75% испанский. Какая часть делегатов
наверняка знает оба эти языка?
Слайд 46Отец передал своим детям записки. Коля прочитал: “Если к моим деньгам
прибавить половину их, то получится 81 рубль. Сколько у меня денег?” Шура прочитала: “Если мама положит в свой кошелек еще треть денег, находящихся в нем, то получится 68 рублей. Сколько денег в кошельке?” Помогите детям решить задачу.
Слайд 47Два родных брата, Карп и Поликарп, получили в наследство 240 рублей.
Карп и говорит Поликарпу: “Дай мне из своей доли 25 рублей и я стану вдвое богаче тебя.” “ Нашел простачка, ”- подумал Поликарп и не дал ему 25 рублей. Сколько денег досталось каждому из братьев?