- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка раздела учебной программы по алгебре
Содержание
- 1. Методическая разработка раздела учебной программы по алгебре
- 2. Алгебра 8 классПрограмма - Алимов Ш. А.
- 3. Пояснительная запискаУравнения в школьном курсе алгебры занимают
- 4. Формировать умение решать квадратные
- 5. Задачи изучения разделаПроводить доказательные рассуждения о корнях
- 6. Ожидаемые результаты освоения раздела «Квадратные уравнения» учебной
- 7. Ожидаемые результаты освоения раздела «Квадратные уравнения» учебной
- 8. Ожидаемые результаты освоения раздела «Квадратные уравнения» учебной
- 9. Обоснование образовательных технологий, методов, форм организации деятельности обучающихся Информационно-коммуникационные технологии Технологии проблемного обучения Здоровьесберегающие технологии
- 10. Методы обучения по источнику получения знаний Словесные Объяснение Эвристическая беседаНаглядные Метод иллюстраций КомпьютерПрактическиеУпражнения Устные Воспроизводящие Тренировочные
- 11. Методы обучения в зависимости от характера познавательной деятельности обучающихсяОбъяснительно-иллюстративный Проблемный Частично-поисковый метод
- 12. Формы организации учебной деятельности обучающихся Фронтальная форма Индивидуальная форма Групповая форма
- 13. Принципы организации учебной деятельности Принцип научности Принцип
- 14. Формы контроля знаний, умений, навыков Устный опросКарточки Самостоятельная работа Тестовые задания Контрольная работа
- 15. Спасибо за внимание !
- 16. Использование ИКТ в преподавании математикиПодготовка печатных дидактических
- 17. Использую презентации на уроках: Объяснение новой темы. Работа
- 18. Найдите квадратные уравнения:2х - 5х + 3
- 19. Таблица тренажер
- 20. Необходимость решать уравнения не только первой, но
- 21. Правило решения этих уравнений, изложенное в
- 22. Франсуа Виет
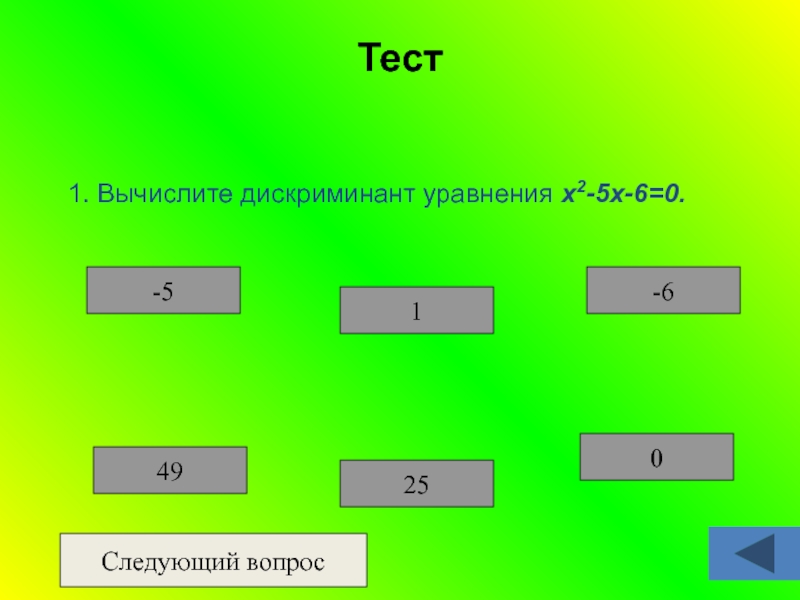
- 23. Тест1. Вычислите дискриминант уравнения х2-5х-6=0.0-6125-549Следующий вопрос
- 24. 2. Сколько корней имеет уравнение, если D < 0?Три корняОдин кореньДва корняКорней не имеетСледующий вопрос
- 25. 3. Выберите корни уравнения 2у2-9у+10=0.у1=-2; у2=-2,5Корней не имеету1=2; у2=-2,5у1=2; у2=2,5
- 26. 8) Решите уравнение:
- 27. 8) Решите уравнение:
- 28. 10) Замените равносильным приведенным квадратным уравнением уравнение:
- 29. 11)Представьте, если возможно, в виде квадрата двучлена:
- 30. 14) Составьте выражение по условию задачи:
- 31. Алгоритм решения квадратного уравнения:ах²+вх+с=0Определить коэффициенты а,в,сЕсли D0, то1 кореньУравнение не имеет корней
- 32. Примеры решения квадратных уравнений по формулеПример1: 3х²+11х+6=0
- 33. Тест 3Квадратные уравненияВариант 1ЧАСТЬ 1А1. Найдите сумму
- 34. Урок – игра «Крестики – нолики»
- 35. Конкурс «Эрудит».
- 36. Конкурс «Помоги другу». 1. Какие уравнения называются биквадратными.2. Сколько корней может иметь биквадратное уравнение.3. Решить уравнения.
- 37. Конкурс «SOS».
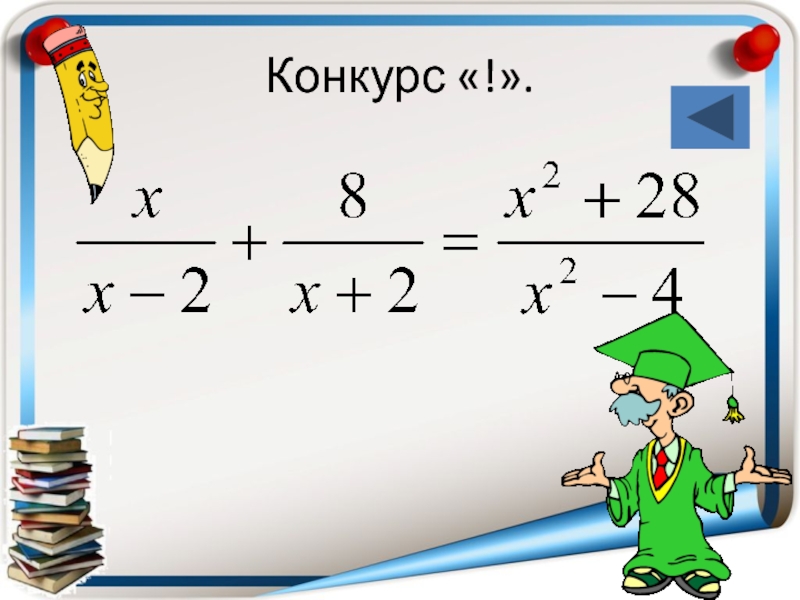
- 38. Конкурс «!».
- 39. Эстафетах2 = 3 х2 + х =
- 40. Самостоятельная работа1вариант2 вариант1. Сумма корней квадратного уравнения
- 41. Разноуровневые индивидуальные карточки
- 42. Нечётные партыЧётные парты1. Найти корни приведённых квадратных
- 43. Уравнения умнее своих создателейГенрих Гейц3. Мяч брошен
- 44. Самостоятельная работа 4.1Квадратное уравнение и его корни
- 45. Разноуровневая контрольная работаУровень 1 1. Решите уравнения:
- 46. Физкультминутка
Слайд 1Методическая разработка
раздела учебной программы
по алгебре 8 класс
тема:
«Квадратные уравнения»
Учитель
МБОУ «Вадская СОШ»
Москвичева В. И.
Слайд 2Алгебра 8 класс
Программа - Алимов Ш. А. и др.
Программы по
М.: Просвещение, 2008
Учебник - Алимов Ш. А. и др.
Алгебра.- М.: Просвещение, 2009
Слайд 3Пояснительная записка
Уравнения в школьном курсе алгебры занимают ведущее место. На их
Слайд 4 Формировать умение
решать квадратные
уравнения различными
способами;
решать уравнения,
сводящиеся к
квадратным,
выполнять проверку
решенного уравнения;
Формировать умение
решать задачи с
помощью
квадратных уравнений
Развивать логическое
и алгоритмическое
мышление;
Развивать
интеллектуальные
и творческие
способности
обучающихся,
интереса к изучению
математики;
Развивать умение
сравнивать, выявлять,
обобщать
закономерности.
Цели изучения раздела
Воспитание качеств
личности,
формируемых в
ходе учебной
математической
деятельности и
обеспечивающих
социальную
мобильность,
творческую ,
активность,
способность
принимать
самостоятельные
решения.
Слайд 5Задачи изучения раздела
Проводить доказательные рассуждения
о корнях уравнения с опорой на
корня, функциональные свойства выражений
Решать текстовые задачи алгебраическим
способом:
переходить от словесной формулировки
условия задачи к алгебраической модели
путем составления уравнения;
решать составленное уравнение
Слайд 6Ожидаемые результаты освоения раздела «Квадратные уравнения» учебной программы по алгебре для
В результате изучения раздела «Квадратные уравнения »
обучающиеся должны
Знать:
Определение квадратного уравнения;
Различать полные и неполные, приведенные и неприведенные
квадратные уравнения;
Формулу корней квадратного уравнения;
Различные алгоритмы решения квадратных уравнений,
а так же алгоритм решения задач
с помощью квадратных уравнений
Понимать
Что уравнения – это математический аппарат решения
разнообразных задач из математики,
смежных областей знаний, практики;
Слайд 7Ожидаемые результаты освоения раздела «Квадратные уравнения» учебной программы по алгебре для
В результате изучения раздела «Квадратные уравнения »
обучающиеся должны
Уметь
Составлять квадратное уравнение, если заданы коэффициенты:
Решать квадратные уравнения и рациональные уравнения,
сводящиеся к ним различными способами,
простейшие системы, содержащие уравнения
второй степени;
Решать текстовые задачи алгебраическим методом,
интерпретировать полученный результат,
проводить отбор решений, исходя из формулировки задачи;
Слайд 8Ожидаемые результаты освоения раздела «Квадратные уравнения» учебной программы по алгебре для
В результате изучения раздела «Квадратные уравнения »
обучающиеся должны
Научиться:
Выполнять расчеты по формулам, составлять формулы,
выражающие зависимости между реальными величинами;
Моделировать практические ситуации и исследовать
построенные модели ;
Планировать и осуществлять алгоритмическую деятельность,
выполнять заданные и конструировать новые алгоритмы;
Видеть применение изучаемого материала в практической
деятельности;
Систематизировать, анализировать и классифицировать
информацию, использовать разнообразие
информационных источников, включая учебную
и справочную литературу, современные
информационные технологии.
Слайд 9Обоснование образовательных технологий, методов, форм организации деятельности обучающихся
Информационно-коммуникационные технологии
Технологии
Здоровьесберегающие технологии
Слайд 10Методы обучения по источнику
получения знаний
Словесные
Объяснение
Эвристическая
беседа
Наглядные
Метод
иллюстраций
Компьютер
Практические
Упражнения
Устные
Воспроизводящие
Тренировочные
Слайд 11Методы обучения в зависимости
от характера
познавательной
деятельности обучающихся
Объяснительно-иллюстративный
Проблемный
Частично-поисковый
Слайд 12Формы организации учебной деятельности обучающихся
Фронтальная форма
Индивидуальная форма
Групповая форма
Слайд 13Принципы организации учебной деятельности
Принцип научности
Принцип системности
Принцип доступности
Принцип
Принцип сознательности и активности
Принцип прочности формируемых знаний
Принцип учёта индивидуальности
обучающихся
Слайд 14Формы контроля знаний,
умений, навыков
Устный опрос
Карточки
Самостоятельная работа
Тестовые задания
Контрольная работа
Слайд 16Использование ИКТ в преподавании математики
Подготовка печатных дидактических материалов
Создание компьютерных презентаций
Использование
для поиска информации исторического,
практического характера
Применение компьютерных тестов
для контроля ЗУН обучающихся
Слайд 17Использую презентации на уроках:
Объяснение новой темы.
Работа с устными упражнениями.
Использование презентации
пройденного материала.
Демонстрация условия и решения задачи.
Взаимопроверка самостоятельных работ
с помощью ответов на слайде.
Проведение тестов.
Проведение физкультминуток
Слайд 18Найдите квадратные уравнения:
2х - 5х + 3 = 0
х + 3х
5х = 0
2
2
2
7х - 10 = 0
2
12х – 24 = 0
- х + 4 х = 0
2
9х - 6х + 1 = 0
2
3х + 5 = 0
8х + 10х = 0
2
х - 25 = 0
2
Слайд 20Необходимость решать уравнения не только первой, но и второй степени ёщё
Квадратные уравнения в Древнем Вавилоне.
Немного из истории
Слайд 21
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с
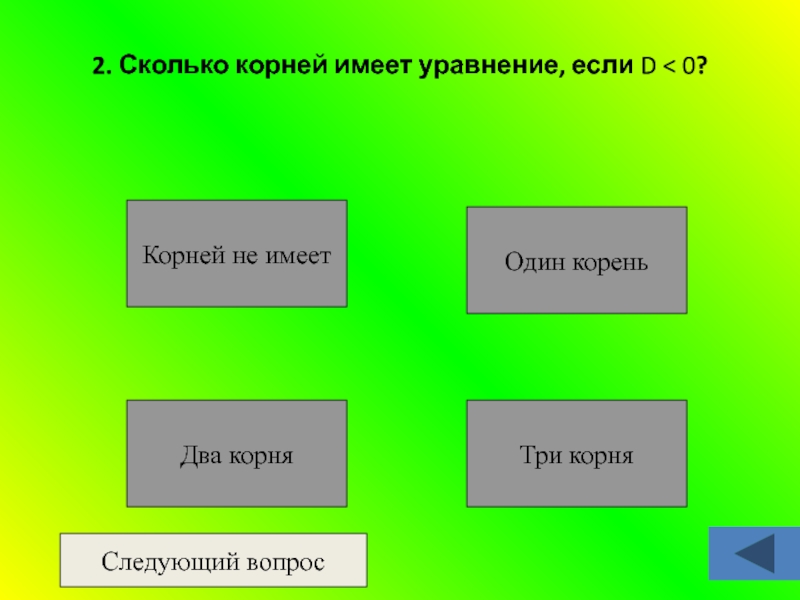
Слайд 242. Сколько корней имеет уравнение, если D < 0?
Три корня
Один корень
Два
Корней не имеет
Следующий вопрос
Слайд 253. Выберите корни уравнения 2у2-9у+10=0.
у1=-2; у2=-2,5
Корней не имеет
у1=2; у2=-2,5
у1=2; у2=2,5
Слайд 3014) Составьте выражение по условию задачи: а) найти периметр прямоугольника, если его
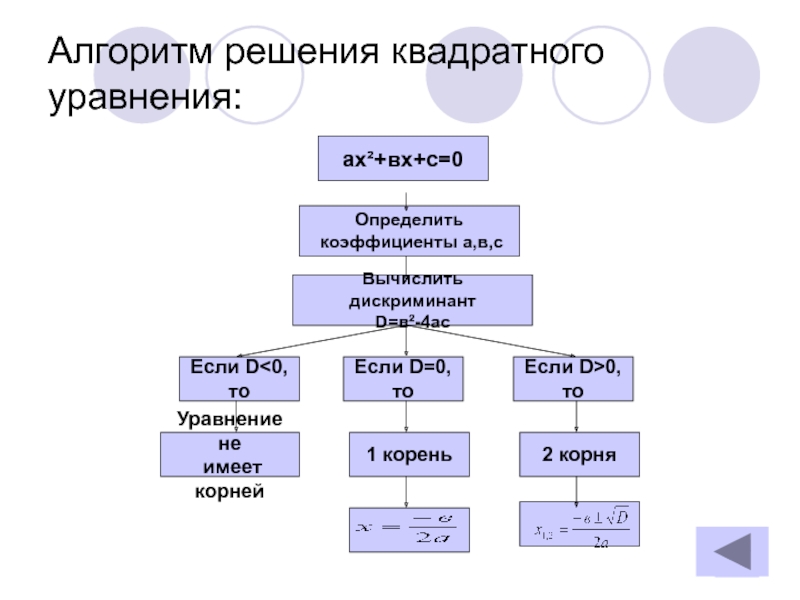
Слайд 31Алгоритм решения квадратного уравнения:
ах²+вх+с=0
Определить
коэффициенты а,в,с
Если D
Если D>0, то
1 корень
Уравнение не
имеет корней
Слайд 32Примеры решения квадратных уравнений по формуле
Пример1: 3х²+11х+6=0
а=3;
D=11²-4*3*6=121-72=49 >0 – уравнение имеет 2 корня
Слайд 33Тест 3
Квадратные уравнения
Вариант 1
ЧАСТЬ 1
А1. Найдите сумму корней уравнения:
А2. Найдите произведение корней уравнения:
1) -0,5 2) 1 3) 0,5 4) 5
А3. Найдите произведение корней уравнения:
1) -14 2) 7 3) -7 4) 4
А4. Сколько действительных корней имеет уравнение
1) 1 2) 2 3) 3 4) ни одного
А5. Сколько действительных корней имеет уравнение
1) 4 2) 2 3) 3 4) ни одного
А6. Сколько действительных корней имеет уравнение
1) 3 2) 2 3) 1 4) ни одного.
А7. Найдите значение коэффициента а, если в уравнении
один из корней уравнения равен -1.
1) -14 2) -12 3) -2 4) -1
Слайд 36Конкурс «Помоги другу».
1. Какие уравнения называются биквадратными.
2. Сколько корней может
3. Решить уравнения.
Слайд 39Эстафета
х2 = 3
х2 + х = 0
3х2 + 6 =
х2+ 5х + 4 = 0
3х2 = 0
9х2 – 1 = 0
х2 = 7
х2 + 3х = 0
2х2 + 4 = 0
х2 – 3х + 2 = 0
5х2 = 0
1 - 4х2 = 0
1. х1,2 =
+
2. х1 = 0, х2 = -1
3. Корней нет
4. х1 = -4, х2 = -1
5. х = 0
6. х1,2 =
+
-
1. х1,2 =
+
-
2. х1 = 0, х2 = -3
3. Корней нет
4. х1 = 2, х2 = 1
5. х = 0
6. х1,2 =
+
-
-
Слайд 40Самостоятельная работа
1вариант
2 вариант
1. Сумма корней квадратного уравнения равна
2. Произведение корней квадратного
3. Сколько действительных корней имеет квадратное уравнение
4. Найдите корни квадратного уравнения
5. Найдите все значения а при которых квадратное уравнение
имеет два различных корня
не имеет корней
-4
-5
2
1; 0,25
-5
3
0
1; 2/3
a <25
a >25
Слайд 41Разноуровневые индивидуальные карточки
1 уровень 2 уровень 3 уровень
4 уровень 5 уровень
Индивидуальная карточка
(для каждого ученика)
Слайд 42Нечётные парты
Чётные парты
1. Найти корни приведённых квадратных уравнений:
1. Записать приведённое квадратное
2. Разложить квадратный трёхчлен на множители:
2. Разложить квадратный трёхчлен на множители:
3. Сократить дробь:
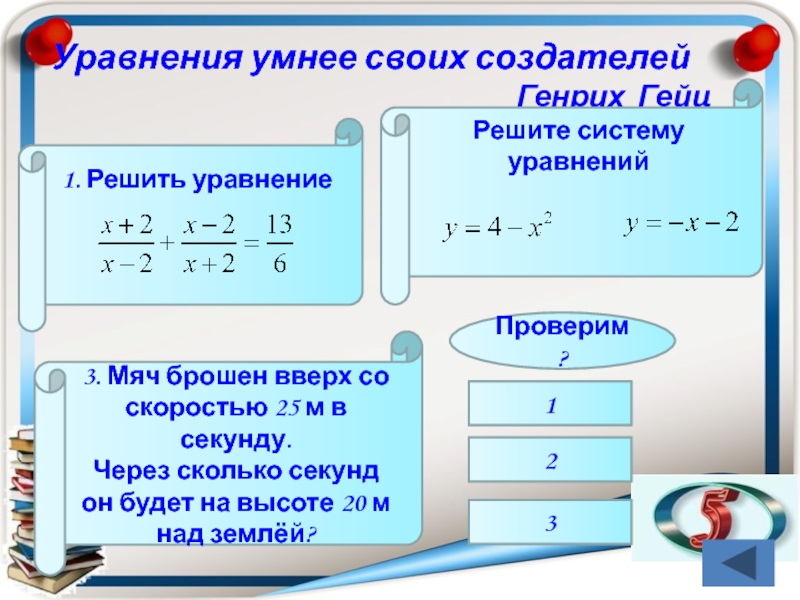
Слайд 43Уравнения умнее своих создателей
Генрих Гейц
3. Мяч брошен вверх со скоростью 25
Через сколько секунд он будет на высоте 20 м над землёй?
Проверим?
(3;-5);(-2;0)
1 сек.; 4 сек
1
2
3
Слайд 44
Самостоятельная работа 4.1
Квадратное уравнение и его корни
Вариант 1
1. Найдите корни
2. Найдите корни уравнения:
3. Решите уравнение:
а) б)
4. Решите уравнение способом выделения квадрата двучлена:
Самостоятельная работа 4.2
Решение квадратных уравнений по формуле
Вариант 1.
1. Решите уравнение:
2.При каких значениях k квадратное уравнение
не имеет корней?
Самостоятельные работы
Слайд 45Разноуровневая контрольная работа
Уровень 1
1. Решите уравнения:
2. При каких
3. Решите уравнение с помощью теоремы,
обратной теореме Виета.
4. Один из корней квадратного уравнения равен 2.
Найдите второй корень и коэффициент а.
Уровень 2
Решите уравнения:
2. При каких значениях х равны значения многочленов
и ?
3. Решите уравнение с помощью теоремы,
обратной теореме Виета.
4. Один из корней квадратного уравнения
в 2 раза больше другого.
Найдите корни уравнения и коэффициент с.