- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка по теме Решение квадратных неравенств
Содержание
- 1. Методическая разработка по теме Решение квадратных неравенств
- 2. Решение квадратных неравенствАлгебра. 8 классУроки 2 - 4*
- 3. Слайд 3
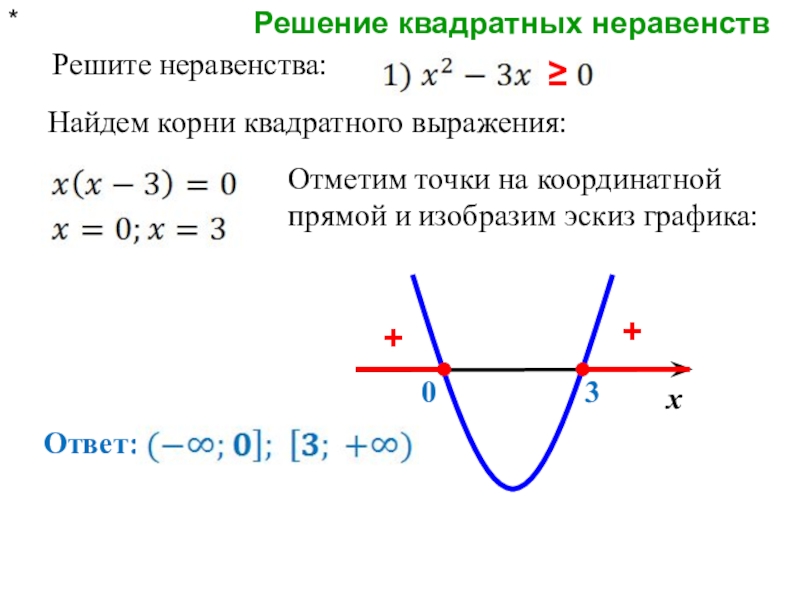
- 4. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного выражения:03≥++Отметим точки на координатной прямой и изобразим эскиз графика:Ответ:х
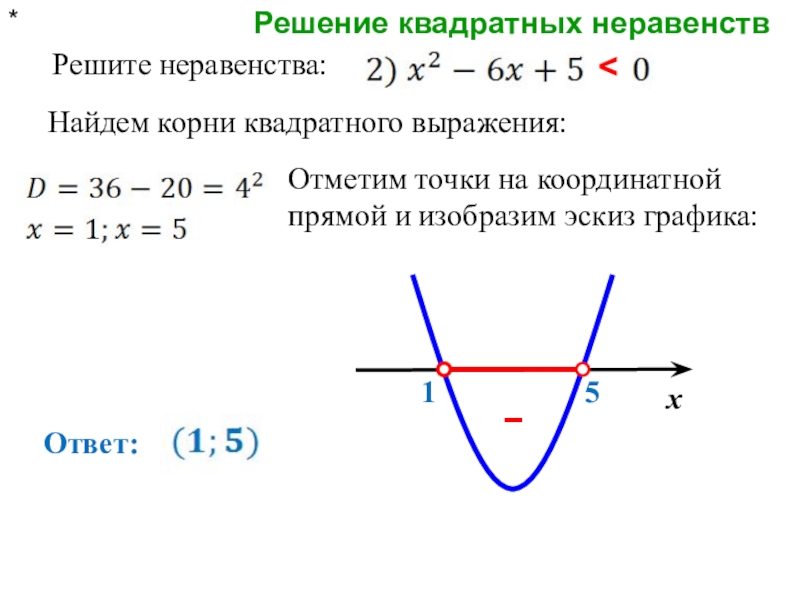
- 5. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного выражения:15
- 6. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного
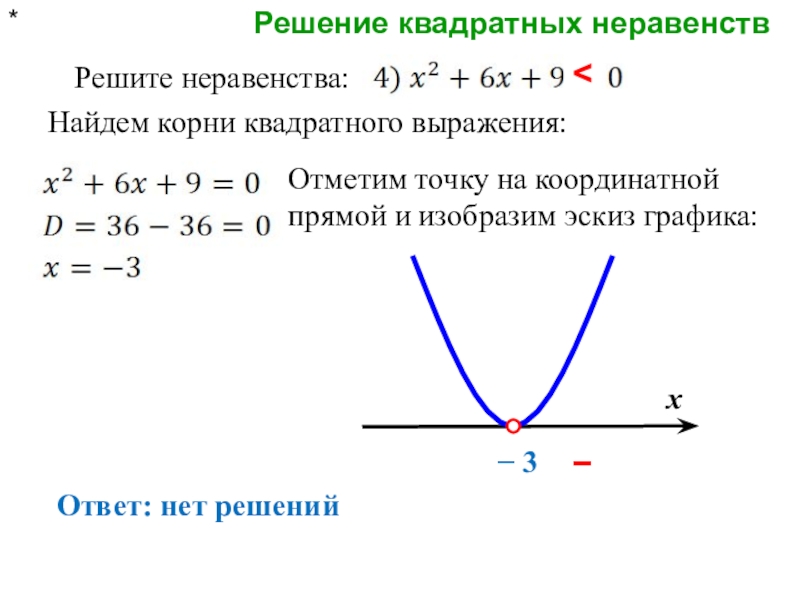
- 7. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного выражения:− 3
- 8. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного
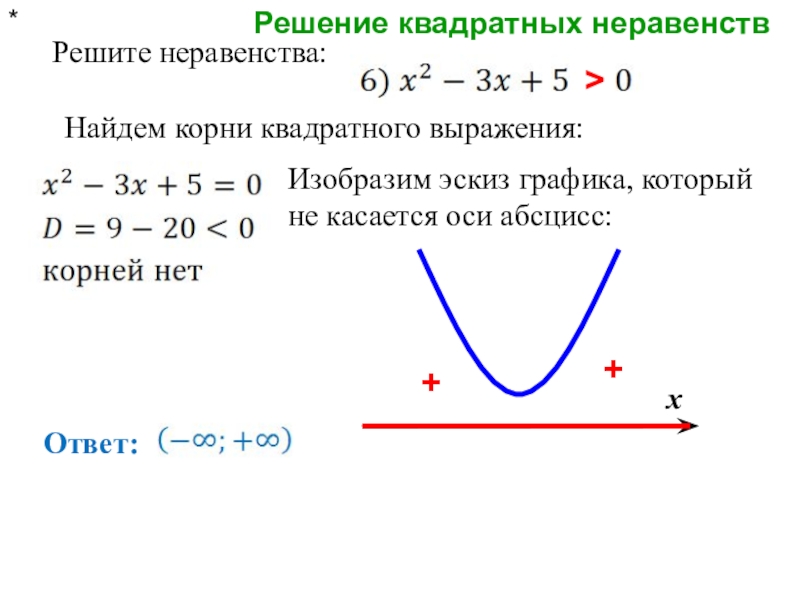
- 9. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного выражения:>++Изобразим эскиз графика, который не касается оси абсцисс:Ответ:х
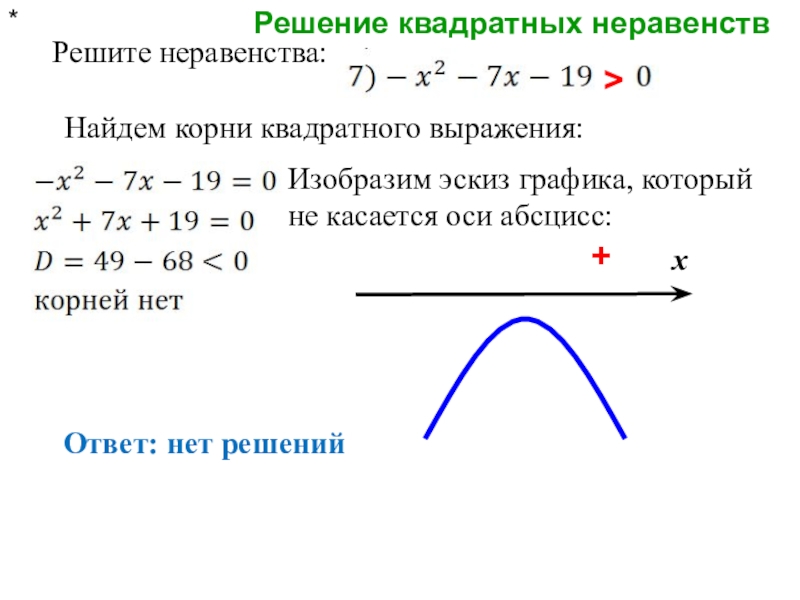
- 10. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного
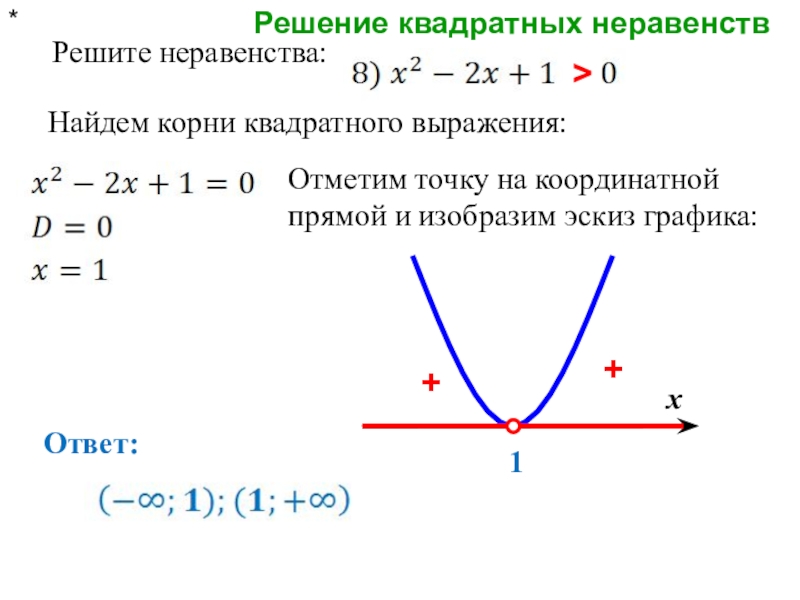
- 11. Решение квадратных неравенств* Решите неравенства:Найдем корни квадратного выражения:1>++Отметим точку на координатной прямой и изобразим эскиз графика:Ответ:х
- 12. Разбираем вместеРешите неравенства: 1) х² + 5х
- 13. Самостоятельно:Решить неравенства 1) х(х +
- 14. Домашнее задание § 41, № 662(2;4); 664(2;4); 667(2;4). Урок закончен.Спасибо за внимание!
- 15. Домашнее задание № 663(2,4), 664(2,4), 666(2,4), 669(2,4)§
- 16. Решение квадратных неравенств* Решите неравенства:СамостоятельноОтветы: 1)2)3)4)5)6)7)8)9)
- 17. Решение квадратных неравенств* Решите неравенства:Ответы: 1)2)3)4)5)
- 18. Решение квадратных неравенств*
- 19. Слайд 19
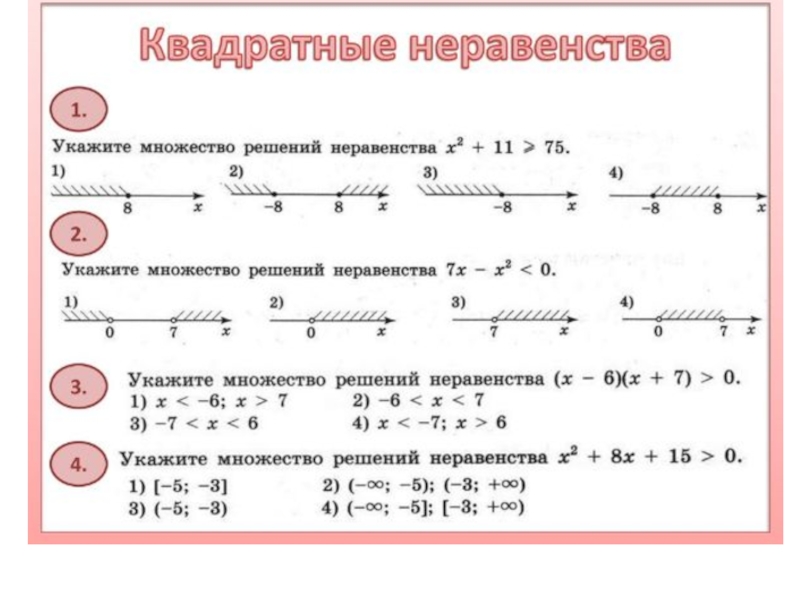
- 20. Решение квадратных неравенств* Решите неравенства:
- 21. Решение квадратных неравенств* При каких положительных значениях
- 22. Решение квадратных неравенств* Решите неравенство x2 − ax + 3 ≤ 0 прн любых значениях a?
- 23. Домашнее задание № 768(2,4), 668(2,4), 667(6,8), 669(6,8) Урок закончен.Спасибо за внимание!
- 24. Решите неравенства:Решение квадратных неравенств*
- 25. Решите неравенства:Решение квадратных неравенств*
- 26. Решите неравенства:Решение квадратных неравенств*
- 27. Решение квадратных неравенств*
- 28. Самостоятельная работа
Слайд 4Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
0
3
≥
+
+
Отметим точки на координатной
Ответ:
х
Слайд 5Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
1
5
Ответ:
х
Слайд 6Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
− 2
≥
+
+
Отметим точку на
Ответ:
х
Слайд 7Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
− 3
Ответ: нет решений
х
Слайд 8Решение квадратных неравенств
*
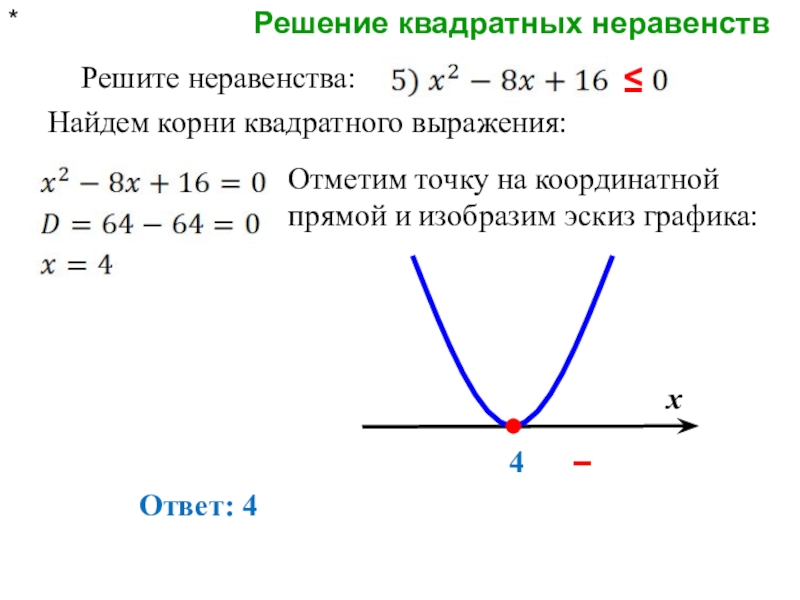
Решите неравенства:
Найдем корни квадратного выражения:
4
≤
−
Отметим точку на координатной
Ответ: 4
х
Слайд 9Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
>
+
+
Изобразим эскиз графика, который
Ответ:
х
Слайд 10Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
>
+
Изобразим эскиз графика, который
Ответ: нет решений
х
Слайд 11Решение квадратных неравенств
*
Решите неравенства:
Найдем корни квадратного выражения:
1
>
+
+
Отметим точку на координатной
Ответ:
х
Слайд 12Разбираем вместе
Решите неравенства:
1) х² + 5х < 0;
2) х²
3) х² + 2х ≥ 0;
4) − 2х² + х + 1 ≤ 0
Проверим ответы:
(0; − 5)
(-∞; 0); (4; +∞)
(-∞; −2]; [0; +∞)
(-∞; - 0,5]; [1; +∞)
Слайд 13
Самостоятельно:
Решить неравенства
1) х(х + 7) ≥ 0;
2) (х
3) х − х² + 2 < 0;
4) − х² − 5х + 6 > 0;
5) х(х + 2) < 15
Проверим ответы:
1) (-∞;-7]U[0; +∞)
2) [-2;1]
3) (-∞;-1)U(2; +∞)
4) (-6;1)
5) (-5;3)
Слайд 15Домашнее задание
№ 663(2,4), 664(2,4), 666(2,4), 669(2,4)
§ 41, № 662(2;4); 664(2;4);
Урок закончен.
Спасибо
за внимание!
Слайд 21Решение квадратных неравенств
*
При каких положительных значениях x верно неравенство x2
Найдите решения неравенства 0,6x2 ≤ 0,5 − 1,3 x, принадлежащих интервалу [0,25; 1].