- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему МАтериалы для учителя: Комбинаторика для великих комбинаторов
Содержание
- 1. МАтериалы для учителя: Комбинаторика для великих комбинаторов
- 2. Комбинаторика для великих комбинаторов
- 3. Кого из литературных героев называют Великим комбинатором?
- 4. Остап Бендер — это главный герой романов
- 5. Оста́п Бе́ндер — главный герой романов Ильи Ильфа и Евгения Петрова «Двенадцать
- 6. Почему Остапа Бендера называют Великим комбинатором?
- 7. КомбинаторикаТермин «комбинаторика» был введён Лейбницем в 1666
- 8. Перестановки и размещения
- 9. Задача 1. Милиционер плохо запомнил имя преступника,
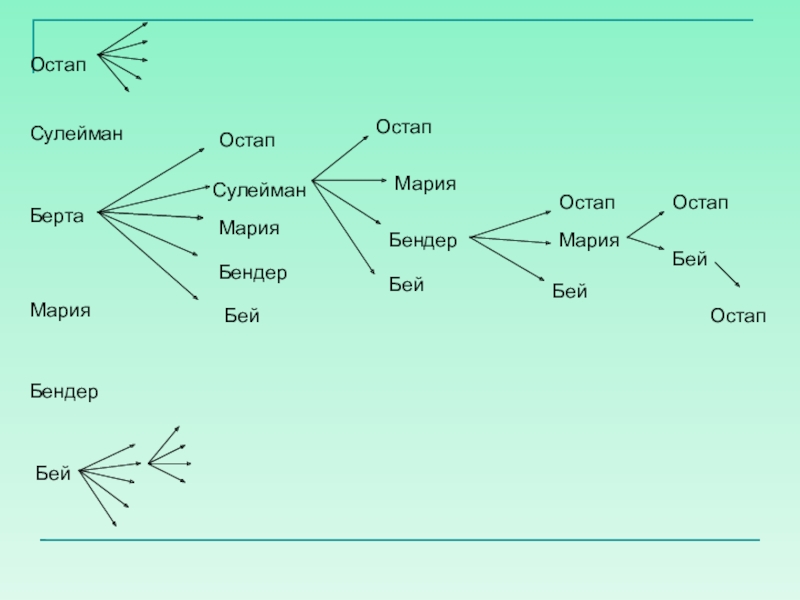
- 10. ОстапСулейманБертаМарияБендерБейОстапСулейманМарияБендерБейОстапМарияБендерБейОстапМарияБейОстапБейОстап
- 11. Слайд 11
- 12. Способы подсчета количества вариантовМетод организованного перебораТаблица (удобно
- 13. Например, организованный переборВ задаче о подбрасывании монеты(О,Р,О)(О,О,О)(О,О,Р)(Р,О,О)И т.д.
- 14. По командам:Яблоко, апельсин, груша и банан лежат
- 15. Слайд 15
- 16. На доске обе команды на скорость таблицейВ
- 17. ЗадачаможетИван ИвановичПетр ИвановичВасилий ИвановичМихаил
- 18. ОстапСулейманБертаМарияБендерБейОстапСулейманМарияБендерБейОстапМарияБендерБейОстапМарияБейОстапБейОстапДерево вариантов
- 19. Ответ к задаче 1.- метод подсчета количества перестановок
- 20. Правило умножения: Если объект a можно
- 21. По командам:Всевозможные размещения из трех элементов 1, 2,
- 22. Слайд 22
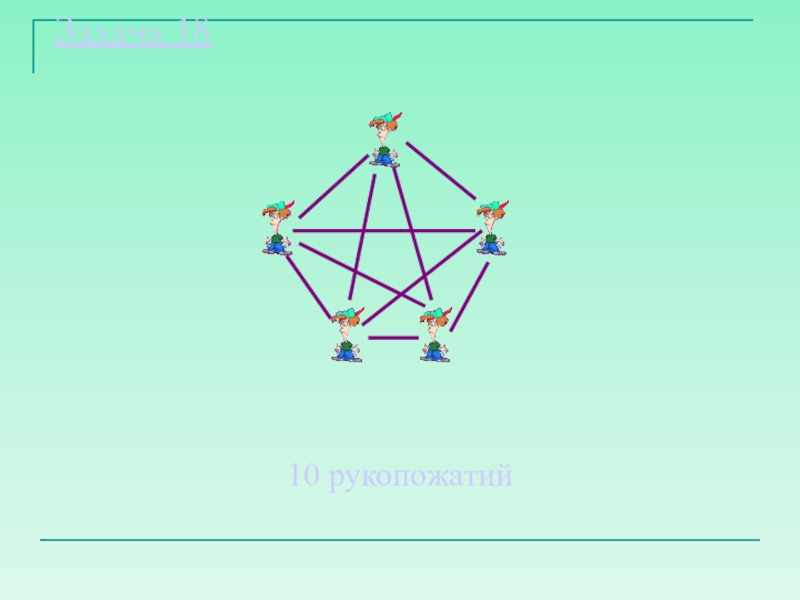
- 23. Задача 18Пятеро друзей встретились после каникул и
- 24. Задача 1810 рукопожатий
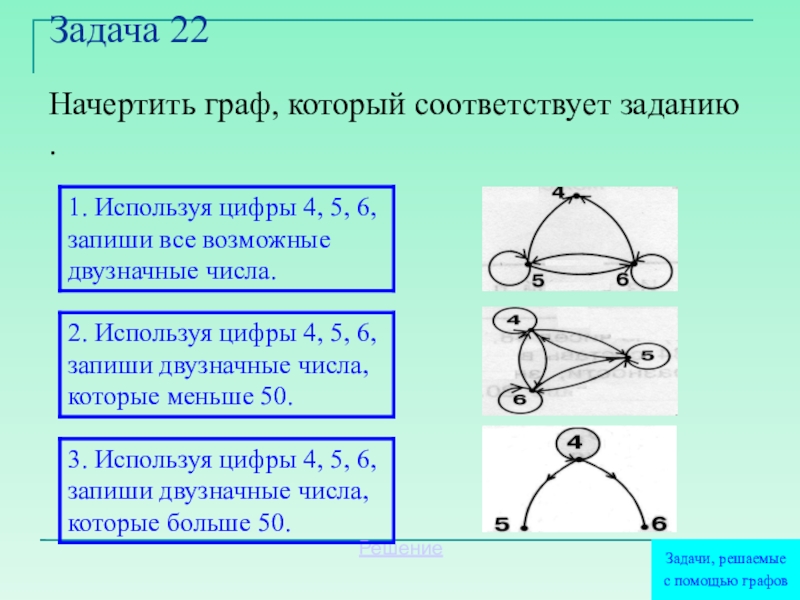
- 25. Задача 22Начертить граф, который соответствует заданию .РешениеЗадачи, решаемыес помощью графов
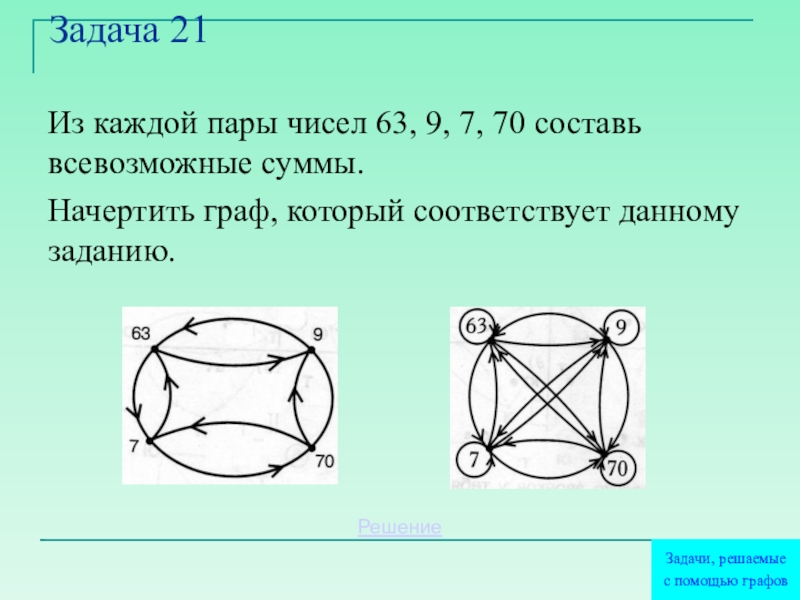
- 26. Задача 21Из каждой пары чисел 63, 9,
- 27. Задача 2 (размещения). Десять стульев были проданы
- 28. Слайд 28
- 29. Сколько стратегий поиска стульев (порядка поиска стульев)
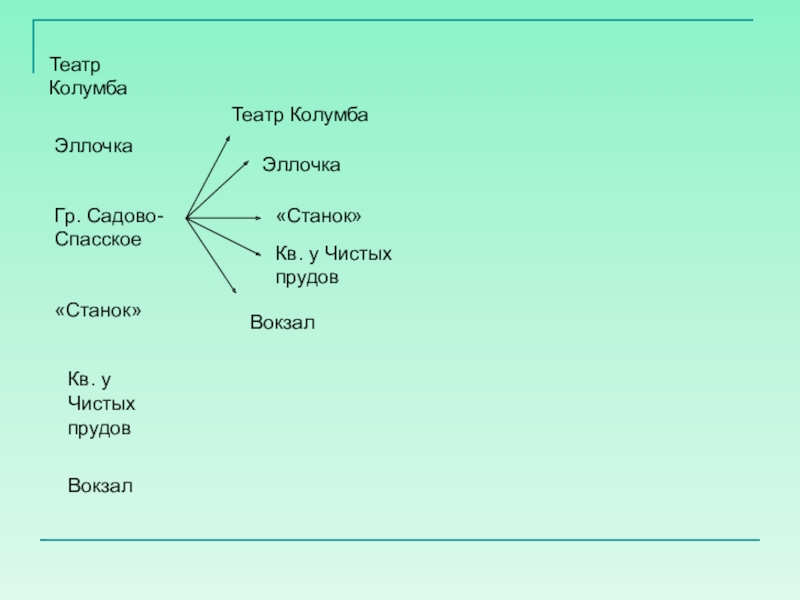
- 30. Театр КолумбаЭллочкаГр. Садово-Спасское«Станок»Кв. у Чистых прудовВокзалТеатр КолумбаЭллочка«Станок»Кв. у Чистых прудовВокзал
- 31. Ответ к задаче 2- вариантов стратегий просчитал Остап Бендер мгновенно.
- 32. Перестановки - комбинации из n элементов, отличающиеся
- 33. Сравнительная таблица подсчета числа перестановок и размещений
- 34. Сочетания
- 35. Задача 3: Членами подпольной организации
- 36. СочетанияКомбинации по m различных элементов, выбранных их
- 37. Задача 3: Членами подпольной организации
- 38. Слайд 38
- 39. Ответ к задаче 3:
- 40. ПерестановкиФормула для подсчета количества всевозможных перестановок:
- 41. РазмещенияФормула для нахождения количества размещений различных m
- 42. Сочетания Формула для нахождения количества сочетаний m элементов из n:
- 43. На занятии мы узнали Для того,
- 44. Вопросы для исследования: Выясните, в каких
- 45. Деловая играМагазин игрушек
- 46. Задача 4. Государственные флаги некоторых стран состоят
- 47. Задача 2. В школьной столовой на завтрак
- 48. По командам:Найти все перестановки цифр числа 1542
- 49. 1. Мастер должен обшить 12 стульев обшивкой
- 50. Спасибо за внимание!
Комбинаторика для великих комбинаторов
Слайд 4Остап Бендер — это главный герой романов Ильи Ильфа и Евгения
Петрова «Двенадцать стульев» и «Золотой телёнок».
Слайд 5Оста́п Бе́ндер — главный герой романов Ильи Ильфа и Евгения Петрова «Двенадцать стульев» и «Золотой телёнок»,
«великий комбинатор», «идейный борец за денежные знаки», знавший «четыреста сравнительно честных способов отъёма (увода) денег». Один из самых популярных героев плутовского романа в отечественной литературе.
Сам Бендер представляется как Остап-Сулейман-Берта-Мария-Бендер-бей (в «Двенадцати стульях») и Бендер-Задунайский (в «Золотом телёнке»). В романе «Золотой телёнок» Бендера именуют Остап Ибрагимович.
Сам Бендер представляется как Остап-Сулейман-Берта-Мария-Бендер-бей (в «Двенадцати стульях») и Бендер-Задунайский (в «Золотом телёнке»). В романе «Золотой телёнок» Бендера именуют Остап Ибрагимович.
Слайд 7Комбинаторика
Термин «комбинаторика» был введён Лейбницем в 1666 году.
Он происходит от латинского
слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Комбинаторика - раздел математики, описывающий методы быстрого подсчета количества различных комбинаций заданных объектов.
Комбинаторика - раздел математики, описывающий методы быстрого подсчета количества различных комбинаций заданных объектов.
Слайд 9Задача 1.
Милиционер плохо запомнил имя преступника, но помнит, что в
нем есть
Мария, Сулейман, Остап, Берта, Бей и Бендер.
Сколько имен должен написать милиционер, чтобы среди них обязательно оказалось имя «преступника»?
Мария, Сулейман, Остап, Берта, Бей и Бендер.
Сколько имен должен написать милиционер, чтобы среди них обязательно оказалось имя «преступника»?
Слайд 10Остап
Сулейман
Берта
Мария
Бендер
Бей
Остап
Сулейман
Мария
Бендер
Бей
Остап
Мария
Бендер
Бей
Остап
Мария
Бей
Остап
Бей
Остап
Слайд 12Способы подсчета количества вариантов
Метод организованного перебора
Таблица (удобно для выбора двух значений
из нескольких возможных)
Дерево вариантов
Граф
Формулы для подсчета количества размещений, перестановок и сочетаний
Дерево вариантов
Граф
Формулы для подсчета количества размещений, перестановок и сочетаний
Слайд 13Например,
организованный перебор
В задаче о подбрасывании монеты
(О,Р,О)
(О,О,О)
(О,О,Р)
(Р,О,О)
И т.д.
Слайд 14По командам:
Яблоко, апельсин, груша и банан лежат на столе в ряд.
Апельсин
не в начале и не в конце этого ряда.
Стоя лицом к этому ряду, можно увидеть, что апельсин - справа от банана (но не обязательно рядом с ним).
Сколько разных вариантов расположения фруктов может быть ?
Стоя лицом к этому ряду, можно увидеть, что апельсин - справа от банана (но не обязательно рядом с ним).
Сколько разных вариантов расположения фруктов может быть ?
Окно в комнате Кости имеет прямоугольную форму и разделено на 3х3 маленьких секций.
Костя хочет покрасить две секции желтой краской. Но он хочет покрасить их так, чтобы окно смотрелось одинаковым, если смотреть на него снаружи или изнутри.
Сколько всего способов покрасить свое окно есть у Кости ?
Слайд 16На доске обе команды на скорость таблицей
В одной деревне по сложившейся
традиции мужчин называют каким-либо из следующих имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин с разными именами. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем и отчеством?
Решение
Решение
Задачи, решаемые
с помощью таблиц
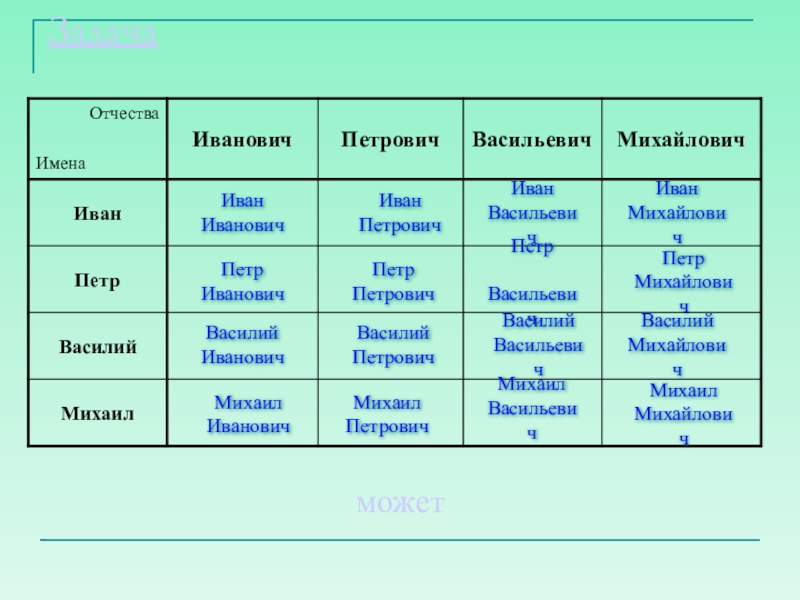
Слайд 17Задача
может
Иван
Иванович
Петр
Иванович
Василий
Иванович
Михаил
Иванович
Иван
Петрович
Петр
Петрович
Василий
Петрович
Михаил
Петрович
Иван
Васильевич
Василий
Васильевич
Петр
Васильевич
Михаил
Васильевич
Иван
Михайлович
Петр
Михайлович
Василий
Михайлович
Михаил
Михайлович
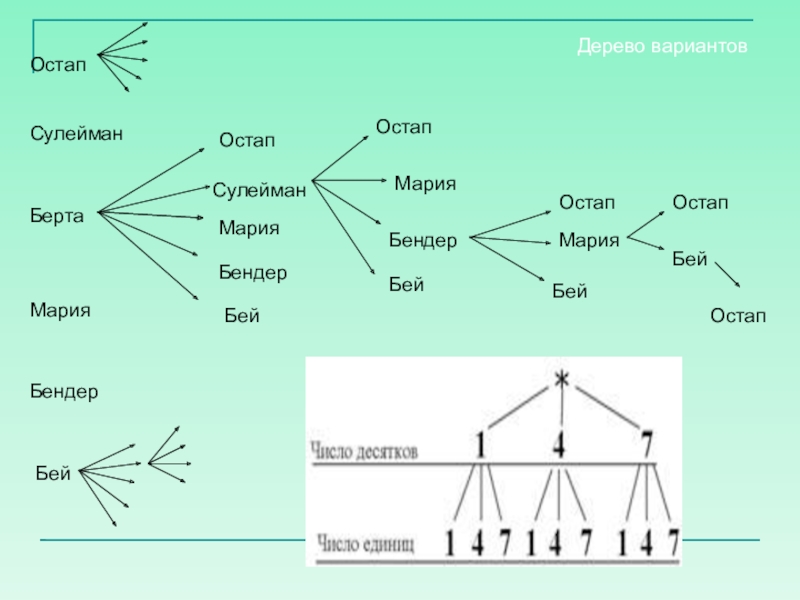
Слайд 18Остап
Сулейман
Берта
Мария
Бендер
Бей
Остап
Сулейман
Мария
Бендер
Бей
Остап
Мария
Бендер
Бей
Остап
Мария
Бей
Остап
Бей
Остап
Дерево вариантов
Слайд 20Правило умножения:
Если объект a можно выбрать m способами, а
объект b можно выбрать k способами, то выбор пары (a, b) можно осуществить
m · k способами.
m · k способами.
Слайд 21По командам:
Всевозможные размещения из трех элементов 1, 2, 3 по два элемента
без повторений:
12, 13, 21, 23, 31, 32.
12, 13, 21, 23, 31, 32.
Всевозможные размещения из трех элементов 1, 2, 3 по два элемента с повторениями:
12, 13, 21, 23, 31, 32, 11, 22, 33
Слайд 23Задача 18
Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь,
пожал руку. Сколько всего было сделано рукопожатий?
Решение
Решение
Задачи, решаемые
с помощью графов
Слайд 25Задача 22
Начертить граф, который соответствует заданию .
Решение
Задачи, решаемые
с помощью графов
Слайд 26Задача 21
Из каждой пары чисел 63, 9, 7, 70 составь всевозможные
суммы.
Начертить граф, который соответствует данному заданию.
Решение
Начертить граф, который соответствует данному заданию.
Решение
Задачи, решаемые
с помощью графов
Слайд 27Задача 2 (размещения).
Десять стульев были проданы с аукциона в розницу.
Остап Бендер отправил по их следу беспризорников. Он узнал:
Слайд 29
Сколько стратегий поиска стульев (порядка поиска стульев) Остап Бендер смог просчитать
мгновенно, если за один миг он просчитывал все варианты развития событий на два шага вперед?
Слайд 30Театр Колумба
Эллочка
Гр. Садово-Спасское
«Станок»
Кв. у Чистых прудов
Вокзал
Театр Колумба
Эллочка
«Станок»
Кв. у Чистых прудов
Вокзал
Слайд 32Перестановки - комбинации из n элементов, отличающиеся друг от друга только
порядком их расположения
Найти все перестановки цифр числа 1542 и 8362 ( на баллы) и их количество
Размещения - комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов
Пример. Всевозможные размещения из трех элементов 123 и 561 по два элемента:12, 13, 21, 23, 31, 32.
А с повторениями + 11, 22, 33
Найти все перестановки цифр числа 1542 и 8362 ( на баллы) и их количество
Размещения - комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов
Пример. Всевозможные размещения из трех элементов 123 и 561 по два элемента:12, 13, 21, 23, 31, 32.
А с повторениями + 11, 22, 33
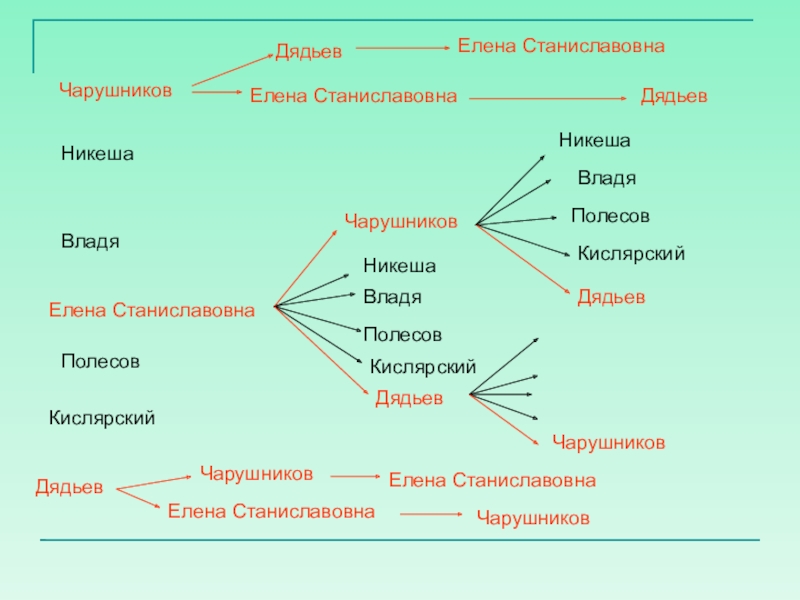
Слайд 35Задача 3: Членами подпольной организации были 7 человек: 1. Чарушников,
2. Никеша,
3. Владя,
4. Полесов,
5. Елена Станиславовна,
6. Кислярский,
7. Дядьев.
Остап устраивал собрания подпольщиков.
На них он приглашал по 3 члена союза.
На каждом собрании Остап Бендер зарабатывал по 1 тысяче рублей.
Сколько денег Остап Бендер сможет собрать с подпольщиков, если будет приглашать на собрания каждый раз новый состав членов подпольной организации?
Слайд 36Сочетания
Комбинации по m различных элементов, выбранных их множества n данных элементов,
которые отличаются друг от друга только составом элементов называются сочетаниями
Слайд 37Задача 3: Членами подпольной организации были 7 человек: 1. Чарушников,
2. Никеша,
3. Владя,
4. Полесов,
5. Елена Станиславовна,
6. Кислярский,
7. Дядьев.
Остап устраивал собрания подпольщиков.
На них он приглашал по 3 члена союза.
На каждом собрании Остап Бендер зарабатывал по 1 тысяче рублей.
Слайд 40Перестановки
Формула для подсчета количества всевозможных перестановок:
Слово «факториал» в переводе с латинского означает «производящий действие».
Перестановками называют комбинации из n элементов, отличающиеся друг от друга только порядком их расположения
Слайд 41Размещения
Формула для нахождения количества размещений различных m элементов из n:
Размещениями называются
комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов.
Слайд 43На занятии мы узнали
Для того, чтобы стать Великим комбинатором
надо уметь быстро просчитывать все варианты развития событий.
В этом нам помогают формулы:
1.
2.
3.
В этом нам помогают формулы:
1.
2.
3.
- Формула подсчета количества сочетаний
- формула подсчета количества размещений
- Формула подсчета количества перестановок
Слайд 44Вопросы для исследования:
Выясните, в каких жизненных ситуациях Вам, вашим
друзьям и близким может пригодится знание формул подсчета количества:
Перестановок;
Размещений;
Сочетаний.
Составьте на основе этих ситуаций задачи на тему «Комбинаторика вокруг нас».
Перестановок;
Размещений;
Сочетаний.
Составьте на основе этих ситуаций задачи на тему «Комбинаторика вокруг нас».
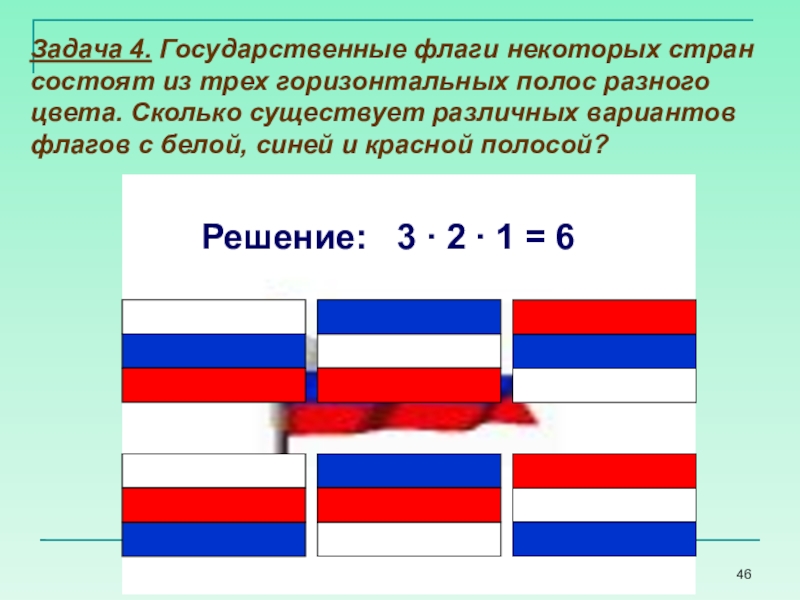
Слайд 46Задача 4. Государственные флаги некоторых стран состоят из трех горизонтальных полос
разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?
Решение: 3 ∙ 2 ∙ 1 = 6
Слайд 47Задача 2. В школьной столовой на завтрак любой ученик может выбрать
булочку, ватрушку или пирожок, а запить их можно соком или чаем. Сколько вариантов завтрака предлагается в школьной столовой?
Решение: 3 · 2 = 6 вариантов завтрака
Сок (С)
Чай (Ч)
Булочка (Б)
Ватрушка (В)
Пирожок (П)
Слайд 48По командам:
Найти
все перестановки цифр числа 1542
и
их количество
Найти
все
перестановки цифр числа 8362
и
их количество
и
их количество
Слайд 491. Мастер должен обшить 12 стульев обшивкой красного, коричневого и зеленого
цвета. Сколькими способами он может это сделать?
Задачи:
Ответ: 12 ∙ 3 = 36
2. Сколькими способами можно выбрать гласную и согласную буквы из слова «правило»?
Ответ: 3 ∙ 4 = 12
3. На первой полке стоит 5 книг, а на второй 10. Сколькими способами можно выбрать одну книгу с первой полки и одну со второй?
Ответ: 5 ∙ 10 = 50
4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Ответ: 9 ∙ 10 ∙ 10 = 900
