нуля (то есть для любого значения из D(f) значение также принадлежит области определения, то проверяем функцию на четность.
Если , то функция четная. Для нас важно, что график четной функции симметричен относительно оси OY.
Если , то функция нечетная. График нечетной функции симметричен относительно начала координат.
Если функция является четной или нечетной, то мы можем построить часть ее графика для, а затем соответствующим образом отразить ее.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Материала для учителя: Производная и дифференциал
Содержание
- 1. Материала для учителя: Производная и дифференциал
- 2. 3. Находим точки пересечения графика с осями координат.Находим
- 3. 6. Если функция периодическая, то находим период функции.7. Исследуем функцию
- 4. 8. Последний этап- точки перегиба и промежутки выпуклости и
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Задание к зачету
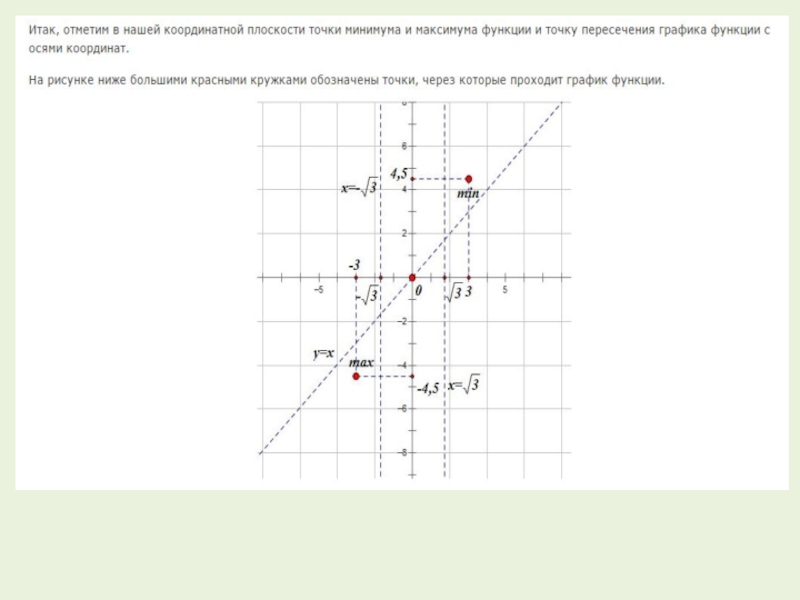
3. Находим точки пересечения графика с осями координат.Находим нули функции - это точки пересечения графика функции с осью абсцисс (OX).Для этого мы решаем уравнение f(x) = 0 .Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ.Находим точку
Слайд 1Алгоритм исследования функции и построения ее графика
1. Находим область определения (D(f)) функции .
2. Если область определения функции симметрична относительно
Слайд 23. Находим точки пересечения графика с осями координат.
Находим нули функции - это
точки пересечения графика функции с осью абсцисс (OX).
Для этого мы решаем уравнение f(x) = 0 .
Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ.
Находим точку пересечения графика функции с осью ординат (OY). Для этого ищем значение функции при x = 0.
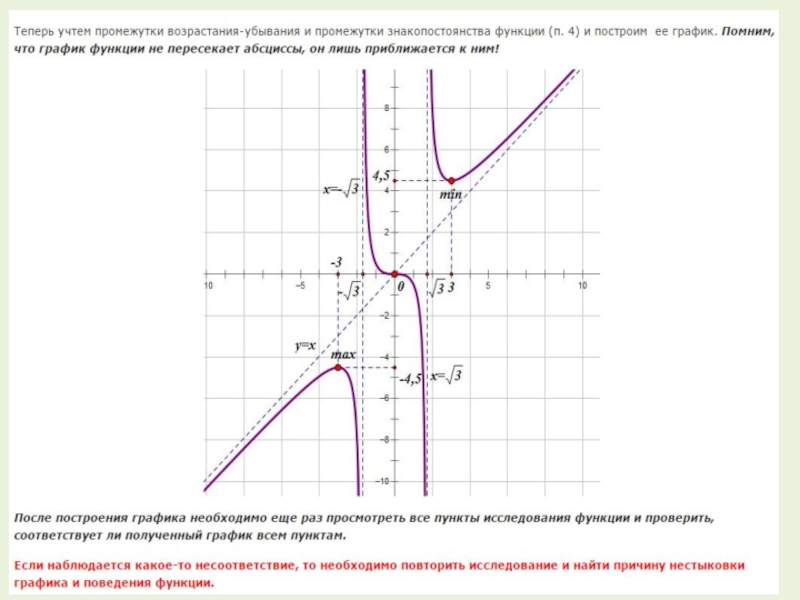
4. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции , нам нужно решить неравенства и .
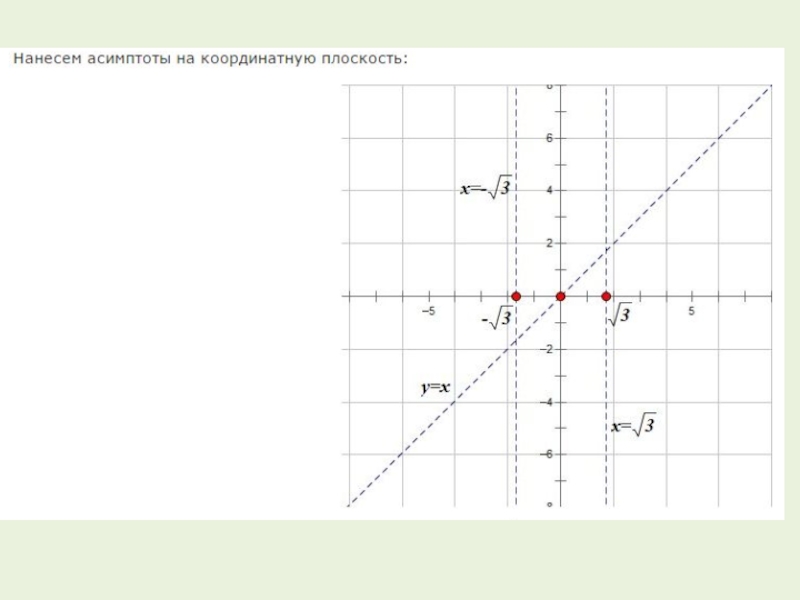
5. Находим асимптоты графика функции.
Как найти асимптоты https://ege-ok.ru/2013/11/12/asimptotyi-grafika-funktsii/
Для этого мы решаем уравнение f(x) = 0 .
Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ.
Находим точку пересечения графика функции с осью ординат (OY). Для этого ищем значение функции при x = 0.
4. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции , нам нужно решить неравенства и .
5. Находим асимптоты графика функции.
Как найти асимптоты https://ege-ok.ru/2013/11/12/asimptotyi-grafika-funktsii/
Слайд 36. Если функция периодическая, то находим период функции.
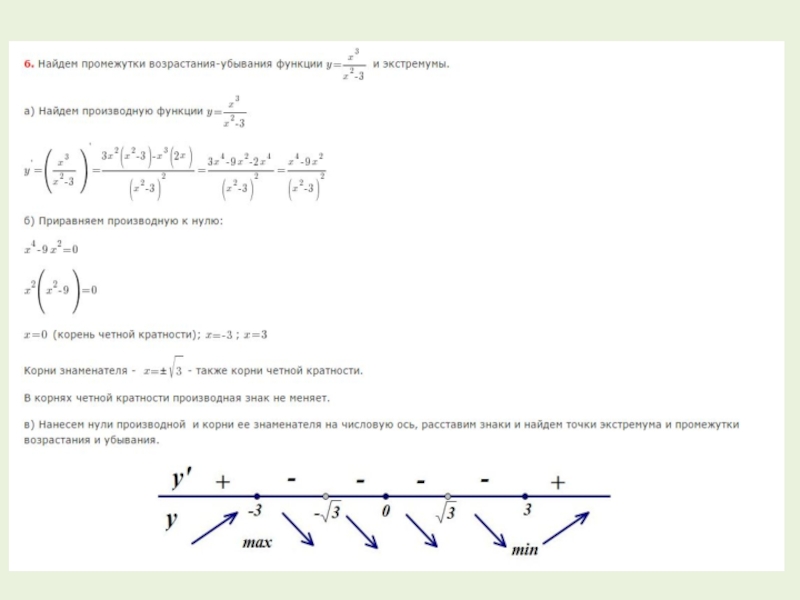
7. Исследуем функцию с помощью производной: находим промежутки
возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную f(x)
б) Приравниваем производную к нулю и находим корни уравнения f’(x) = 0 - это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную f(x)
б) Приравниваем производную к нулю и находим корни уравнения f’(x) = 0 - это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
Слайд 48. Последний этап- точки перегиба и промежутки выпуклости и вогнутости.
Подробнее о том, как находить
точки перегиба и промежутки выпуклости и вогнутости читайте https://ege-ok.ru/2013/11/15/tochki-peregiba-i-promezhutki-vyipuklosti-i-vognutosti-grafika-funktsii/ .