- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мастер-класс Задачи на смеси и сплавы
Содержание
- 1. Мастер-класс Задачи на смеси и сплавы
- 2. Незнающие пусть научатся, знающие –
- 3. Цель: профессиональное самосовершенствование участников мастер-класса
- 4. Чтобы лучше понимать условия задач, необходимо
- 5. типы задач на вычисление концентрации; на вычисление
- 6. Методы решения задачалгебраический, арифметический, графический, способ расчета
- 7. «Правило креста» или «Конверт Пирсона».Задача: «Имеется 30
- 8. Графический метод Задача.
- 9. С помощью формулы:
- 10. Арифметический метод
- 11. Алгебраический метод
- 12. «Метод прямоугольников».40 % 60%0% 100%30% 70%
- 13. «Метод рыбки»
- 14. Метод стаканчиковЗадача. Сколько
- 15. При помощи универсальной таблицы
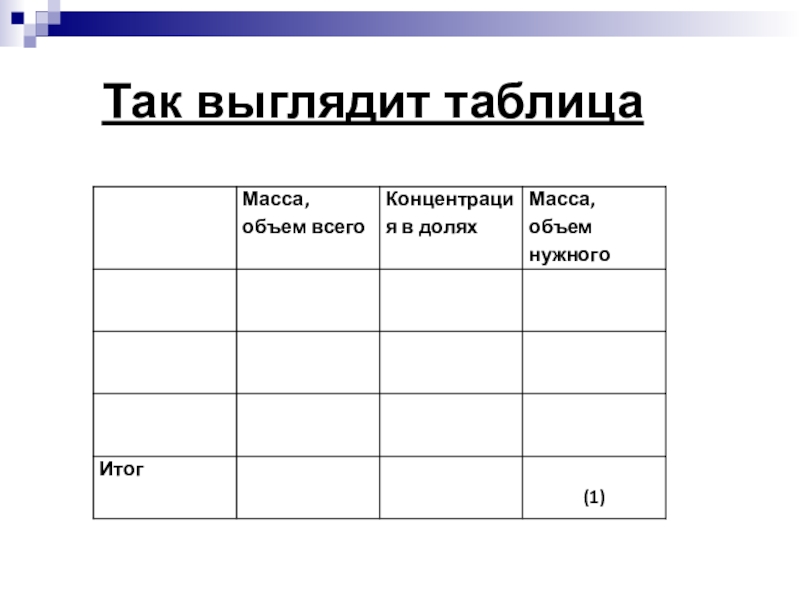
- 16. Так выглядит таблица
- 17. Слайд 17
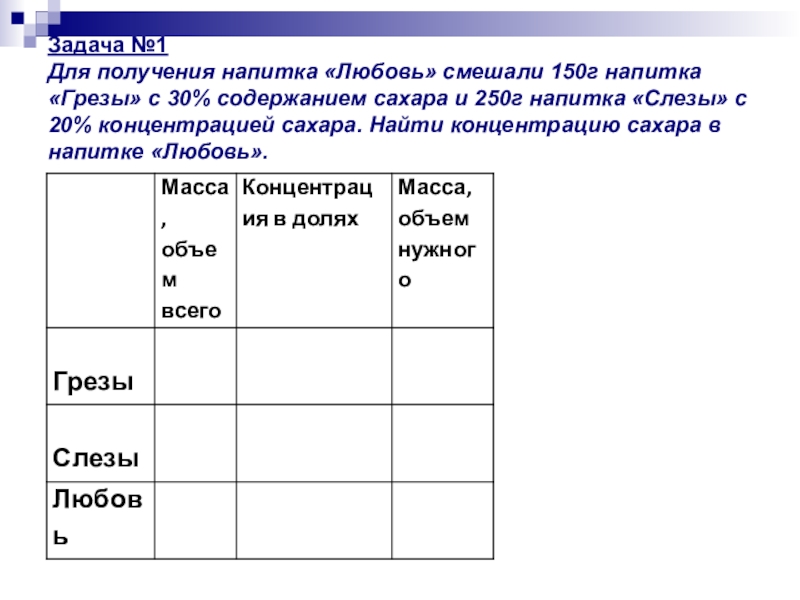
- 18. Задача №1 Для получения напитка
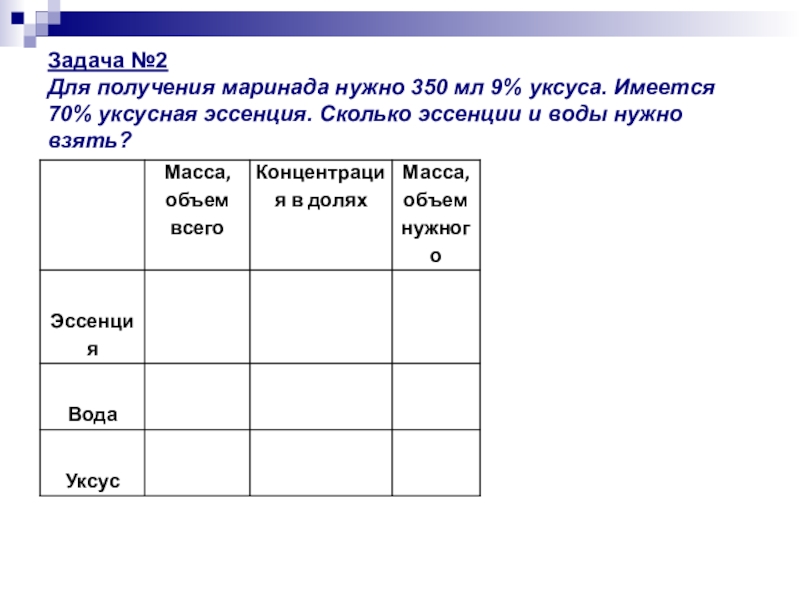
- 19. Задача №2 Для получения маринада нужно
- 20. Задача №2 Для получения маринада нужно
- 21. Задача №3 (Задание 11 № 99576) Имеется два
- 22. 0,3(2х+3)= 0,1х+ 0,4 (х+3), 0,6х+0,9=0,5х+1,2 , 6х+9=5х+12
- 23. Задача №4 Задание 11 № 99575 Имеется два сплава.
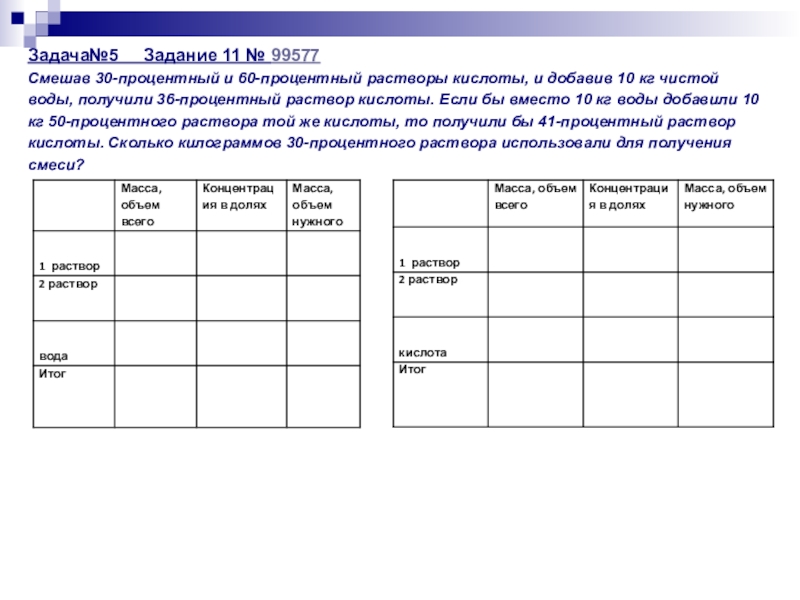
- 24. Задача№5 Задание 11 № 99577 Смешав 30-процентный
- 25. Задача№5 Задание 11 № 99577 Смешав 30-процентный
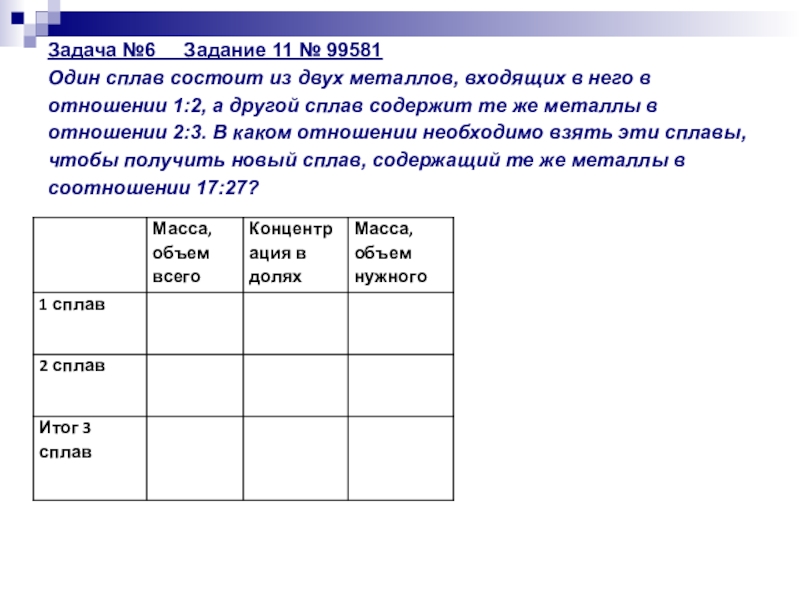
- 26. Задача №6 Задание 11 № 99581 Один
- 27. Задача №6 Задание 11 № 99581 Один
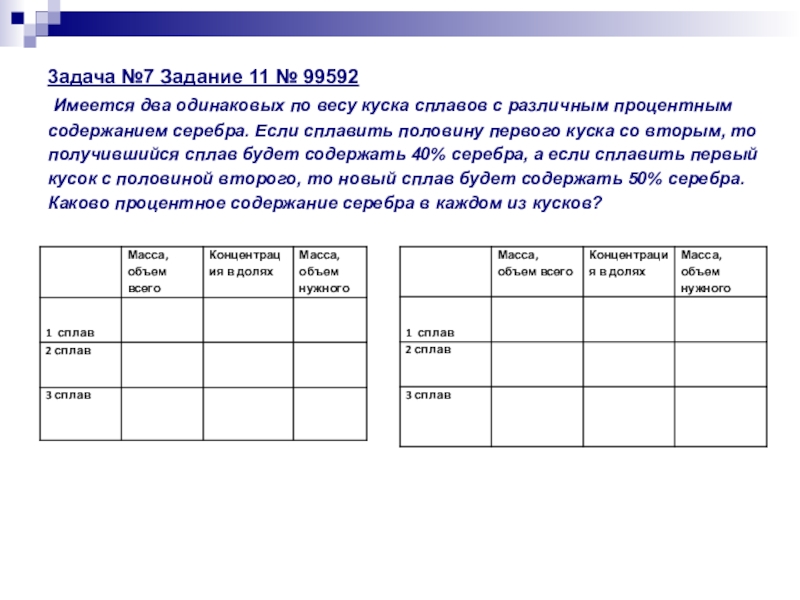
- 28. 3адача №7 Задание 11 № 99592 Имеется два
- 29. 3адача №7 Задание 11 № 99592 Имеется два
- 30. «Что может быть честнее и благороднее,Как научить
- 31. Спасибо за внимание!
Слайд 3
Цель:
профессиональное самосовершенствование участников мастер-класса
Задачи:
обобщить опыт работы по теме "Задачи на смеси и сплавы ";
прокомментировать эффективность применения табличного метода и метода креста при подготовке к ЕГЭ ;
создать условия для активного взаимодействия участников мастер - класса между собой.
Слайд 4
Чтобы лучше понимать условия задач, необходимо знать следующие понятия:
Все получающиеся
При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
Процент - одна сотая часть любого вещества.
Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.
Это отношение может быть выражено либо в дробях, либо в процентах.
Сумма концентраций всех компонент, составляющих смесь, равна единице.
Слайд 5типы задач
на вычисление концентрации;
на вычисление количества чистого вещества
на вычисление массы смеси (сплава).
Слайд 6Методы решения задач
алгебраический,
арифметический,
графический,
способ расчета по формуле,
при помощи
метод «креста» (конверт Пирсона),
метод «рыбки»,
метод «стаканчиков»,
при помощи прямоугольников.
Слайд 7«Правило креста» или «Конверт Пирсона».
Задача: «Имеется 30 кг 26% го раствора
26 10 значит 30 кг это 10 частей
40
50 14 а 14 частей – это 42 кг.
Ответ: 42 кг.
Слайд 8 Графический метод
Задача. В колбе было 200 г
ω1 ω2
0,8 Рассмотрев подобные треугольники, имеем
0,6
0,8 = 200
0,2 х , откуда х=50. .
0 50 200 Ответ: 50 г
Слайд 14 Метод стаканчиков
Задача. Сколько по массе 90%-го и
1 раствор 2 раствор смесь
Ответ:3,6 кг и 1,2 кг
Х
90
У
60
5,4
80
Слайд 15 При помощи универсальной таблицы Задача. Сколько нужно добавить воды
0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550
Ответ :1,55 кг воды.
Слайд 17
Слайд 18 Задача №1 Для получения напитка «Любовь» смешали 150г напитка «Грезы»
Слайд 19Задача №2 Для получения маринада нужно 350 мл 9% уксуса. Имеется
Слайд 20Задача №2 Для получения маринада нужно 350 мл 9% уксуса. Имеется
Слайд 21Задача №3 (Задание 11 № 99576) Имеется два сплава. Первый сплав содержит 10%
Слайд 220,3(2х+3)= 0,1х+ 0,4 (х+3), 0,6х+0,9=0,5х+1,2 ,
6х+9=5х+12 ,
х=3
2х+3=9
Ответ: 9 кг.
Задача
Слайд 23Задача №4 Задание 11 № 99575 Имеется два сплава. Первый содержит 10% никеля, второй
Слайд 24Задача№5 Задание 11 № 99577 Смешав 30-процентный и 60-процентный растворы кислоты, и
Слайд 25Задача№5 Задание 11 № 99577 Смешав 30-процентный и 60-процентный растворы кислоты, и
0,36(х+ y+10)= 0,3х+0,6y ,
0,41(х+ y+10)= 0,3х+0,6y+5 ;
х+ y+10=100,
30х+60 y =3600 ;
х+ y=90,
х+2 y=120;
y =30,
х=60.
Ответ: 60 кг
0,05(х+ y+10)= 5,
36(х+ y+10)= 30х+60 y;
Слайд 26Задача №6 Задание 11 № 99581 Один сплав состоит из двух металлов,
Слайд 27Задача №6 Задание 11 № 99581 Один сплав состоит из двух металлов,
Слайд 283адача №7 Задание 11 № 99592 Имеется два одинаковых по весу куска сплавов
Слайд 293адача №7 Задание 11 № 99592 Имеется два одинаковых по весу куска сплавов
Слайд 30«Что может быть честнее и благороднее,
Как научить тому, что сам наилучшим
Марк Фабий