Презентация, доклад на тему Логарифмы

Ленинградская

 

log3 x = 2;
log2 х = 5;
log4(x - 1) = 2 и т. д.
Решить логарифмическое уравнение — значит найти все его корни или доказать, что их нет.

а > О, а≠ 1 , называется показатель степени, в которую надо возвести а, чтобы получить b:
loga b = x <=> ах =b.
Из определения следует основное логарифмическое тождество: alogаb = b.
II. Свойства логарифмов.
При любом а > О, а ≠ 1, и любых положительных х и у верны следующие равенства:
loga(xy) = loga x + logaу
logа (х/у) = logаx - logау
logа(1/х)=- logа x
logс bª = аlogс b (для любого а ≠ 0);
logсª x= 1/а logсх (для любого а ≠ 0);
loga b = logсb / logса (формула перехода к новому основанию);
loga а = 1;
loga 1 = 0.

>0, а > 0, а ≠ 1, называется логарифмической.

2. Свойства.
Область определения — (0; +∞).
Область значений — множество действительных чисел.
При а > 1 функция монотонно возрастает, а при 0 < а < 1 — монотонно убывает (рис. 1).

1

1

х

у

х

у

(рис. 1).

а > 1

0 < а < 1

простой вид уравнений.
Решаются с помощью определения логарифма.
Разберем стандартные примеры.
Пример 1. log2(2x - 1) = 3.
По определению логарифма имеем:
23 = 2х — 1, 2х = 9, х = 4,5. Ответ:4,5.
Пример 2. logх+1 (2х2 + 1) = 2.
По определению логарифма имеем:
2х2 + 1 = (х + 1)2, х2 — 2х = 0, х(х - 2) = 0, х, = 0, х = 2.
При х = 0 основание логарифма х +1 = 1, поэтому х = 0 не является корнем уравнения. Ответ: 2.
Пример 3. log2 log3 log4(6x + 4) = 0.
По определению логарифма имеем:
log3 log4(6x + 4) = 1; log4(6x + 4) = = 3; 6х + 4= 64; 6х = 60; х = 10.
Ответ: 10.

(3)
2) log2(Зх2-8х+1) = 2; (3)
3) log5(х- 1) = 0; (2)
4) log3(x-12) = 2; (21)
5) log1/2(2-х) =-2. (-6)

к равенству, не содержащему их, называют потенцированием.
При решении уравнений loga f(х) = loga g(x) часто происходит расширение области определения уравнения за счет решения уравнения f (x) = g(x), а значит могут появиться посторонние корни. Поэтому, решив уравнение, следует проверить найденные корни подстановкой в данное уравнение.
Пример 1. log5 х2 = log5(6 — х).
Решение. Из равенства логарифмов чисел следует
х2 = 6 — х; х2 + х — 6 = 0; х1 = = -3; х2 = 2.
Проверка: 1. х1 = -3. log5 x2 = log5 9, log5(6 - х) = log5 9.
2. x2 = 2. log5 x2 = log5 4, log5(6 - x) = log5 4.
Ответ: -3; 2.

Из равенства логарифмов чисел следует: х2 - 4х- 5 = 7- Зх ; х2 – х- 12 =0; х1 = 4; х2= -3.
Проверка. 1) x1 =4 корнем данного уравнения быть не может, так как логарифмы отрицательных чисел не существуют.
2) х2 = -3. log3(x2 - 4х - 5) = log3(9 +12 -5) = log3 16, log3(7 - Зх) = log3 16.
Ответ:-3.
Пример 3. log3(x + 2) + log3(x + 1) = log3(x + 5).
Потенцируя данное равенство, получим:
log3(x + 2)(x + 1) = log3(x + 5),
(х+ 2)(х+ 1) = х+ 5; х2 + 2х — 3 = 0; х, = —3; х2 = 1.
Проверка. 1) x1 = - 3. Число -3 корнем данного уравнения не является, так как логарифмы отрицательных чисел не существуют.
2) х2 = 1. log3 3 + log3 2 =log3 6, log3 6= log3 6.
Ответ: 1.

= log0.5(2x-5); 2

2)lg(2x+3) = 2lgx; 3

3)0,51g(2x-l)=l-lgx9. 13

31og2х = 4.
Обозначим log2 х через у.
Данное уравнение примет вид: у2 - Зу - 4 = 0; у1, = 4; у2 = -1.
log2 х = 4; х = 16. log2 x = -1;х = ½.
Проверка. х = 16; 4= 4, х2 = 2 , 4= 4.
Ответ:1/2, 16.

Решите самостоятельно: Ответы:
1) log52x - 3 log5x =4. , 5 4 ; 1/5.

2) log224x + log2 (2х /8) =8. 1/64; 2.

основанию.

loga b = logсb / logса (формула перехода к новому основанию)
loga b = 1/ log ba
Пример 1.
21og5 х + 21ogx 5 = 5, 21og5 х+2 *1/1og5x =5
Обозначим log5 x = v.
2у2-5у+2 = 0; у1 = 2, y2=1/2.
log5x = 2; x1 = 25. log5x= ½; x2= √5 .
Проверка. 1). x1 = 25, 21og5 25 + 21og25 5 = 4+1 = 5.
2). X2= √5 , 21og5 √5 + 21og √5 5 = 1 + 4 = 5.
Ответ: 25, √5.
Решите самостоятельно: Ответы
log4 x + log16 x + log2 x = 7; 16
log3 x + log1/9 x + log1/3 x = 6. 1/27

х1оġ2х + 2 = 8.
Решение. Логарифмируя обе части уравнения (х > 0),
получим log2 х1оġ2х + 2 = log2 8;
(log2 x + 2) log2 x = log2 8; log22 х + 21og2 x - 3 = 0;
log2 x = y; y2 +2у - 3 = 0; y = -3, у=1.
log2 x = -3, x1 = 1/8; log2 x = 1, X2 = 2.
Проверка.
1) x1 = 1/8, (1/8)log21/8 + 2 = 8, (2-3) log21/8 + 2 = 8, 8=8. .
2) x2 = 2, 2log22 + 2 = 23 = 8.
Ответ:1/8; 2.
Решите самостоятельно:
1. х1ġх =100х.

(х), где f(x) и р (х) — функции.
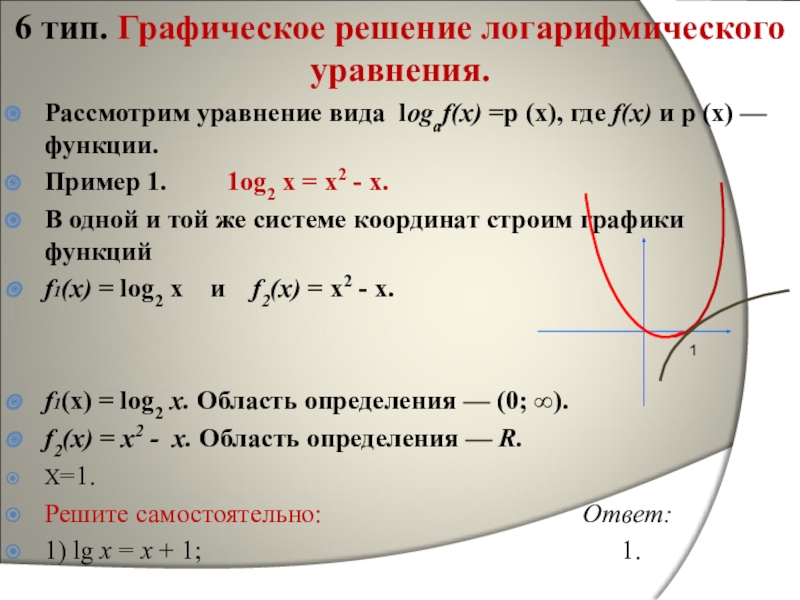
Пример 1. 1og2 х = х2 - х.
В одной и той же системе координат строим графики функций
f1(x) = log2 х и f2(x) = х2 - х.


f1(х) = log2 x. Область определения — (0; ∞).
f2(x) = х2 - х. Область определения — R.
Х=1.
Решите самостоятельно: Ответ:
1) lg х = х + 1; 1.

1