- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Квадратное уравнение
Содержание
- 1. Квадратное уравнение
- 2. Цель урока:Обобщить,
- 3. Решите уравнения (устно):1. x²=0
- 4. Впервые квадратные уравнения сумели решить математики древнего
- 5. Франсуа Виет (1540-1603) — французский математик. Разработал
- 6. Кроссворд.1.Третья степень числа. 2.Подкоренное выражение в формуле
- 7. Алгоритм решения биквадратного уравнения. Метод решения -
- 8. х2у2 – 5у – 36 = 025
- 9. 3 шагВернуться к первоначальной переменной х, подставив
- 10. 7х2+2х(у–3) (у+5)=16х2+3х+1у2+4у – 6 = –13х–5у2 –
- 11. Решите уравнение
- 12. Физкультминутка!
- 13. Возвратные (симметричные) уравнения 4-ой степени
- 14. Домашнее задание.Выбрать различные прототипы квадратных уравнений.
Слайд 1МОУ лицей г.Фрязино
8 класс
учитель Бурова Марина Васильевна
2016г.
Решение уравнений, приводимых к квадратным.
Слайд 2 Цель урока:
Обобщить, систематизировать и углубить учебный
Развивать внимание, память, речь, логическое мышление, самостоятельность.
Воспитать стремление достигнуть поставленную цель, чувство ответственности, уверенности в себе, умение работать в коллективе.
Слайд 3 Решите уравнения (устно):
1. x²=0
2. 4x²-16=0
3. 3x²+12=0
4. 7x²-3x=0
5. -x²+7=0
6. x²+6x-7=0
7. x²-9x-10=0
Я) нет решений
Н) x1=1 x2=-7
О) x1=-1 x2=10
Ф) x=0
И) x1,2=±√7
З) x1=0 x2=3/7
Р) x=±2
Ответы:
Слайд 4Впервые квадратные уравнения сумели решить математики древнего Египта. Вавилоняне умели решать
Общее правило решения квадратных уравнений, преобразованных в вид
х2 + bх = с, было описано немецким математиком М. Штифелем. Он и сформулировал в 1544 году общее правило решения квадратных уравнений, приведенных к единому каноническому виду
х2 + bх + с = 0 при всевозможных вариациях знаков и коэффициентов b и с
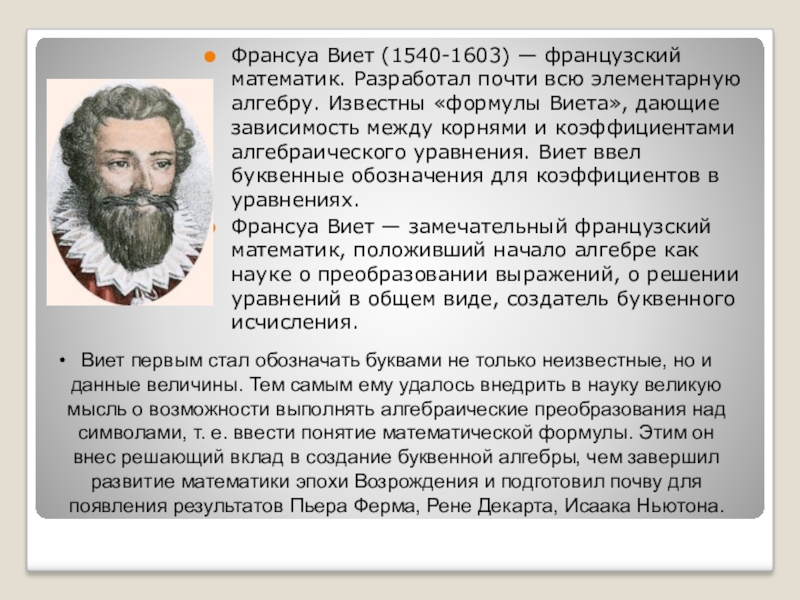
Слайд 5Франсуа Виет (1540-1603) — французский математик. Разработал почти всю элементарную алгебру.
Франсуа Виет — замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления.
Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т. е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Пьера Ферма, Рене Декарта, Исаака Ньютона.
Слайд 6Кроссворд.
1.Третья степень числа.
2.Подкоренное выражение в формуле корней квадратного уравнения.
3.Значение
4.Уравнения, имеющие одинаковые корни.
5.Равенство с переменной.
6.Квадратное уравнение, с первым коэффициентом равной единице.
7.Многочлен в левой части квадратного уравнения.
8.Равенство, содержащее числа и переменные.
9.Французский математик.
10.Числовой множитель - в произведении.
11.Один из видов квадратного уравнения.
12.Множество корней уравнения.
Б и к в а д р а т н о е
Слайд 7Алгоритм решения биквадратного уравнения. Метод решения - замена переменной. ах4 + bх2
1. Ввести замену переменной: пусть х² = t,
тогда (х²)²=t²
2. Составить квадратное уравнение с новой переменной:
аt² + bt + с = 0 (2)
3. Решить новое квадратное уравнение (2).
4.Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного уравнения.
7. Записать ответ.
Слайд 8х2
у2 – 5у – 36 = 0
25 + 4·36 = 169,
х2 = 9
х2 = - 4
у1 = 9, у2 = – 4
Корней нет
х1 = 3
х2 = – 3
3; – 3
МЕТОД ВВЕДЕНИЯ НОВОЙ ПЕРЕМЕННОЙ
Слайд 93 шаг
Вернуться к первоначальной переменной х, подставив найденные значения вместо введенной
х2+3х = –10 или х2+3х = 4
х2+3х+10=0
D=9-4·10=-31
D < 0,
Корней нет
х2+3х – 4=0
х1=1;
х2 = – 4.
Ответ: – 4, 1.
Пусть у = х2+3х, тогда
(у+2)(у+4) = 48
Ввести новую переменную у, которой обозначить по-вторяющееся выражение х2+3х. Записать получив-шееся уравнение
Решить уравнение относительно новой переменой
1 шаг
2 шаг
у2 + 4у + 2у + 8 – 48 = 0
у2 + 6у – 40 = 0
у1 = – 10 , у2 = 4.
Слайд 107х2+2х
(у–3) (у+5)=16
х2+3х+1
у2+4у – 6 = –1
3х–5
у2 – 4у = 12
3х2+5х
(у+2)(у–5) –5=16
х2
х2
у2
16у2 – 8у + 1 = 0
Слайд 11Решите уравнение
(x²+6x) ² +
Решение.
(x²+6x) ² + 2 (Х² +6х + 9) -81 =0
Пусть x²+6x = t, тогда
t ² +2 (t +9)-81=0,
t ² +2 t -63=0,
t=-9 или t=7.
Получили:
x²+6x=-9 или x²+6x=7
x²+6x+9 =0 x²+6x-7=0
x=-3 х1=-7, х2=1
Ответ: - 7; -3; 1.
Слайд 13Возвратные (симметричные) уравнения 4-ой степени Возвратными (симметричными) уравнениями 4-ой степени называют
ax4 + bx3 + cx2 + bx + a = 0,
а также уравнения вида
ax4 + bx3 + cx2 – bx + a = 0,
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение, разделим его на x2. В результате получится уравнение