- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Квадратичная функция. Материалы к уроку
Содержание
- 1. Квадратичная функция. Материалы к уроку
- 2. ОпределениеКвадратичной функцией называется функция, которую можно задать
- 3. Построение графика функции у = 2х²Построим
- 4. Построение графика функции у =
- 5. Наложение графика функции у =
- 6. Построение графика функции у=-1/2х² Построим график
- 7. Наложение двух графиков функций у = 1/2х²
- 8. Свойства функции у=ах² при а>0Если х=0, то
- 9. Свойства функции у = ах² при а
- 10. Задания для решения №1Постройте график функции у=¼х².
- 11. Движение графика по оси уГрафик функции у=1/2х²+3
- 12. Движение графика по оси хГрафик у=1/2(х-5)² -
- 13. Перемещение графика функции по оси х и
- 14. Задания для решения №2Изобразите схематически график каждой
- 15. Алгоритм построения графика квадратичной функции1) График –
- 16. Построение графика функции
- 17. Построение графика функции у =
- 18. Построение графика функции
- 19. Задания для решения №3Квадратичная функция задана формулой:
- 20. Показ окончен, спасибо за внимание!
Слайд 2Определение
Квадратичной функцией называется функция, которую можно задать формулой вида y=ax² +bx+c,
Парабола – график функции квадратного трехчлена. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 – максимум. Точки пересечения (если они есть) с осью абсцисс – корни соответствующего квадратного уравнения ах² + bх + с = 0
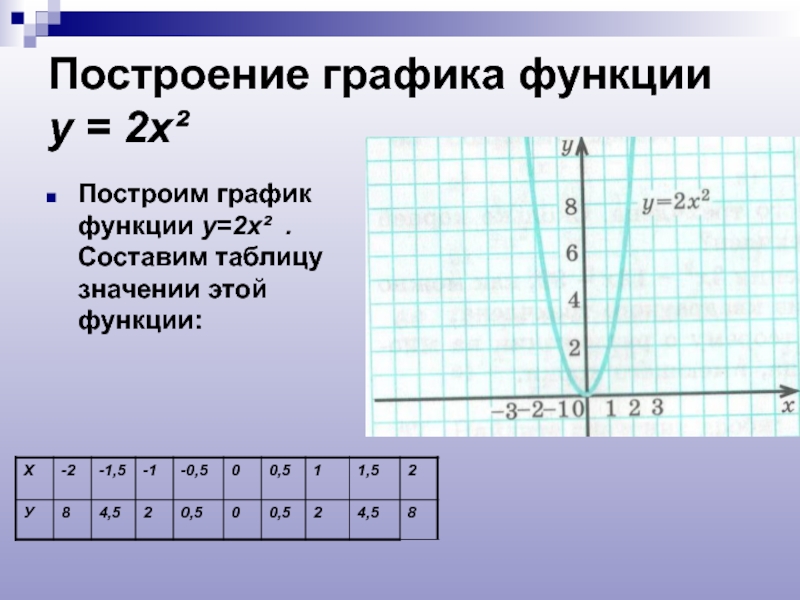
Слайд 3Построение графика функции
у = 2х²
Построим график функции у=2х² . Составим
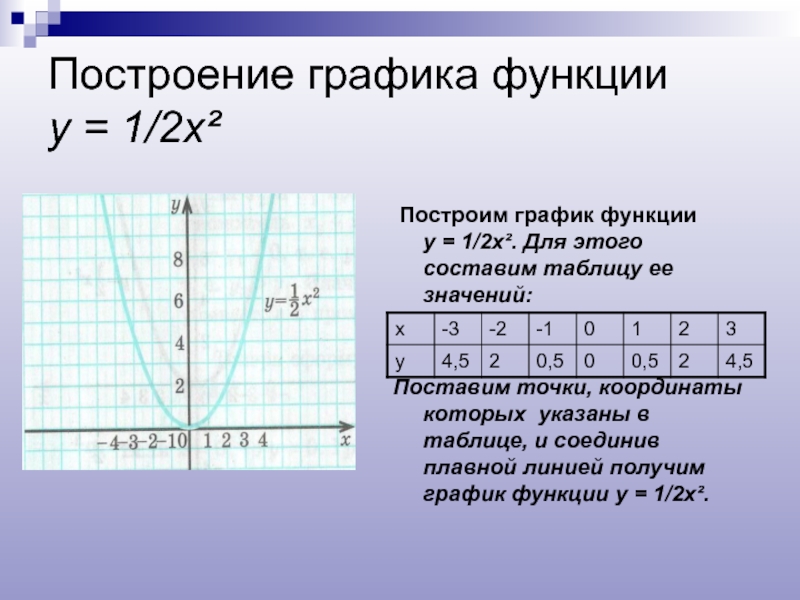
Слайд 4Построение графика функции у = 1/2х²
Построим график функции
Поставим точки, координаты которых указаны в таблице, и соединив плавной линией получим график функции у = 1/2х².
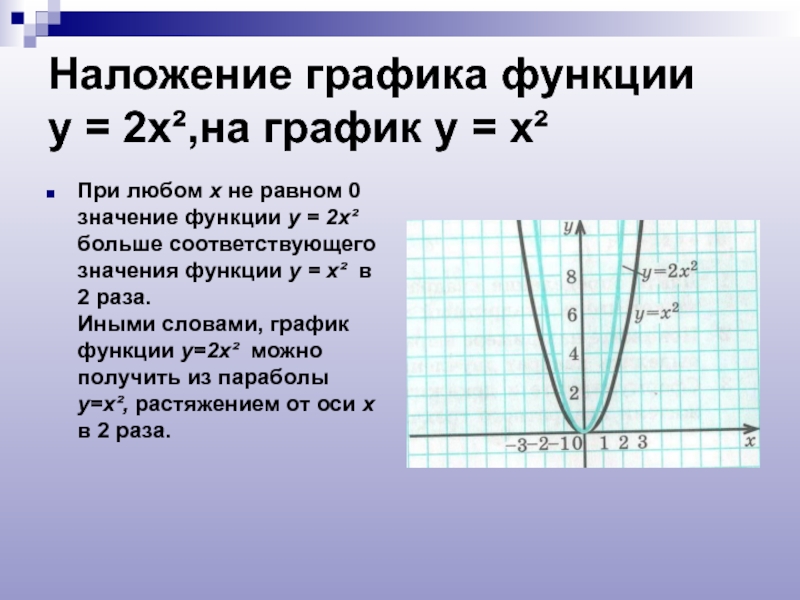
Слайд 5Наложение графика функции у = 2х²,на график у =
При любом х не равном 0 значение функции у = 2х² больше соответствующего значения функции у = х² в 2 раза. Иными словами, график функции у=2х² можно получить из параболы у=х², растяжением от оси х в 2 раза.
Слайд 6Построение графика функции у=-1/2х²
Построим график функции у = -1/2х²,
Воспользовавшись этой таблицей, построим график функции
у=-1/2х²
Слайд 7Наложение двух графиков функций у = 1/2х² с противоположными знаками
При любом
Слайд 8Свойства функции у=ах² при а>0
Если х=0, то у=0. График функции проходит
Если х≠0, то у>0. График функции расположен в верхней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0; +∞).
Наименьшее значение, равное нулю, функция принимает при х=0, наибольшего значения не имеет. Областью значений функции является промежуток [0; +∞)
Слайд 9Свойства функции у = ах² при а < 0
Если х=0, то
Если х≠0, то у<0. График функции расположен в нижней полуплоскости.
Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
Функция возрастает в промежутке (-∞; 0] и убывает в промежутке [0; +∞).
Наибольшее значение, равное нулю, функция принимает при х=0, наименьшего значения функция не имеет. Областью значений функции является промежуток (-∞; 0].
Слайд 10Задания для решения №1
Постройте график функции у=¼х². Найдите: а) значение у
Постройте график функции у=-2х² и найдите: а)значение у=-1,5; 0,6; 1,5; б) значение х, при которых у = -1; -3; -4,5; в) промежуток убывания функции.
Постройте в одной системе координат графики функций у=0,4х² и у=-0,4х². Какова область значений каждой функции?
Найдите координаты точек пересечения графиков функций у=-х² и у=2х-3. Выполните графическую иллюстрацию
Принадлежит ли графику функции у=-100х² точка: а) М(1,5; -225); б) К(-3; - 900); в) Р(2; 400)?
ПРОВЕРЬ СЕБЯ
Слайд 11Движение графика по оси у
График функции у=1/2х²+3 – парабола, полученная в
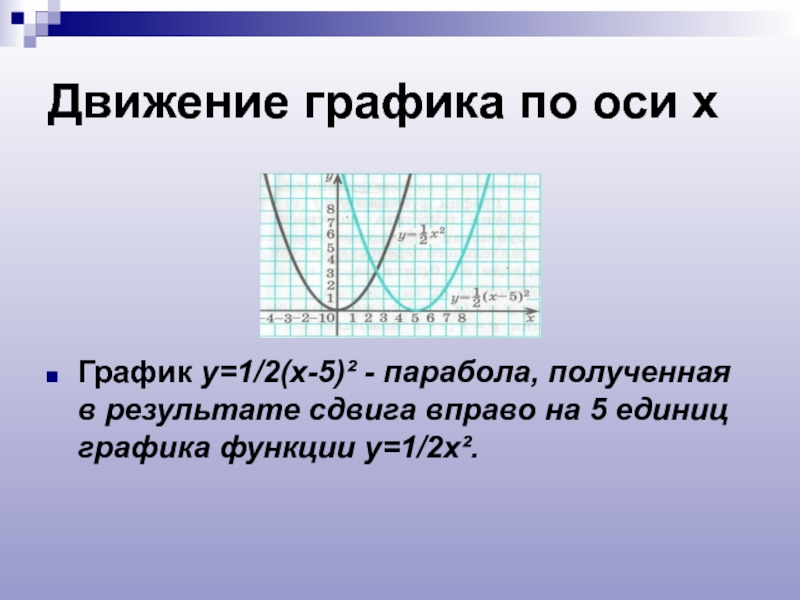
Слайд 12Движение графика по оси х
График у=1/2(х-5)² - парабола, полученная в результате
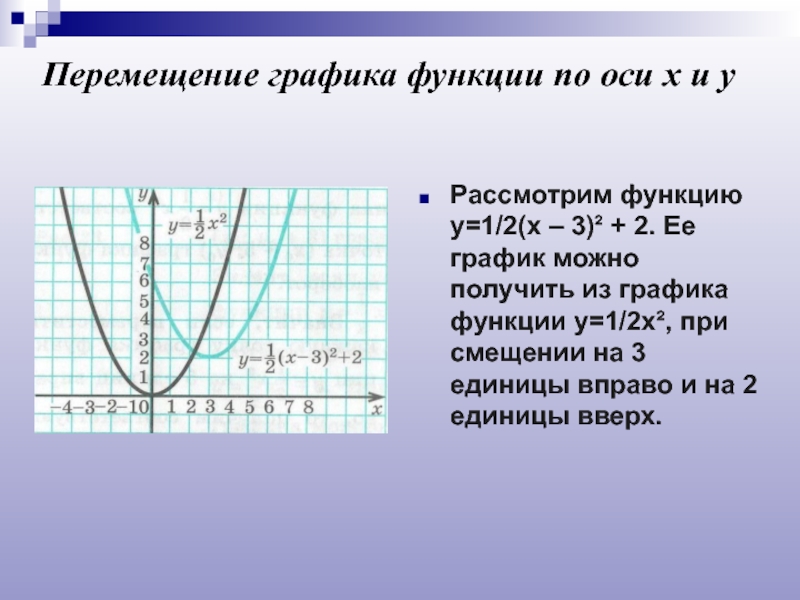
Слайд 13Перемещение графика функции по оси х и у
Рассмотрим функцию у=1/2(х –
Слайд 14Задания для решения №2
Изобразите схематически график каждой функции (отметьте вершину параболы
С помощью шаблона параболы у=х² постройте график функции: а) у=х²-4; б) у=-х²+3; в) у=(х-5)²; г) у=(х+3)².
Используя шаблон параболы у=х², постройте график функции: а) у=х²+2; б) у=-х²-1; в) у=(х+4)²; г) у=-(х-3)².
Изобразите схематически график функции: а) у=1/4(х-2)²-3; б) у=-1/4(х-3)².
С помощью шаблона параболы у=х² постройте график функции: а) у=(х+3)²-4; б) у=-(х+4)²-2.
ПРОВЕРЬ СЕБЯ
Слайд 15Алгоритм построения графика квадратичной функции
1) График – парабола, ветви направлены в
2) У = 0, если (решить квадратное уравнение)
3) КВП: m = -в/2а
n = -D/4a
4) Если х = 0, то у = (просчитать чему будет равен у).
Пример:
У = 0,5х² + 3х + 0,5
График – парабола, ветви направлены вверх (а > 0)
у = 0, если 0,5х² + 3х + 0,5 =0
х · х = 1 х ≈ - 5,8
х + х = -6 х ≈ - 0,2
3) КВП: m = - 3/ 1= -3; n = (9 – 4 · 0,5 · 0,5)/(4 · 0,5) = - 4
4) Если х = 0, то у = 0,5.
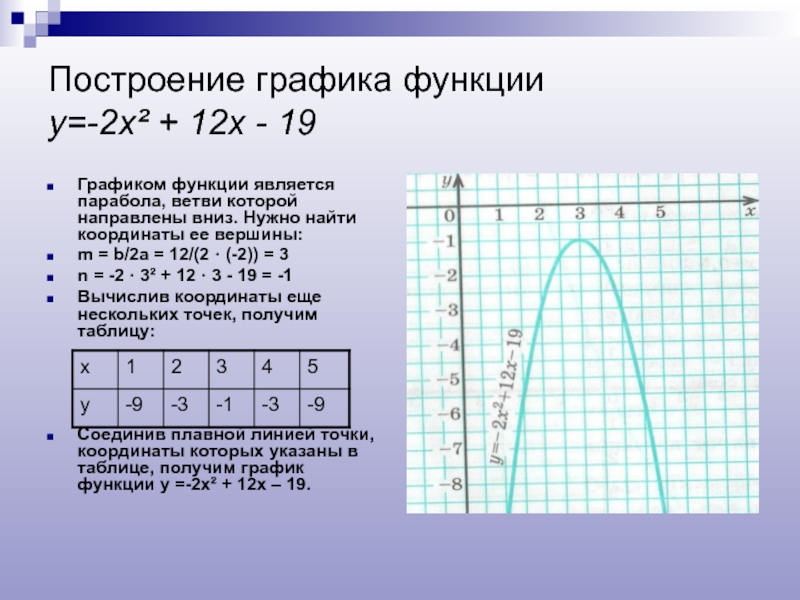
Слайд 16Построение графика функции у=-2х²
Графиком функции является парабола, ветви которой направлены вниз. Нужно найти координаты ее вершины:
m = b/2а = 12/(2 · (-2)) = 3
n = -2 · 3² + 12 · 3 - 19 = -1
Вычислив координаты еще нескольких точек, получим таблицу:
Соединив плавной линией точки, координаты которых указаны в таблице, получим график функции у =-2х² + 12х – 19.
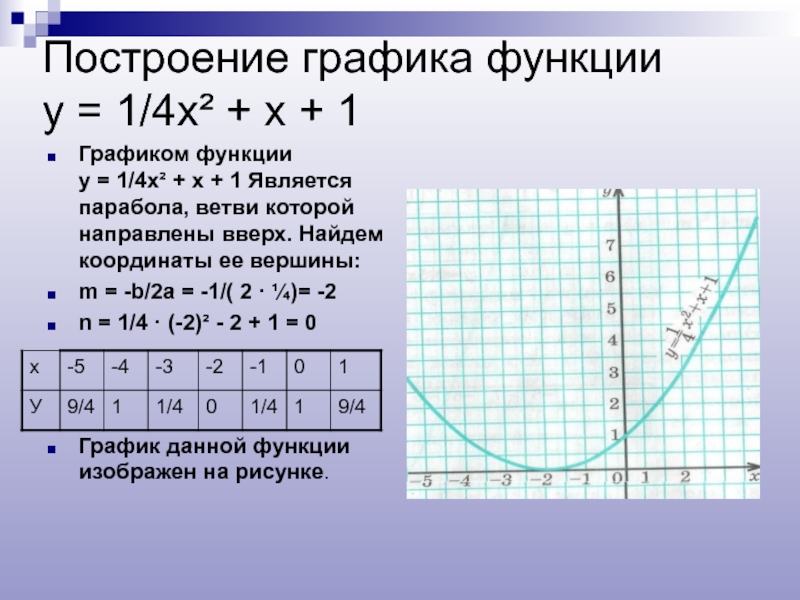
Слайд 17Построение графика функции у = 1/4х² + х +
Графиком функции у = 1/4х² + х + 1 Является парабола, ветви которой направлены вверх. Найдем координаты ее вершины:
m = -b/2а = -1/( 2 · ¼)= -2
n = 1/4 · (-2)² - 2 + 1 = 0
График данной функции изображен на рисунке.
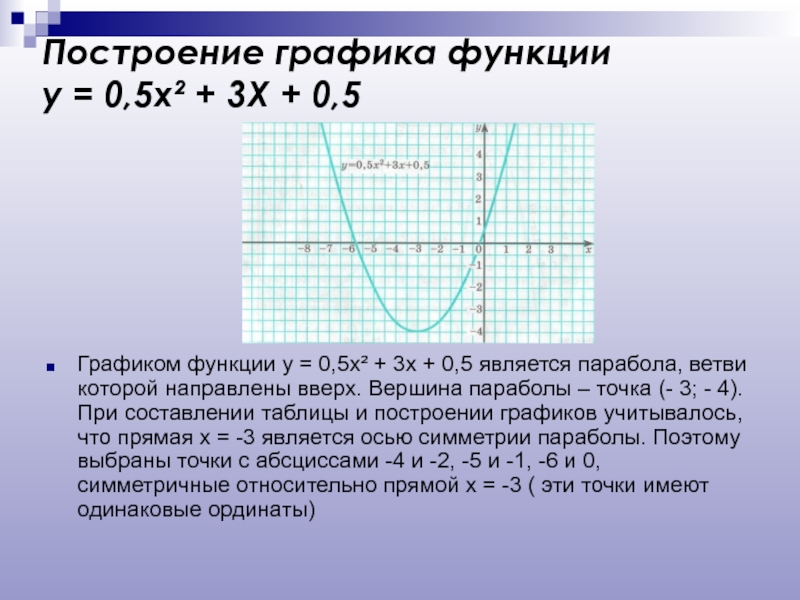
Слайд 18Построение графика функции
Графиком функции у = 0,5х² + 3х + 0,5 является парабола, ветви которой направлены вверх. Вершина параболы – точка (- 3; - 4). При составлении таблицы и построении графиков учитывалось, что прямая х = -3 является осью симметрии параболы. Поэтому выбраны точки с абсциссами -4 и -2, -5 и -1, -6 и 0, симметричные относительно прямой х = -3 ( эти точки имеют одинаковые ординаты)
Слайд 19Задания для решения №3
Квадратичная функция задана формулой: а) у=х²-4х+7;
Постройте график функции у=2х²+8х+2 и найдите, используя график: а) значение у при х=-2,3; -0,5; 1,2; б) значение х, при которых у=-4; -1; 1,7; в) нули функции, промежутки, в которых у>0, у<0; г) промежутки возрастания и убывания функции, наименьшее значение функции.
Постройте график функции у=-х²+2х+8 и найдите используя график: а) значение функции при х=2,5; -0,5; -3; б) значения аргумента, при котором у=6; 0; -2; в) нули функции, промежутки в которых у>0, у<0; г) промежутки возрастания и убывания функции, область значений функции.
Постройте график функции: а) у=0,5х²-2; б) у=х²-4х+4; в) у=-х²+2х.
Постройте график функции: а) у=(х-2)(х+4); б) у=-х(х+5)
ПРОВЕРЬ СЕБЯ
>0, у<0