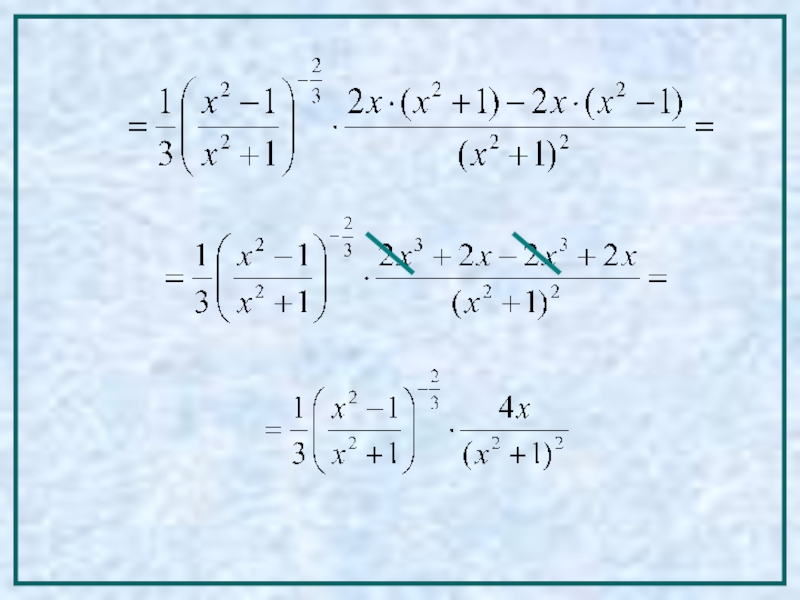- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Күрделі функцияның туындысы 10 сынып
Содержание
- 1. Күрделі функцияның туындысы 10 сынып
- 2. Анықтама Айнымалы y - u, y=f(u) айнымалының
- 3. ТЕОРЕМА Егер y=f(u), u=φ(x) – өз аргументтерінің
- 4. Дәлел: Х аргументіне нөлге тең емес Δх
- 5. Шексіз аз шаманың функция шектерімен
- 6. u=φ(x) функция шарты бойынша дифференцияланғандықтан,
- 7. Күрделі функцияны дифференциялау ережесін басқаша жазуға болады:немесе
- 8. Мысалдар. 1Күрделі функцияның туындыларын табу:
- 9. Шешім:
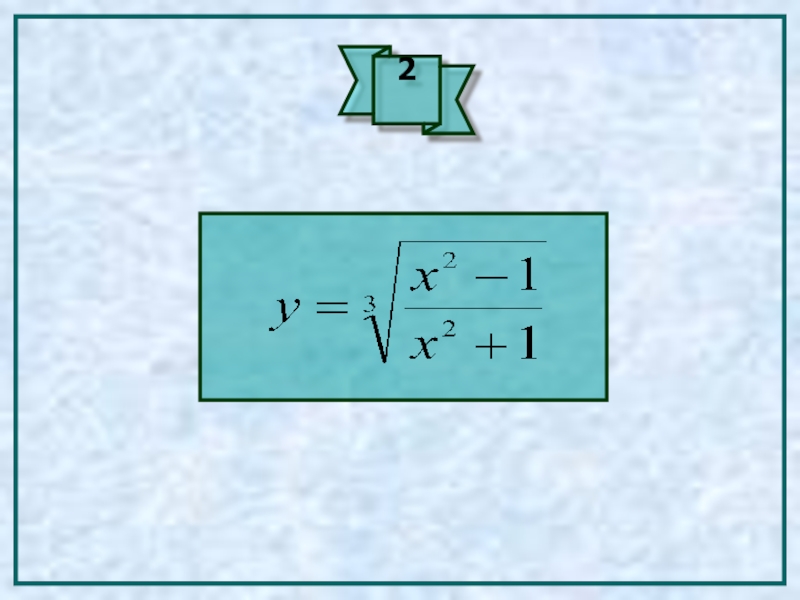
- 10. 2
- 11. Шешім:
- 12. Слайд 12
Анықтама Айнымалы y - u, y=f(u) айнымалының функциясы болсын.Және айнымалы u - x, u=φ(x) айнымалының функциясы болсын.Яғни күрделі функция берілген:
Слайд 2Анықтама
Айнымалы y - u, y=f(u) айнымалының функциясы болсын.
Және айнымалы u
- x, u=φ(x) айнымалының функциясы болсын.
Яғни күрделі функция берілген:
Слайд 3
ТЕОРЕМА
Егер y=f(u), u=φ(x) – өз аргументтерінің дифференцияланған функциялары болса, онда
күрделі функцияның туындысы бар және тәуелсіз айнымалы бойынша аралық аргументтің өз туындысының көбейтілген аралық аргумент бойынша аталмыш функция туындысына тең:
Слайд 4Дәлел:
Х аргументіне нөлге тең емес Δх өсімін берейік, онда u=φ(x),
y=f(u) функциялары Δu и Δy өсімдерін алады.
Δu нөлге тең емес деп болжайық, онда y=f(u) функцияның дифференцияланатын күшіне қарай мынаны аламыз:
өлшемі Δu бағынышты емес.
Слайд 5 Шексіз аз шаманың функция шектерімен байланысы туралы теорема негізінде
шек белгісінде тұрған функцияны осы шектің қосындысы және шексіз аз шама қосындысы ретінде елестетуге болады:
Бұдан:
мұнда α(Δu) – шексіз аз шама, онда
Теңдіктің екі бөлігін Δx-ке бөлеміз:
Слайд 6 u=φ(x) функция шарты бойынша дифференцияланғандықтан, ол x нүктесінде үздіксіз.
Бұдан
мынау шығады:
және
Соңғы теңдікте мына шекке көшеміз