- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конверт Пирсона. Презентация по математике по теме Задачи на проценты
Содержание
- 1. Конверт Пирсона. Презентация по математике по теме Задачи на проценты
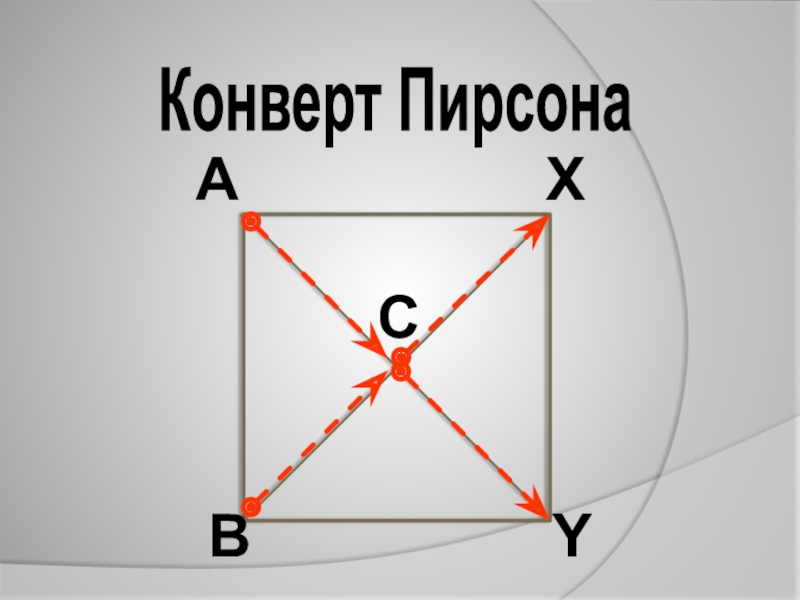
- 2. ABCXYКонверт Пирсона
- 3. Карл ПирсонКарл Пирсон родился 27 марта 1857
- 4. Задачи решаемые при помощи конверта При
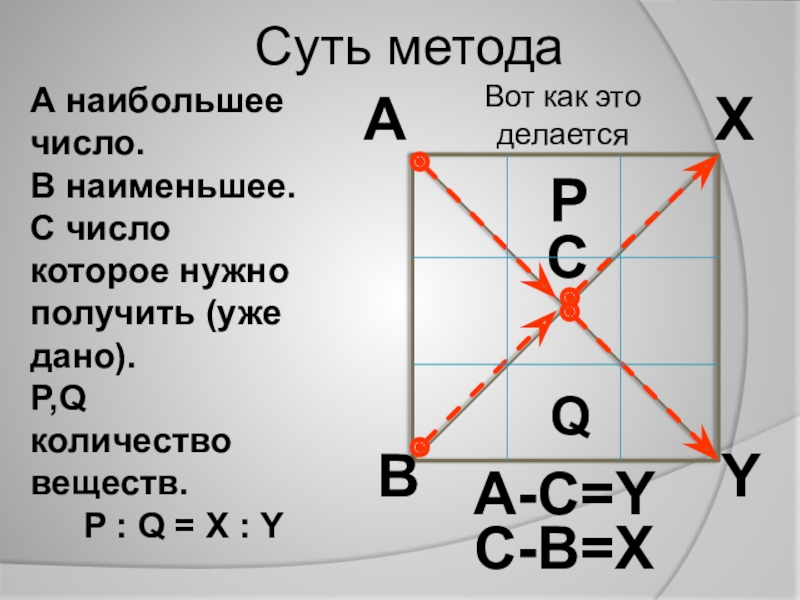
- 5. C-B=XA-C=YABCXYQА наибольшее число.В наименьшее.С число которое нужнополучить
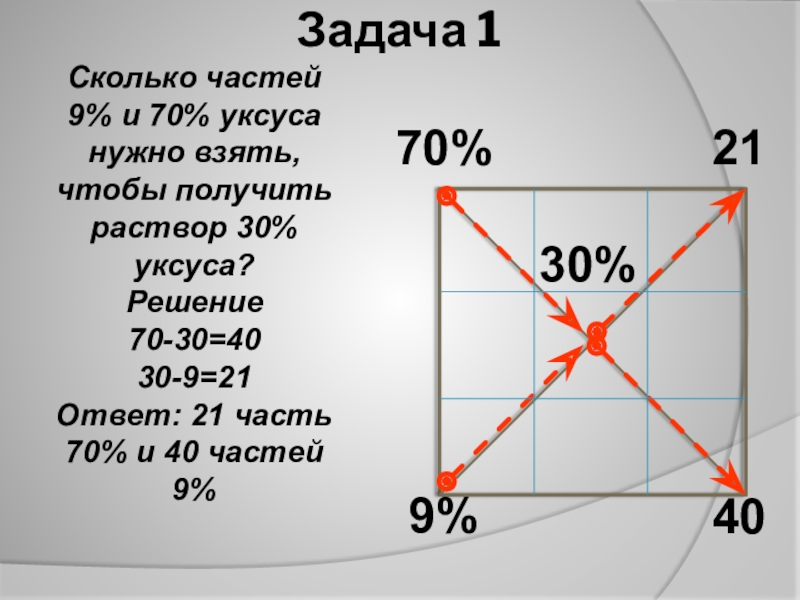
- 6. Задача 170%9%30%2140Сколько частей 9% и 70%
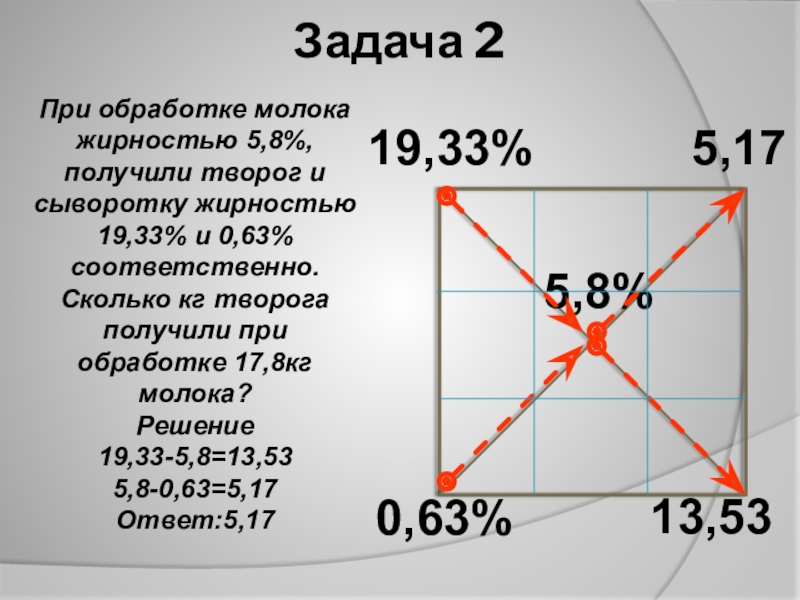
- 7. Задача 219,33%0,63%5,8%5,1713,53При обработке молока жирностью 5,8%,
- 8. Стандартное решениеПусть Хг - масса творогаYг –
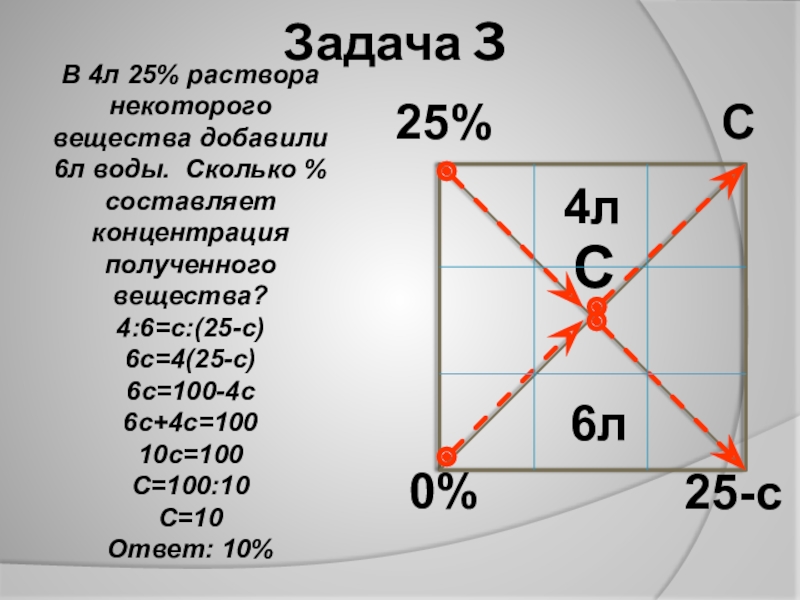
- 9. Задача 325%0%CС25-сВ 4л 25% раствора некоторого вещества
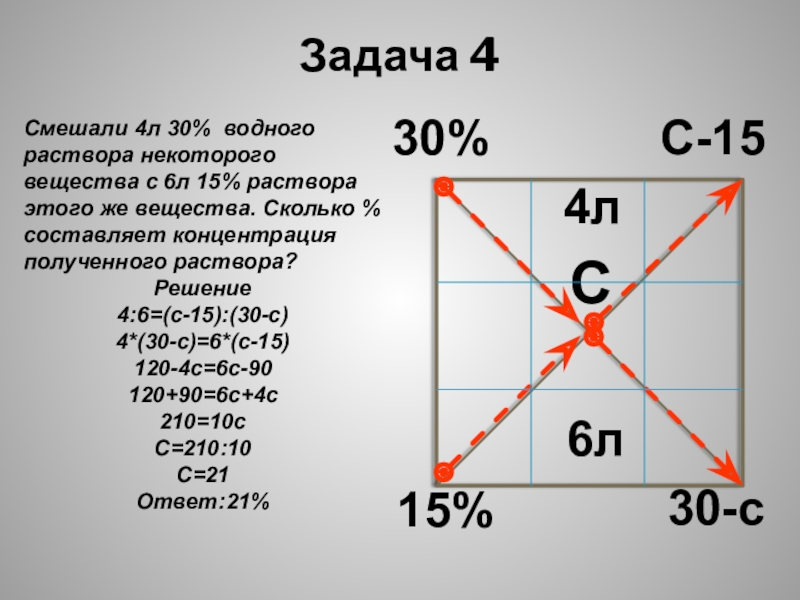
- 10. Задача 430%15%CС-1530-с4л6лСмешали 4л 30% водного раствора некоторого
- 11. Задача 540%5%25%2015175-ххИмеется два сплава. Первый содержит 5%
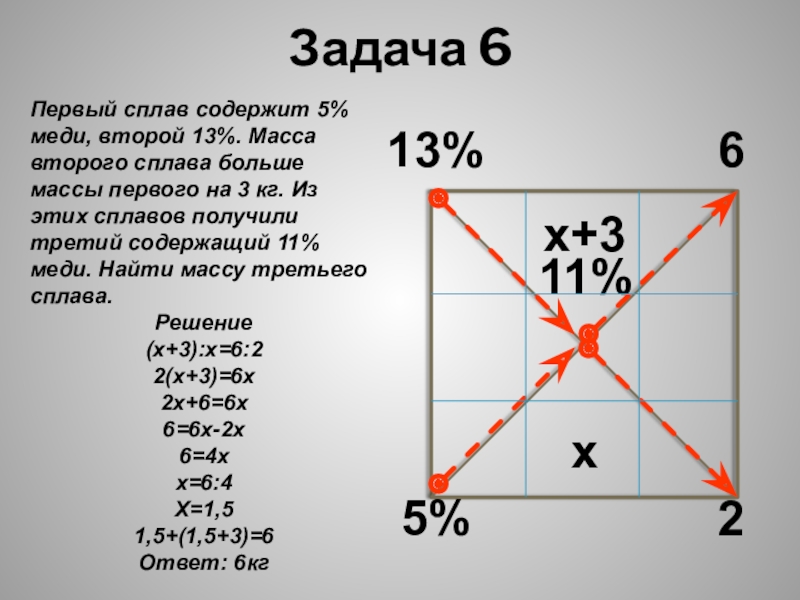
- 12. Задача 613%5%11%62Первый сплав содержит 5% меди, второй
- 13. Стандартное решение этой задачиI сплавX кг –
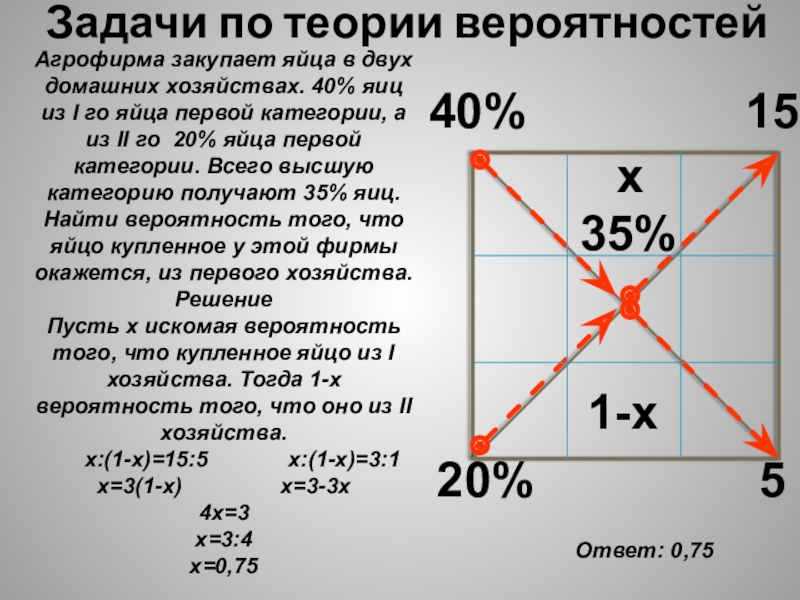
- 14. Задачи по теории вероятностей40%20%35%155Ответ: 0,75Агрофирма закупает яйца
- 15. Задача 7100 : 20=(72-Y) : (X-72)5= (72-Y)
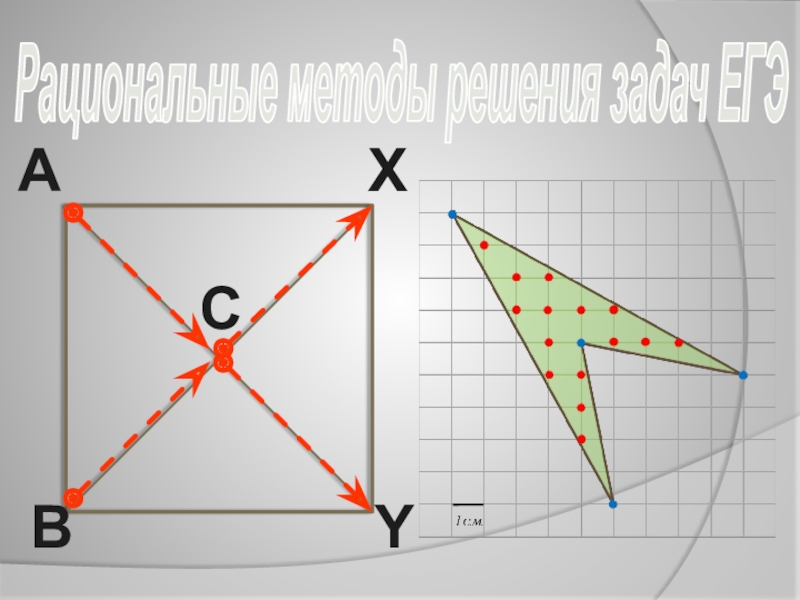
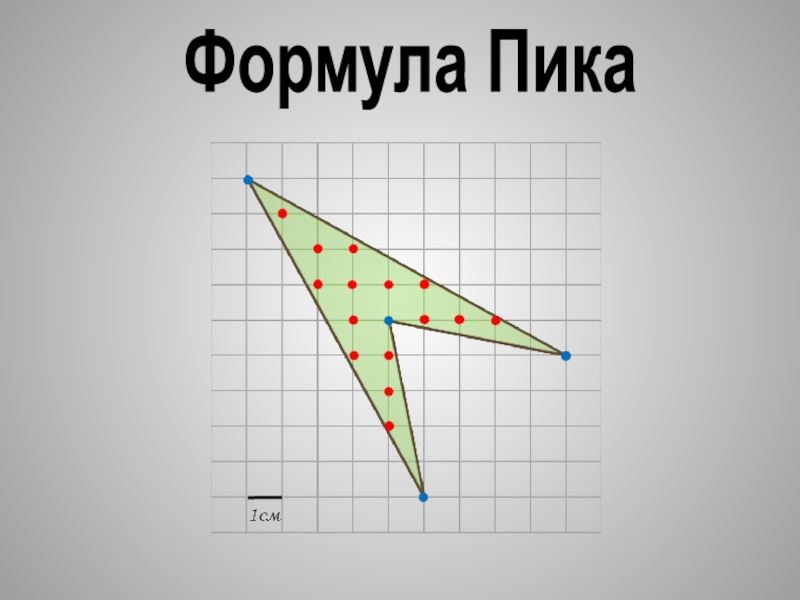
- 16. Формула Пика
- 17. Георг Пик Австрийский математик Георг Александр Пик родился
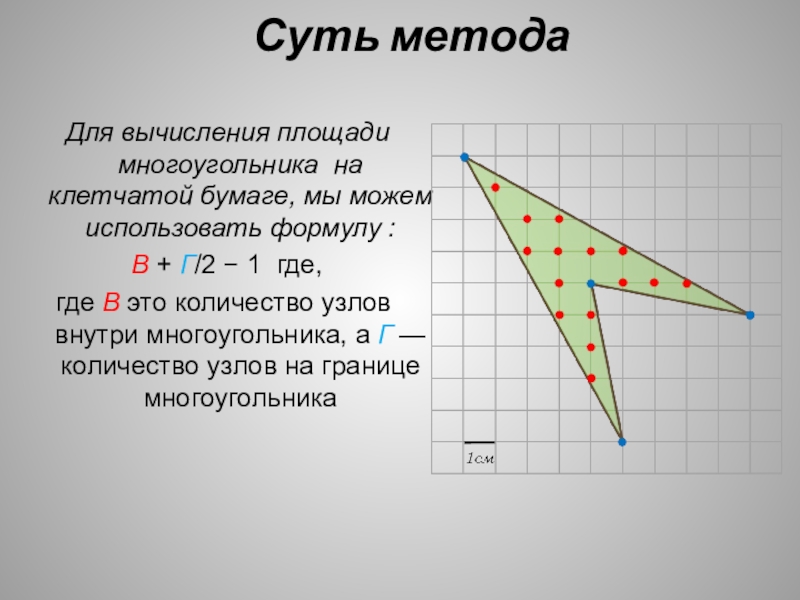
- 18. Суть метода Для вычисления площади
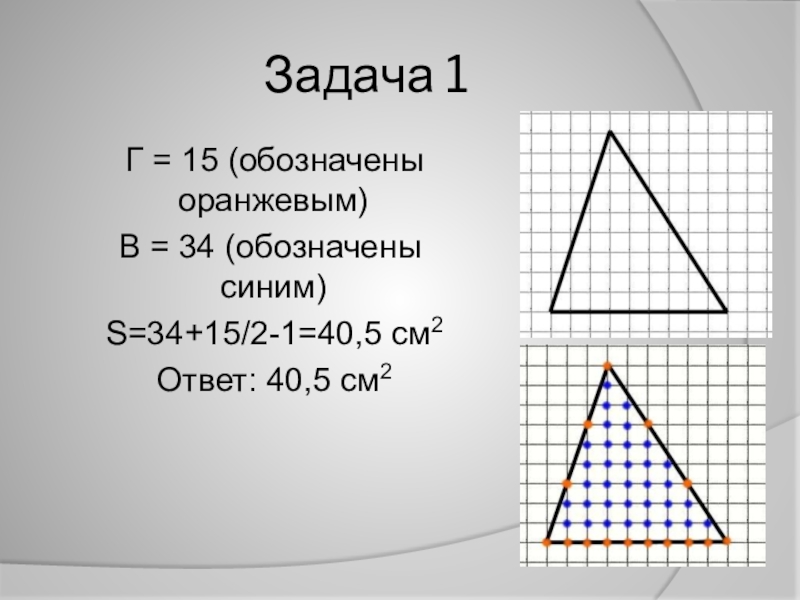
- 19. Задача 1 Г = 15 (обозначены
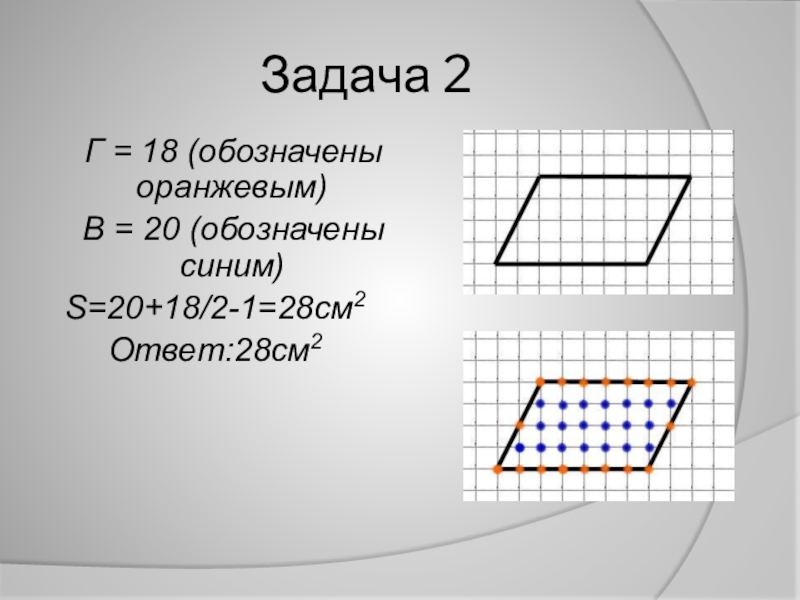
- 20. Задача 2 Г = 18 (обозначены оранжевым) В = 20 (обозначены синим)S=20+18/2-1=28см2Ответ:28см2
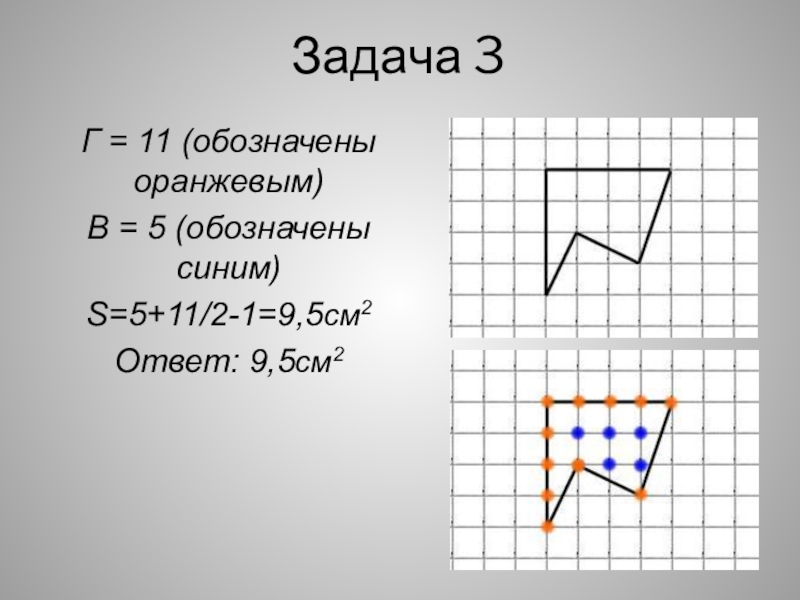
- 21. Задача 3Г = 11 (обозначены оранжевым)В = 5 (обозначены синим)S=5+11/2-1=9,5см2Ответ: 9,5см2
- 22. Задача 4Г = 7 (обозначены жёлтым)В = 2(обозначены синим)S=2+7/2-1=4,5см2Ответ: 4,5см2
- 23. Задача 5Г = 4 (обозначены жёлтым)В =0S=0+4/2-1=1см2Ответ: 1см2
- 24. Метод рационализации при решении уравнений с модулями
- 25. Уравнение 1│2x-1│= │x-1│(2x-1-x+1)(2x-1+x-1) = 0x(3x-2) = 0x = 0 x = Ответ: 0;
- 26. Уравнение 2 │x+1│= 2x-1
- 27. Уравнение 3│ x2+3x│= 2(x+1)│ x2+3x│- 2(x+1) =
- 28. ЗаключениеПродемонстрированные методы решения задач не являются чрезвычайно
- 29. Литература1. Я. И. Перельман «Занимательная математика»; издательство
- 30. СПАСИБО ЗА ВНИМАНИЕ
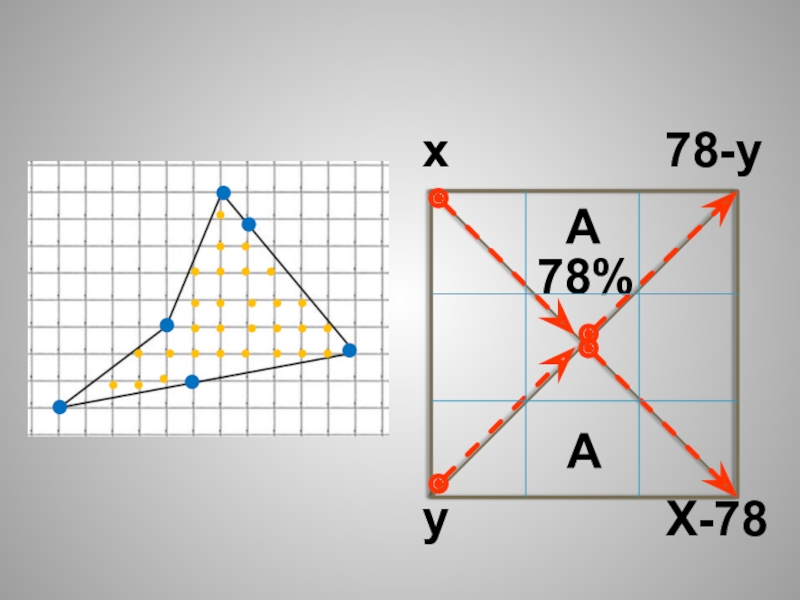
- 31. xy78%78-yX-78AA
Слайд 3Карл Пирсон
Карл Пирсон родился 27 марта 1857 в Лондоне, умер 27
Слайд 4Задачи решаемые при помощи конверта
При помощи конверта Пирсона
На смеси и сплавы
Задачи по теории вероятностей
(где встречаются проценты)
Слайд 5C-B=X
A-C=Y
A
B
C
X
Y
Q
А наибольшее число.
В наименьшее.
С число которое нужно
получить (уже дано).
P,Q количество веществ.
Суть метода
Вот как это делается
P
Слайд 6 Задача 1
70%
9%
30%
21
40
Сколько частей 9% и 70% уксуса нужно взять, чтобы
Решение
70-30=40
30-9=21
Ответ: 21 часть 70% и 40 частей 9%
Слайд 7 Задача 2
19,33%
0,63%
5,8%
5,17
13,53
При обработке молока жирностью 5,8%, получили творог и сыворотку
Сколько кг творога получили при обработке 17,8кг молока?
Решение
19,33-5,8=13,53
5,8-0,63=5,17
Ответ:5,17
Слайд 8Стандартное решение
Пусть Хг - масса творога
Yг – масса сыворотки
Тогда:
х+у=18,7
1933х+63у=187*58
у=18,7-х
1933х+63(18,7-х)=187*58
1870х+1178,1=10846
1870х=9667,9
Х=9667,9/1870
Х=5,17
Слайд 9Задача 3
25%
0%
C
С
25-с
В 4л 25% раствора некоторого вещества добавили 6л воды. Сколько
4:6=с:(25-с)
6с=4(25-с)
6с=100-4с
6с+4с=100
10с=100
С=100:10
С=10
Ответ: 10%
4л
6л
Слайд 10Задача 4
30%
15%
C
С-15
30-с
4л
6л
Смешали 4л 30% водного раствора некоторого вещества с 6л 15%
Решение
4:6=(с-15):(30-с)
4*(30-с)=6*(с-15)
120-4с=6с-90
120+90=6с+4с
210=10с
С=210:10
С=21
Ответ:21%
Слайд 11Задача 5
40%
5%
25%
20
15
175-х
х
Имеется два сплава. Первый содержит 5% никеля, второй 40%. Из
Решение
(175-X):х=20:15
15(175-х)=20х
2625-15х=20х
2625=20х+15х
2625=35х
Х=2625:35
х=75
175-75=100
Ответ: 100кг
Слайд 12Задача 6
13%
5%
11%
6
2
Первый сплав содержит 5% меди, второй 13%. Масса второго сплава
Решение
(х+3):х=6:2
2(х+3)=6х
2х+6=6х
6=6х-2х
6=4х
х=6:4
Х=1,5
1,5+(1,5+3)=6
Ответ: 6кг
х+3
х
Слайд 13Стандартное решение этой задачи
I сплав
X кг – 100%
Медь ? кг –
III сплав
X+Y кг – 100%
Медь 0,05х+0,13у – 11%
II сплав
Y кг – 100%
Медь ? кг – 13%
у-х=3
11(х+у)=100(0,05х+0,13у)
у=х+3
11х+11у=5х+13у
11х+11(х+3)=5х+13(х+3)
22х+33=18х+39
22х-18х=39-33
4х=6
х=6/4
х=1,5
у=4,5
4,5+1,5=6
Слайд 14Задачи по теории вероятностей
40%
20%
35%
15
5
Ответ: 0,75
Агрофирма закупает яйца в двух домашних хозяйствах.
Решение
Пусть х искомая вероятность того, что купленное яйцо из I хозяйства. Тогда 1-х вероятность того, что оно из II хозяйства.
х:(1-х)=15:5 х:(1-х)=3:1
х=3(1-х) х=3-3х
4х=3
х=3:4
х=0,75
х
1-х
Слайд 15Задача 7
100 : 20=(72-Y) : (X-72)
5= (72-Y) : (X-72)
72-Y=5X-360
A : A=(78-Y)
1= (78-Y) : (X-78)
78-Y = X-78
Имеется два сосуда. I содержит 100кг, а II 20кг раствора кислоты различной концентрации. При их смешивании получается раствор 72% кислоты, если смешать их в равных количествах, то получится 78% кислоты. Сколько кг кислоты в I?
72-Y=5X-360
78-Y = X-78
78-Y-72+Y=X-78-5X+360
6=282-4X
4X=276
X=276 : 4
X= 69
Ответ: 69кг кислоты
Слайд 17Георг Пик
Австрийский математик Георг Александр Пик родился 10 августа 1859 года в Вене,
Слайд 18Суть метода
Для вычисления площади многоугольника на клетчатой бумаге,
В + Г/2 − 1 где,
где В это количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника
Слайд 19Задача 1
Г = 15 (обозначены оранжевым)
В =
S=34+15/2-1=40,5 см2
Ответ: 40,5 см2
Слайд 20Задача 2
Г = 18 (обозначены оранжевым)
В =
S=20+18/2-1=28см2
Ответ:28см2
Слайд 24Метод рационализации при решении уравнений с модулями
(f(x) - g(x)) (f(x) + g(x)) = 0
2. │f(x)│= │g(x)│
(f(x) - g(x)) (f(x) + g(x)) = 0
Слайд 27Уравнение 3
│ x2+3x│= 2(x+1)
│ x2+3x│- 2(x+1) = 0
(x2+3x+2x+2)(x2+3x-2x-2) = 0
x2+5x+2 =
D=25-8=17 x1 = 1
x1,2= x2=-2
x=
Ответ:1;
Слайд 28Заключение
Продемонстрированные методы решения задач не являются чрезвычайно сложными в освоении, но
Знание этих методов для меня весьма полезно, так как мне предстоит ещё три года обучения в школе, а затем сдача ЕГЭ, за эти три года мне не раз придётся найти площадь фигуры(нанесённой на клетчатую бумагу), решить уравнение содержащее модули, или найти концентрацию раствора и его массу (в курсе химии)
Слайд 29Литература
1. Я. И. Перельман «Занимательная математика»;
издательство «Наука». – М., 2005
2. Единый банк задач ЕГЭ
3. Интернет ресурс http://ru.wikipedia.org