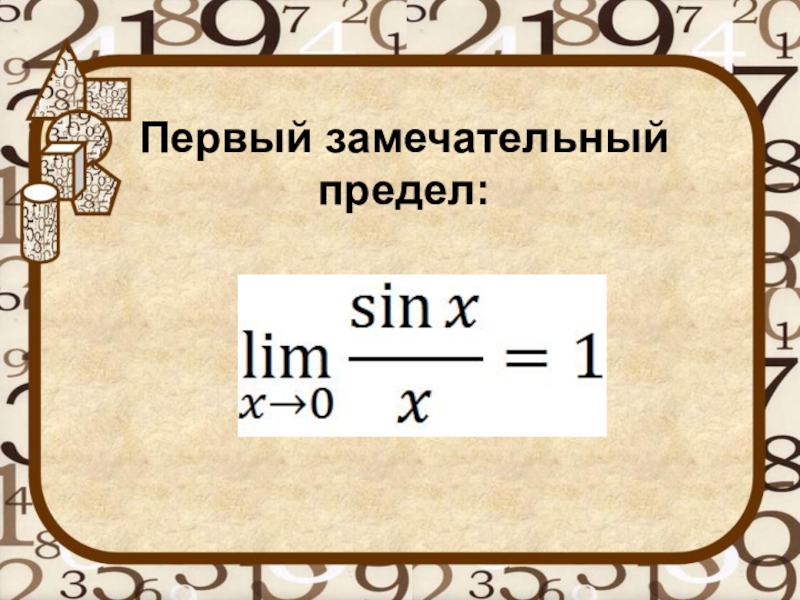- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему История пределов. Первый и второй замечательные пределы
Содержание
- 1. История пределов. Первый и второй замечательные пределы
- 2. Теория пределов Интуитивно понятие о предельном переходе при
- 3. На интуитивном уровне пределы использовали:второй половине 17
- 4. математики 18 века
- 5. Впервые определение понятия предела было введено в
- 6. Первые строгие определения предела последовательности дали:В
- 7. Дальнейшей разработкой теории пределов занималисьБернард Больцано и Карл Вейерштрасс
- 8. Замеча́тельные преде́лы - термин, использующийся в советских и
- 9. Замечательных пределов существует несколько,
- 10. Первый замечательный предел:
- 11. Огустен Луи Коши (1789 - 1857)Вывел и опубликовал доказательства предела функции
- 12. Второй замечательный предел
- 13. Якоб Бернули (1655-1705) В 1690 году Бернулли впервые
- 14. Решения задачи о предельной величине процентного дохода Если
Теория пределов Интуитивно понятие о предельном переходе при вычислении площадей и объемов различных геометрических тел использовалось еще учеными Древней Греции, особенно вработах древнегреческого математика, физика и инженера Архимеда (287 до н.э. – 212 до н.э.).
Слайд 2Теория пределов
Интуитивно понятие о предельном переходе при вычислении площадей
и объемов различных геометрических тел использовалось еще учеными Древней Греции, особенно в
работах древнегреческого математика, физика и инженера Архимеда (287 до н.э. – 212 до н.э.).
работах древнегреческого математика, физика и инженера Архимеда (287 до н.э. – 212 до н.э.).
Слайд 3На интуитивном уровне пределы использовали:
второй половине 17 века английский физик, математик
и астроном Исаак Ньютон (1642 – 1727)
Слайд 4 математики 18 века - швейцарский,
немецкий и русский математик
Леонард Эйлер (1707 - 1783) и французский математик, астроном и механик Жозеф Луи Лагранж (1736 - 1813).
Слайд 5 Впервые определение понятия предела было введено в работе Дж. Валлиса «Арифметика
бесконечных величин» (XVII век), однако исторически это понятие не лежало в основе диф-
ференциального и
интегрального
исчислений.
Слайд 6Первые строгие определения предела последовательности дали:
В 1816 году чешский математик,
философ, теолог Бернард Больцано (1781 - 1848) и французский математик Огустен Луи Коши (1789 - 1857) в 1821 году для строгого обоснования математического анализа.
Слайд 8Замеча́тельные преде́лы -
термин, использующийся в советских и российских учебниках по математическому
анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Замечательны они потому, что они уже доказаны великими математиками и нам остается лишь пользоваться ими для удобства нахождения пределов.
Слайд 9Замечательных пределов существует несколько, но самыми известными являются первый
и второй замечательные пределы. Их замечательность состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах.
Слайд 13Якоб Бернули (1655-1705)
В 1690 году Бернулли впервые
опубликовал исследование сложного процента, в
котором обосновал существование предельной выгоды, которую оценил как большую 2,5 но меньшую 3. Путём нескольких приближений он фактически искал предел последовательности
который равен числу е.
который равен числу е.
Слайд 14Решения задачи о предельной величине процентного дохода
Если исходная сумма $1 и начисляется
100%
годовых один раз в конце года, то
итоговая сумма будет $2. Но если те же самые проценты начислять два раза в год, то $1 умножается на 1,5 дважды, получая $1,00·1,52=$2,25. Начисления процентов раз в квартал приводит к $1,00·1,254=$2,44140625, и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел:
и этот предел равен числу e≈ (2,71828).
итоговая сумма будет $2. Но если те же самые проценты начислять два раза в год, то $1 умножается на 1,5 дважды, получая $1,00·1,52=$2,25. Начисления процентов раз в квартал приводит к $1,00·1,254=$2,44140625, и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел:
и этот предел равен числу e≈ (2,71828).