Слайд 1Логарифмы и логарифмическая функция в природе и технике
Подготовили ученицы 10 класса
«Б»
Семенюк Елизавета Анатольевна,
Честных Юлия Сергеевна
Руководитель: Соколова Татьяна Анатольевна, учитель математики
Муниципальное бюджетное образовательное учреждение
«Первомайская средняя общеобразовательная школа»
Первомайского района Тамбовской области
Слайд 2Проблема:
Логарифмы появились в ХVI в. под влиянием все
возрастающих потребностей практики как средство для упрощения вычислений. Нужны ли они сегодня, когда вычислительная техника достаточно развита, чтобы справляться с самыми сложными расчетами? Зачем изучают логарифмы сегодня в школе?
Слайд 3Актуальность:
Испокон веков целью математической науки было помочь людям
узнать больше об окружающем мире, познать его закономерности и тайны. Математики, выделяя самые существенные черты того или иного наблюдаемого в природе явления, вводя числовые характеристики и связывая эмпирические данные с помощью различных математических зависимостей, составляют математическую модель явления.
Слайд 4Цели:
увидеть знакомое в незнакомом;
расширить представление о логарифмической функции;
- рассмотреть применение
ее свойств в нестандартных ситуациях.
Слайд 5Выяснить:
Как возникли логарифмы?
В каких сферах жизнедеятельности человека применяются логарифмы?
Где в природе встречаются логарифмы?
Исследовать природную сущность логарифмов.
Рассмотреть практическое применение логарифмов человеком.
Задачи исследования:
Слайд 6Гипотеза:
Если математики описывают законы природы математическими символами, то они
обращаются и к логарифмической функции.
Слайд 7Основные этапы:
1.Подготовительный:
Подбор научной литературы.
Сбор информации.
2.Основной:
Обработка информации.
Создание презентации.
3. Заключительный:
Выступление на конференции.
Слайд 8История возникновения логарифма:
Михаэль Штифель
Слайд 9История
возникновения логарифма:
В 1614 году шотландский математик-любитель Джон Непер опубликовал на
латинском языке сочинение под названием «Описание удивительной таблицы логарифмов».
Слайд 10 На русском языке первые логарифмические таблицы были изданы в
1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К.Бремикера (1804-1877).
Слайд 11Логарифмическая линейка, прообразом которой явилась так называемая гантерова линейка, была изобретена
английским математиком Э.Гантером вскоре после открытия логарифмов и описана им в 1623 году . В 1630 году английский математик У. Отред заменил циркуль второй линейкой (движком).
В дальнейшем усовершенствовались лишь детали.
Слайд 12Использование логарифмической линейки в ХХl веке:
В начале
XXI века логарифмические линейки получили второе рождение в наручных часах.
Слайд 13 И только в ХХ веке Владимир Модестович Брадис придумал
способ, позволяющий до минимума сократить утомительные расчеты. Результаты расчетов представил в виде таблиц.
Слайд 14 Таким образом, прошло 400 лет с тех пор, как
впервые были введены логарифмы (считая с 1614 г.).
Понятие логарифма, логарифмической функции положено в основу школьного курса «Алгебры и начал математического анализа».
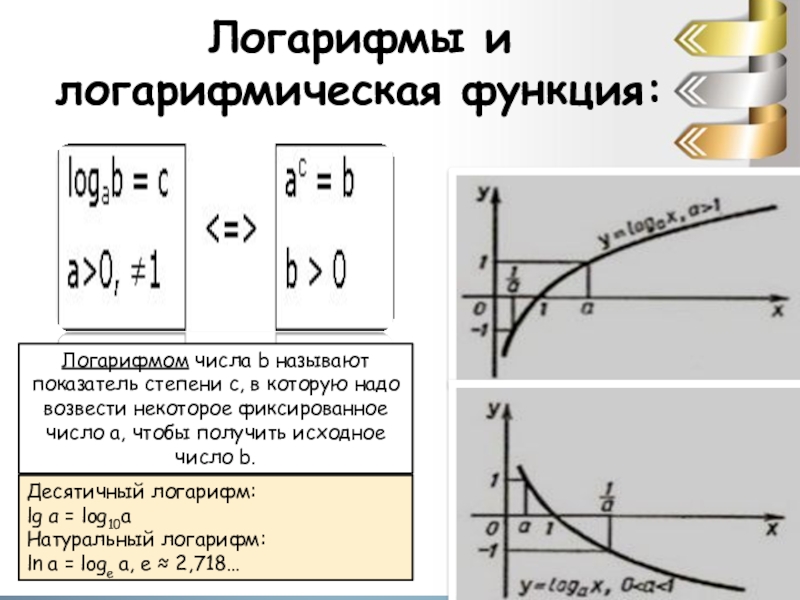
Слайд 15Логарифмы и логарифмическая функция:
Логарифмом числа b называют показатель степени c, в
которую надо возвести некоторое фиксированное число a, чтобы получить исходное число b.
Десятичный логарифм:
lg a = log10a
Натуральный логарифм:
ln a = loge a, e ≈ 2,718…
Слайд 16 Логарифмы в астрономии:
Яркость источников света - шкала звездных величин
Блеск
в астрономии — величина пропорциональная логарифму светового потока. Однако коэффициент пропорциональности отрицателен (при основании логарифма больше единицы), поэтому самым ярким объектам на небе соответствует меньшая отрицательная величина (–26,8 для Солнца), а для самых тусклых — положительная (28 для едва различимых в телескоп звезд)
Астрономы измеряют «блеск» небесных светил в звездных величинах
Слайд 17Барометрическая формула:
Давление воздуха убывает с высотой (при постоянной температуре)
по закону
где p0 – давление на уровне моря (h = 0),
p – давление на высоте h,
H – некоторая константа, зависящая от температуры.
Для температуры 200С H ≈ 7,7 м.
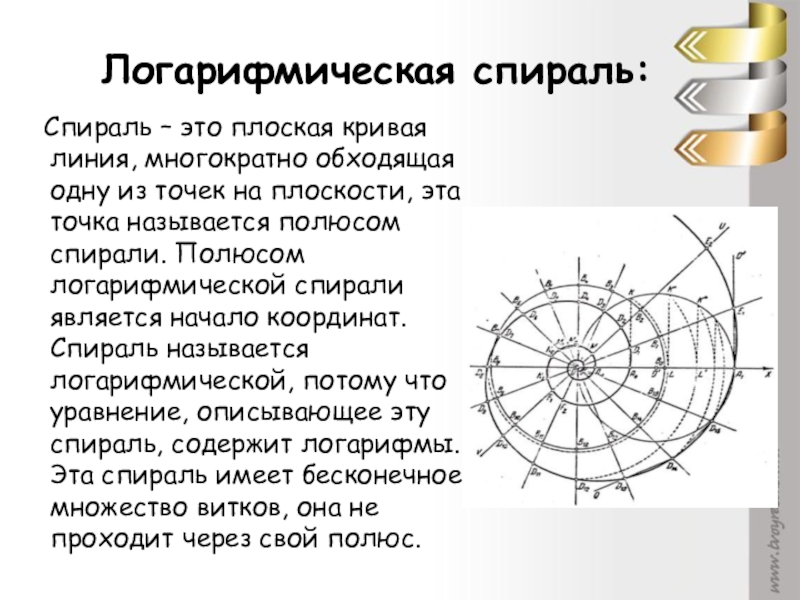
Слайд 18Логарифмическая спираль:
Спираль – это плоская кривая линия, многократно обходящая
одну из точек на плоскости, эта точка называется полюсом спирали. Полюсом логарифмической спирали является начало координат. Спираль называется логарифмической, потому что уравнение, описывающее эту спираль, содержит логарифмы. Эта спираль имеет бесконечное множество витков, она не проходит через свой полюс.
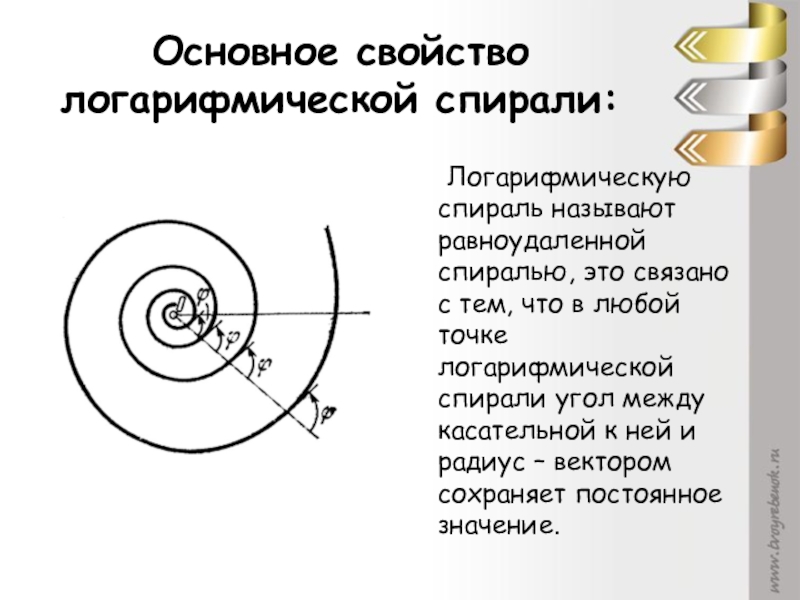
Слайд 19Основное свойство логарифмической спирали:
Логарифмическую спираль называют равноудаленной спиралью,
это связано с тем, что в любой точке логарифмической спирали угол между касательной к ней и радиус – вектором сохраняет постоянное значение.
Слайд 20Почему в качестве примера логарифмической зависимости в природе выбрали именно логарифмическую
спираль?
Слайд 21Раковины многих моллюсков, улиток, а также рога горных козлов закручены по
логарифмической спирали
Слайд 22Раковина улитки:
Немецкий биолог Румблер в 1910 году выдвинул
теорию постоянного краевого угла при построении раковин улиток. Он исходил из того, что материал, из которого строятся раковины, вначале должен быть жидким, и в жидком состоянии попадает на край уже существующей части раковины где, естественно, всегда образуется постоянный краевой угол. Под этим углом жидкость затвердевает, и снова начинается та же игра.
Слайд 23 По логарифмической спирали очерчены не только раковины. Один из
наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.
Слайд 24Полет бабочки:
Ночные бабочки, которые пролетают большие расстояния, ориентируясь
по параллельным лунным лучам, инстинктивно сохраняют постоянный угол между направлением полета и лучом света.
Если они ориентируются на пламя свечи, то инстинкт их подводит, и бабочки попадают в пламя по скручивающейся логарифмической спирали.
Слайд 25Звездные галактики:
1845 г. английский астроном Лорд Росс (Уильям Парсонс) с помощью
телескопа со 180-сантиметровым металлическим зеркалом обнаружил целый класс туманностей в виде логарифмической спирали, самым ярким примером которых явилась туманность в созвездии Гончих Псов.
Слайд 26Галактики, штормы и ураганы - впечатляющие примеры логарифмических спиралей.
Слайд 27Применение логарифмов в различных
сферах жизнедеятельности человека
Слайд 28Вращающиеся ножи:
Сила с которой они давят на разрезаемый материал,
зависит от угла резания. Для постоянного давления нужно, чтобы угол резания сохранял постоянное значение. Величина угла резания зависит от обрабатываемого материала.
Слайд 29Гидротурбины:
В гидротехнике по логарифмической спирали изгибают трубу, проводящую поток
воды к лопастям турбины. Благодаря такой форме трубы потери энергии на изменение направления течения в трубе оказываются минимальными и напор воды используется с максимальной производительностью.
спиральные камеры гидротурбин
Слайд 30Радиоактивный распад:
Изменение массы радиоактивного вещества происходит по формуле
,
где m0 – где масса вещества в начальный период времени t = 0, m – масса вещества в момент времени t,
T - период полураспада.
Это означает, что через время Т после начального момента времени, масса радиоактивного вещества уменьшается вдвое.
Слайд 31Народонаселение:
Изменение количества людей в стране на небольшом отрезке времени
с хорошей точностью описывается формулой
где N0 – число людей при t = 0,
N – число людей в момент t,
λ – некоторая константа.
Слайд 32Формула Циолковского:
Эта формула, связывающая скорость ракеты V с
ее массой m:
где Vr – скорость вылетающих газов, m0 – стартовая масса ракеты.
Слайд 33Звукоизоляция стен:
Коэффициент звукоизоляции стен измеряется по формуле
где p0
– давление звука до поглощения,
p – давление звука, прошедшего через стену,
А – некоторая константа, которая в расчетах принимается равной 20 децибелам.
Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, что
и p0 =10p, т.е. стена снижает давление звука в 10 раз.
Слайд 34Логарифмы в музыке:
Играя по клавишам современного рояля, музыкант
играет, собственно говоря, на логарифмах. Так называемые «ступени» темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношении к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин.
Номера клавишей рояля представляют собой логарифмы чисел – колебаний соответствующих.
Номер октавы представляет собой целую часть логарифма числа колебаний этого тона, а номер звука в данной октаве - дробную часть этого логарифма.
Слайд 35Частоту любого звука можно выразить формулой:
Логарифмируя эту формулу, получаем:
Принимая частоту самого
низкого «до» за единицу n=1 и приводя логарифмы к основанию 2, имеем:
Слайд 36Заключение:
Поистине безграничны приложения логарифмической функции и логарифмов в
самых различных областях науки и техники.
Многообразное применение функции вдохновило английского поэта Э. Брилла на написание оды о логарифмах.
Были поэты, которые упоминали логарифмы в своих стихах.
«Потому-то, словно пена,
Опадают наши рифмы
И величие степенно
Отступает в логарифмы».
(Борис Слуцкий).
Слайд 37Заключение:
В ходе исследовательской работы нашлось подтверждение словам Галилео Галилея «Великая книга
природы написана математическими символами».
Многие природные явления не могли быть изучены без понятия логарифма.
Логарифмы используются для описания природных явлений астрономами, физиками, биологами.
Понятие логарифма широко применяется человеком во многих науках.
Логарифм является инструментом для вычисления радиоактивного распада, изменения количества людей в стране, зависимости скорости ракеты от ее массы, коэффициента звукоизоляции.
Убедились, что, играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах.
Слайд 39Список
использованных источников:
Ш.А.Алимов и др. Алгебра и начала математического анализа 10-11класс,
М.Просвещение, 2013
Энциклопедический словарь юного математика/ Сост. А.П.Савин. – М.:Педагогика, 1985
Энциклопедия для детей. Т. 11. Математика. – М.: Аванта+, 1998
Большая электронная энциклопедия «Кирилл и Мефодий»: 2004
http://goldprop.ru/archives/214
http://ru.wikipedia.org/wiki/
http://images.yandex.ru