Учитель: Дутова Т.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
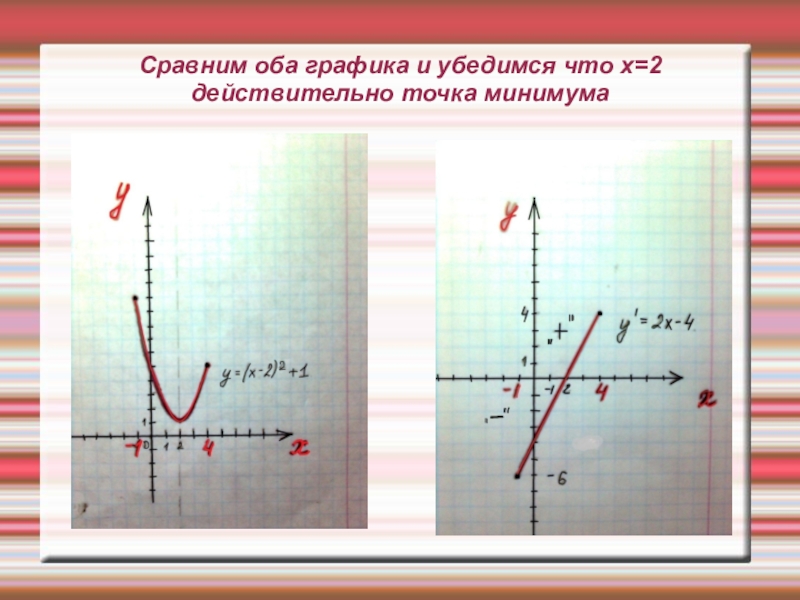
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследование функции с помощью производной
Содержание
- 1. Исследование функции с помощью производной
- 2. Слайд 2
- 3. 1) Функция убывает при Х принадлежит [-1;2]2) Функция возрастает при Х принадлежит [2;4]3) Х=2 -Точка минимума!
- 4. Найду производную данной функции: у'(х)=(х2–4х+5)'=2х-4+0=2х-4
- 5. 1) у'(х) меньше 0 на отрезке [-1;2)2)
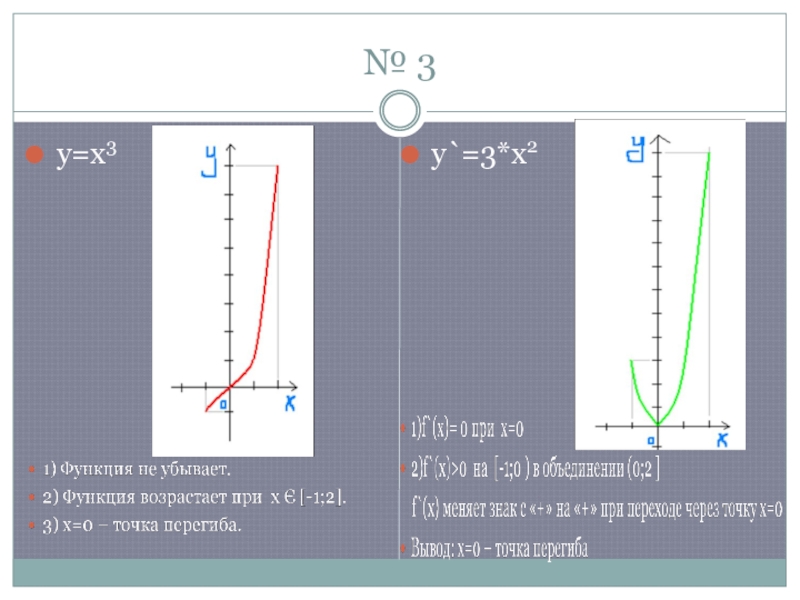
- 6. Сравним оба графика и убедимся что х=2 действительно точка минимума
- 7. ДАНА ФУНКЦИЯ А)Y=-(X+1)2 – 2, Б)
- 8. б)y= -(x+1)2 +5 на [-2;-1]Х У-2 4-1 5 0 4 1 1
- 9. а)У=-(Х+1) 2 -2Функции возрастают при хпринадлежит [-2;
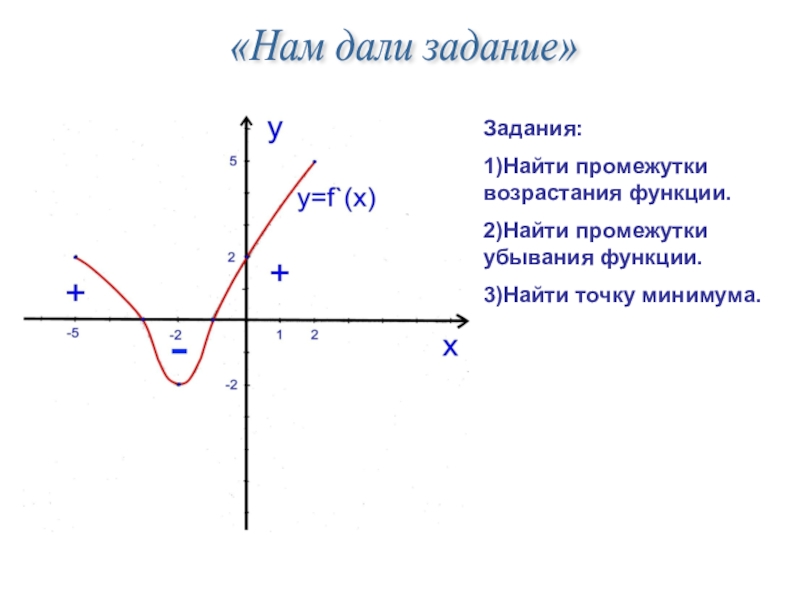
- 10. № 3y`=3*x2y=x3
- 11. «Нам дали задание» Задания:1)Найти промежутки возрастания функции.2)Найти промежутки убывания функции.3)Найти точку минимума.
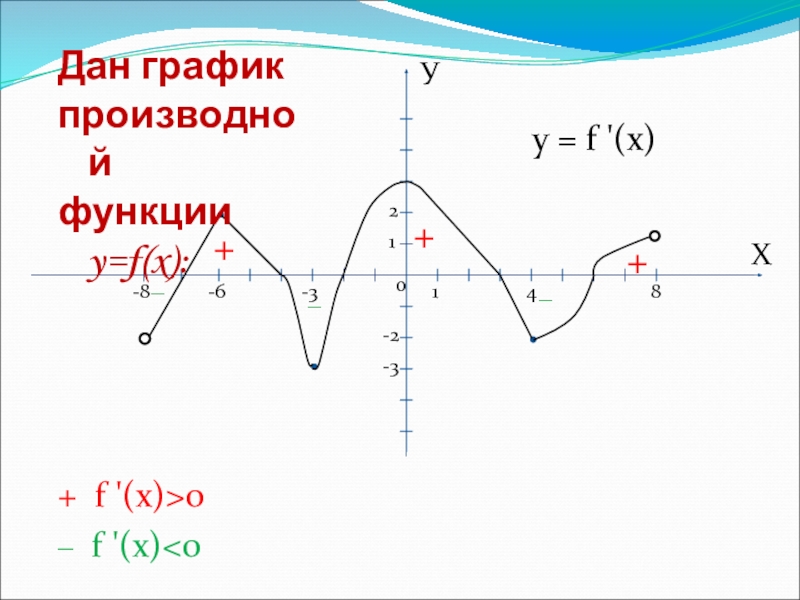
- 12. Нам дан график производной функции у =
- 13. УХ110-8-6-3-3-2248+++___+ f '(x)>0_ f '(x)
- 14. Задание №11) Найти наибольший промежуток возрастания функции.Промежутки
- 15. Задание №22) Найти сумму точек экстремума.Точки экстремума: -7;-4;-2;3;6.Сумма точек экстремума: -7+(-4)+(-2)+3+6 = -4Ответ: -4.y110х
- 16. y110хЗадание №3Найти точки максимума функции.Точки максимума: -4;3.Ответ: -4;3.
- 17. Задание №4Найти количество точек минимума функции.Точки минимума: -7;-2;6.Ответ: 3 точки минимума.y110х
- 18. Спасибо за внимание!
у=(х-2)2+1 на отрезке [-1;4] у=(х-2)2+1 раскроем формулу сокращеного умножения и получим:
Слайд 1 Презентации учащихся 10 класса МБОУ СОШ №1 на тему: "Применение производной к исследованию
функций"
Слайд 2
у=(х-2)2+1 на отрезке [-1;4]
у=(х-2)2+1 раскроем формулу сокращеного умножения и получим:
у=х2 - 4х+5– это квадратичная функция, графиком являестя парабола, ветви вверх
Найду координаты вершины параболы!
Х0 = -в/(2*а), Х0 = 2
У0 = 1
Построю график функции и исследую его...
Дополнительные точки
У(-1) = 1 +4 +5 = 10
У(4) = 16- 16 +5= 5
Слайд 3
1) Функция убывает при Х принадлежит [-1;2]
2) Функция возрастает при Х
принадлежит [2;4]
3) Х=2 -Точка минимума!
3) Х=2 -Точка минимума!
![1) Функция убывает при Х принадлежит [-1;2]2) Функция возрастает при Х принадлежит [2;4]3) Х=2 -Точка минимума!](/img/thumbs/763d4857a751b1035cdba545aa4945f5-800x.jpg "Исследование функции с помощью производной 1) Функция убывает при Х принадлежит [-1;2]2) Функция возрастает при Х принадлежит [2;4]3) Х=2 -Точка минимума!")
Слайд 4Найду производную данной функции: у'(х)=(х2–4х+5)'=2х-4+0=2х-4
Построю график функции и
исследую его...
Дополнительные точки Х | У
-1 | -6
4 | 4
Дополнительные точки Х | У
-1 | -6
4 | 4
Слайд 5
1) у'(х) меньше 0 на отрезке [-1;2)
2) у'(х) больше 0 на
отрезке (2;4]
3) 1! у'(х) = 0 при х=2
2! у'(2) меняет знак с „-“ на „+“
ВЫВОД: х=2 Точка минимума!!!
3) 1! у'(х) = 0 при х=2
2! у'(2) меняет знак с „-“ на „+“
ВЫВОД: х=2 Точка минимума!!!
![1) у'(х) меньше 0 на отрезке [-1;2)2) у'(х) больше 0 на отрезке (2;4]3) 1! у'(х) = 0](/img/thumbs/7cd6148eb1580d379d8a4f61cd3f6ca1-800x.jpg "Исследование функции с помощью производной 1) у'(х) меньше 0 на отрезке [-1;2)2) у'(х) больше 0 на")
Слайд 7ДАНА ФУНКЦИЯ А)Y=-(X+1)2 – 2,
Б) Y=-(X+1)2 +5 НА ОТРЕЗКЕ [-2;1]
а)
y= -(x+1)2-2 на [-2;1]
Х У
-3 -6
-2 -3
-1 -2
0 -3
Х У
-3 -6
-2 -3
-1 -2
0 -3
![ДАНА ФУНКЦИЯ А)Y=-(X+1)2 – 2, Б) Y=-(X+1)2 +5 НА ОТРЕЗКЕ [-2;1]а) y= -(x+1)2-2 на [-2;1] Х](/img/thumbs/3fefdcf56ad66d540fa7c250617b1c73-800x.jpg "Исследование функции с помощью производной ДАНА ФУНКЦИЯ А)Y=-(X+1)2 – 2, Б) Y=-(X+1)2 +5 НА ОТРЕЗКЕ [-2;1]а)")
![б)y= -(x+1)2 +5 на [-2;-1]Х У-2 4-1 5 0 4 1 1](/img/thumbs/a492d5dd94d30259db8d1ce6023eabc6-800x.jpg "Исследование функции с помощью производной б)y= -(x+1)2 +5 на [-2;-1]Х У-2 4-1 5 0 4 1 1")
Слайд 9а)
У=-(Х+1) 2 -2
Функции возрастают при х
принадлежит [-2; -1]
-4
f’(x)>0 на [-2;-1)
2) Функции
убывают при х
принадлежит [-1;1]
принадлежит [-1;1]
3) х=-1 – точка максимума
2) f’(x)<0 на (-1;1]
3) a) f’(x)=0 при x=-1
б) f’(-1) меняет знак с «+» на «-»
Вывод: х=-1 – точка максимума
y=-(x+1)2+5
y’=-2x-2
![а)У=-(Х+1) 2 -2Функции возрастают при хпринадлежит [-2; -1]-4f’(x)>0 на [-2;-1)2) Функции убывают при хпринадлежит [-1;1]3) х=-1 –](/img/thumbs/5ab6c627ae8c04619203f5838d34afa4-800x.jpg "Исследование функции с помощью производной а)У=-(Х+1) 2 -2Функции возрастают при хпринадлежит [-2; -1]-4f’(x)>0 на [-2;-1)2) Функции")
Слайд 11«Нам дали задание»
Задания:
1)Найти промежутки возрастания функции.
2)Найти промежутки убывания функции.
3)Найти точку
минимума.
Слайд 12
Нам дан график производной функции у = f`(х) на [-5;2]
f`(x)
0 на (-3;-1), значит функция убывает при Х Є [-3;-1]
f`(х) > 0 на (-5;-3) и (-1;2), значит функция возрастает при Х Є [-1;2] и при Х Є [-5;-3]
График производной функции пересекает ось ОХ в двух точках: x= -3; x=-1
f`(-3) меняет знак с «+» на «-», значит х=-3 точка максимума
f`(-1) меняет знак с «-» на «+», значит х=-1 точка минимума
Ответ: функция убывает при Х Є [-3;-1]
функция возрастает при Х Є [-5;-3] и при Х Є [-1;2]
Х=-1 точка минимума
f`(х) > 0 на (-5;-3) и (-1;2), значит функция возрастает при Х Є [-1;2] и при Х Є [-5;-3]
График производной функции пересекает ось ОХ в двух точках: x= -3; x=-1
f`(-3) меняет знак с «+» на «-», значит х=-3 точка максимума
f`(-1) меняет знак с «-» на «+», значит х=-1 точка минимума
Ответ: функция убывает при Х Є [-3;-1]
функция возрастает при Х Є [-5;-3] и при Х Є [-1;2]
Х=-1 точка минимума
«Вот наше решение»
![Нам дан график производной функции у = f`(х) на [-5;2]f`(x) < 0 на (-3;-1), значит функция убывает](/img/thumbs/310f1a9bf2bfff9b2b4c436603499f66-800x.jpg "Исследование функции с помощью производной Нам дан график производной функции у = f`(х) на [-5;2]f`(x) <")
Слайд 14
Задание №1
1) Найти наибольший промежуток возрастания функции.
Промежутки возрастания: [-7;-4] ; [-2;3]
; [6;8).
Наибольший промежуток: [-2;3]. Его длина 5.
Ответ: 5.
Наибольший промежуток: [-2;3]. Его длина 5.
Ответ: 5.
x
y
1
1
0
![Задание №11) Найти наибольший промежуток возрастания функции.Промежутки возрастания: [-7;-4] ; [-2;3] ; [6;8).Наибольший промежуток: [-2;3]. Его длина](/img/thumbs/56f2cc15072c92223ab47cd4ab0ce70a-800x.jpg "Исследование функции с помощью производной Задание №11) Найти наибольший промежуток возрастания функции.Промежутки возрастания: [-7;-4] ; [-2;3]")
Слайд 15
Задание №2
2) Найти сумму точек экстремума.
Точки экстремума: -7;-4;-2;3;6.
Сумма точек экстремума: -7+(-4)+(-2)+3+6
= -4
Ответ: -4.
Ответ: -4.
y
1
1
0
х
Слайд 17
Задание №4
Найти количество точек минимума функции.
Точки минимума: -7;-2;6.
Ответ: 3 точки минимума.
y
1
1
0
х
