- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Иррационадык теӊдемелер. Алардын негизги түрлөрү жана чыгаруу усулдары
Содержание
- 1. Иррационадык теӊдемелер. Алардын негизги түрлөрү жана чыгаруу усулдары
- 2. Слайд 2
- 3. Автор: математика мугалими Примбердиев Ф.М.Иррационалдык тендемелер.Алардын негизги турлору жана методдору
- 4. Слайд 4
- 5. 1. Кайсы фигура ичинде
- 6. Слайд 6
- 7. 1.Кѳрсѳткүч функция бул …
- 8. 2.Кѳрсѳткүч функциянын графиги сызгыла
- 9. 3. Теңдемени жообу эмнеге барабар
- 10. 4. Логарифм деп…
- 11. 5. Логарифмди эсептегиле
- 12. 6. Логарифм теңдемесин эсептегиле
- 13. Тема: Иррационалдык тендемелер.Алардын негизги турлору жана методдору
- 14. Аныктама: Белгисизди радикалдын
- 15. Мисалдар:
- 16. «Теңдемени чыгаруу» жана «теңдеменин тамырларын табуу же
- 17. Запись на доскеАр кандай g туюнмасы жана
- 18. Иррационалдык тендемелердин чыгаруу алгоритмиТеӊдемени эки тарапты теӊ
- 19. 1. Теӊдемени чыгаргыла:сол жагы үчүнЖообу:
- 20. 2. Теӊдемени чыгаргыла: Жообу:
- 21. Чечүү: эки тарапты теӊ квадратка киргизебиз.Жообу: 2; -3.
- 22. 5.
- 23. Мисал:
- 24. Иррациондык теңдемени чыгаргыла
- 25. х2 –х-2=4х2 –х - 6=0х1=3ТекшерүүЖообу: 3; -22=2х2=
- 26. Маселени түшүнтүрүп бергиле:
- 27. Өз алдынча маселени чечкиле.Чечими:
- 28. Диофант
- 29. Слайд 29
- 30. Диофант - великий математик.Деятельность Диофанта
- 31. Диофант и
- 32. Диофант
- 33. Вклад Диофанта в развитие алгебрыДиофанта можно по
- 34. Доскада иштөө
- 35. Спасибо за внимание! До новых встреч!Актив катышканынар үчүн ыразычылыгым билдирем!
Автор: математика мугалими Примбердиев Ф.М.Иррационалдык тендемелер.Алардын негизги турлору жана методдору
Слайд 1Автор: математика мугалими
Примбердиев Ф.М.
Иррационалдык тендемелер.
Алардын негизги турлору жана методдору
Слайд 3Автор: математика мугалими
Примбердиев Ф.М.
Иррационалдык тендемелер.
Алардын негизги турлору жана методдору
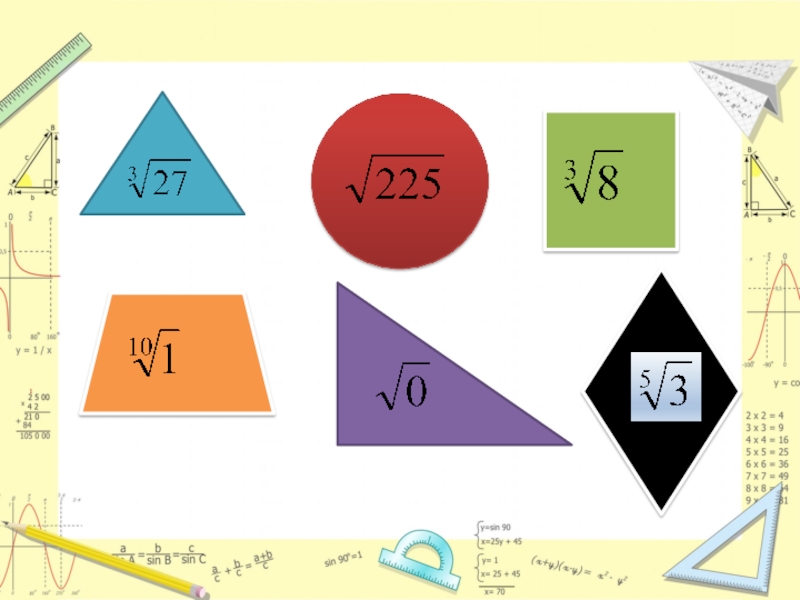
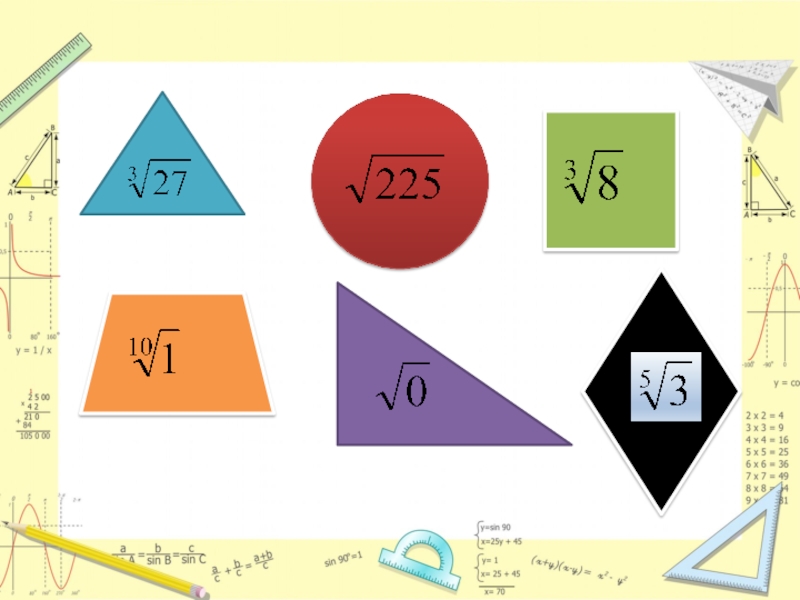
Слайд 51. Кайсы фигура ичинде жазылган? 2. Кайсы тусто
ромб берилген?
3. Торт бурчтук фигуранын ичинде
и сандын жообу канчага барабар?
4. Тегерек фигурадан кийин кайсы фигира турат?
5. Трапеция жана тик бурчтук фигураларды кошко жообу канча болот?
Слайд 14
Аныктама: Белгисизди радикалдын (тамыр белгисинин) астына камтыган
же белгисиздин рационалдык бөлчөк даражасын камтыган алгебралык теӊдеме иррационалдык теӊдеме деп аталат
Слайд 16«Теңдемени чыгаруу» жана «теңдеменин тамырларын табуу же тамыр жок экендигин далилдөө»
деген сөз айкалыштары эквивалентүү.
Теңдемени тамырын тап десе, анда анын чыныгы тамырын табуу экени түшүнүлөт
Теңдемени тамырын тап десе, анда анын чыныгы тамырын табуу экени түшүнүлөт
Теңдеменин аныкталуу облусуна тиешелүү сандар гана анын тамыры боло алат. Башка сандар тендеменин тамыры боло алышпайт;
деген теңдеменин чыгыны тамыры жок дегенди билдирет.
Слайд 18Иррационалдык тендемелердин чыгаруу алгоритми
Теӊдемени эки тарапты теӊ квадратка киргизүү.
Чыккан рационалдуу теӊдемени
чечүү.
Чыккан тамырды, берилген тендемеге коюп текшерүү.
Жоопту жазуу.
Чыккан тамырды, берилген тендемеге коюп текшерүү.
Жоопту жазуу.
Слайд 26Маселени түшүнтүрүп бергиле:
шарттарга туура келет
шарттарга туура
келбейт
Жообу: тышкы тамыр
шарттарга туура
келбейт
Жообу: тышкы тамыр
Слайд 27Өз алдынча маселени чечкиле.
Чечими:
шарртары боюнча туура келет
шарттары боюнча туура келбетй
демек, тышкы тамыр Жообу:
шарттары боюнча туура келбетй
демек, тышкы тамыр Жообу:
Слайд 30 Диофант - великий математик.
Деятельность Диофанта совпала с упадком Греции
завоеванной — как известно — Римом. Греческие ученые нашли себе убежище в Египте, главным образом в Александрии, которая к тому времени стала центром мировой культуры. В Александрии была создана великолепная библиотека, которая ко временам Диофанта стала центром мировой культуры и гуманитарных наук, в Александрии возник т. н. Мусейон (храм или святилище муз), где сосредоточилась деятельность самых выдающихся представителей естественно-математических наук. В числе этих ученых был и Диофант, математик, который, благодаря знакомству с сирийскими и индийскими математиками, перенес в греческую науку достижения вавилонян в области алгебры.
Существуют только отрывочные сведения о жизни Диофанта, нет даже данных о дне его рождения и смерти. Впрочем, некоторые подробности, к сожалению не весьма существенные, можно установить из „Эпитафии Диофанта", которую греческий монах XIV века, Максуим Плануд поместил в своей антологии.
Существуют только отрывочные сведения о жизни Диофанта, нет даже данных о дне его рождения и смерти. Впрочем, некоторые подробности, к сожалению не весьма существенные, можно установить из „Эпитафии Диофанта", которую греческий монах XIV века, Максуим Плануд поместил в своей антологии.
Слайд 31 Диофант и его труды.
Дошедший до нас
трактат греческого математика Диофанта, жившего в III веке, содержит исследование алгебраических вопросов. В своём труде он дал решение задач приводящих к так называемым диофантовым уравнениям, впервые ввёл буквенную символику в алгебру. Также в его работах мы встречаем правило знаков (минус на минус дает плюс), исследование степеней чисел и решение множества неопределенных вопросов, которые в настоящее время относятся к теории чисел.
Из 13 книг, составлявших полное собрание сочинений Диофанта, до нас дошло только 6, в которых решаются уже довольно трудные алгебраические задачи.
Из 13 книг, составлявших полное собрание сочинений Диофанта, до нас дошло только 6, в которых решаются уже довольно трудные алгебраические задачи.
Слайд 32 Диофант и его труды.
Но из
того, что осталось после Диофанта,
можно судить о его гениальных достижениях в алгебре. Ученый умел решать уравнения до третьей степени включительно, вводил в них больше неизвестных, чем это делали вавилоняне, и применял для неизвестных буквенные обозначения. Диофант пользовался специальным символом для вычитания и ввел в обиход сокращенные слова для отдельных определений и действий. Таким образом, Диофанта можно считать автором первого алгебраического языка. Например, уравнение:
в котором: „аг" (сокращение от „aritmos" — число) означает неизвестное, „то" (сокращение от „monas") единица, „is" („иол") — равняется, соответствует уравнению в нашем начертании:
Из этого примера видно, что Диофант, вместо полного словесного описания алгебраических выражений, (риторическая алгебра), ввел сокращенные обозначения.
Из 189 уравнений, которые сохранились в „Арифметике" со всей ясностью видно, что Диофант обращал главное внимание на решение положительных, рациональных неопределенных уравнений, то есть, в основном, имеющих большое число корней. Диофант интересовался, однако, только одними решениями — „положительными" и „рациональными", В поисках таких решений, Диофант проявил большую изобретательность в подборе коэффициентов, чтобы получить такое решение. Из других работ Диофанта, кроме „Арифметики" сохранились фрагменты трактата о многократных числах и отрывок рассуждений о египетской математике.
можно судить о его гениальных достижениях в алгебре. Ученый умел решать уравнения до третьей степени включительно, вводил в них больше неизвестных, чем это делали вавилоняне, и применял для неизвестных буквенные обозначения. Диофант пользовался специальным символом для вычитания и ввел в обиход сокращенные слова для отдельных определений и действий. Таким образом, Диофанта можно считать автором первого алгебраического языка. Например, уравнение:
в котором: „аг" (сокращение от „aritmos" — число) означает неизвестное, „то" (сокращение от „monas") единица, „is" („иол") — равняется, соответствует уравнению в нашем начертании:
Из этого примера видно, что Диофант, вместо полного словесного описания алгебраических выражений, (риторическая алгебра), ввел сокращенные обозначения.
Из 189 уравнений, которые сохранились в „Арифметике" со всей ясностью видно, что Диофант обращал главное внимание на решение положительных, рациональных неопределенных уравнений, то есть, в основном, имеющих большое число корней. Диофант интересовался, однако, только одними решениями — „положительными" и „рациональными", В поисках таких решений, Диофант проявил большую изобретательность в подборе коэффициентов, чтобы получить такое решение. Из других работ Диофанта, кроме „Арифметики" сохранились фрагменты трактата о многократных числах и отрывок рассуждений о египетской математике.
Слайд 33Вклад Диофанта в развитие алгебры
Диофанта можно по праву назвать «отцом алгебры»,
так как он почти всю жизнь посвятил созданию и развитию алгебры:
Ввел в обиход математические обозначения
Рассматривал дроби наравне с другими числами
Ввел в обиход «правила знаков»(минус на минус дает плюс)
Создал основу для исследования степени чисел
Ввел в обиход математические обозначения
Рассматривал дроби наравне с другими числами
Ввел в обиход «правила знаков»(минус на минус дает плюс)
Создал основу для исследования степени чисел