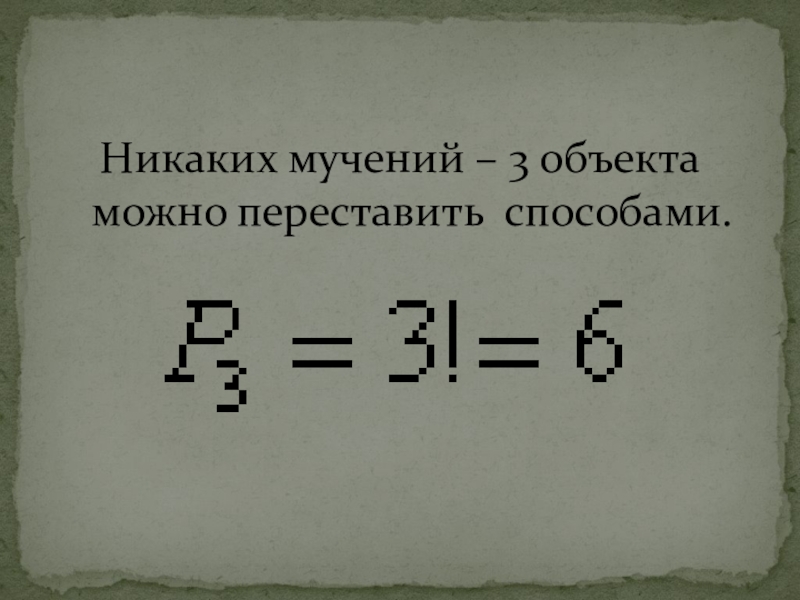- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Интуитивная комбинаторика. Доклад учащихся
Содержание
- 1. Интуитивная комбинаторика. Доклад учащихся
- 2. Комбинаторика связана со многими другими областями математики
- 3. Также комбинаторика очень нужна в повседневной жизни.
- 4. Как известно , в школе комбинаторика почти
- 5. Задачи:1. Научиться быстро анализировать комбинаторные задачи 2.
- 6. Пусть множество A состоит из k элементов : A
- 7. Общее количество различных наборов при выборе k элементов
- 8. Факториалn! = (1*2*3*4*5……..*(n-1)*n)Факториал числа n — произведение
- 9. Задачи для школьных методов Задача 1. В
- 10. Задача 2. Запишите все возможные варианты расписания
- 11. РешениеПостроим дерево возможных вариантов, обозначив М —
- 12. Задачи на комбинаторные формулыЗадача 1. Дано: яблоко
- 13. Никаких мучений – 3 объекта можно переставить способами.
- 14. Вопрос второй: сколькими способами можно выбрать а)
- 15. б) Перечислим все возможные сочетания двух фруктов:яблоко
- 16. в) И, наконец, три фрукта можно выбрать
- 17. г) Сколькими способами можно взять хотя бы один фрукт?
- 18. Вопрос третий: сколькими способами можно раздать по
- 19. Задача 2Сколько различных слов (не обязательно осмысленных)
- 20. Всё предельно просто – всего: 11 карточек,
- 21. Но предварительные комментарии о повторяющихся буквах обязательны!Ответ: 554400
- 22. Задача 3Сколько существует четырёхзначных пин-кодов?Решение: на самом
- 23. А теперь с помощью формулы. По условию
- 24. ЗаключениеВ данной работе мы изучали методы решения
- 25. Султанянов Александр и Тимербулатов ДанилСпасибо за внимание!
Комбинаторика связана со многими другими областями математики – алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний , например в школе (составление расписаний), азартных играх (подсчет частоты выигрышей), биологии (расшифровка кода ДНК),
Слайд 2Комбинаторика связана со многими другими областями математики – алгеброй, геометрией, теорией
вероятностей и имеет широкий спектр применения в различных областях знаний , например в школе (составление расписаний), азартных играх (подсчет частоты выигрышей), биологии (расшифровка кода ДНК), химии (анализ возможных связей между химическими элементами) и т.д.
Слайд 3Также комбинаторика очень нужна в повседневной жизни. Проведем небольшой эксперимент, представьте
себе что вы захотели раскрасить раскраску и у вас есть различные карандаши и некоторое количество элементов , но вы не знаете сколько способов их раскраски , а проведя обыкновенные подсчеты на листке бумаги вы с легкостью узнаете их количество. И это только один из вариантов применения комбинаторики в жизни.
Слайд 4Как известно , в школе комбинаторика почти не изучается и не
ясно почему , ведь комбинаторика -очень интересный раздел математики . В этой презентации мы бы хотели рассказать о применении комбинаторики в жизни , о том как решать различные задачи с помощью комбинаторики.
Слайд 5Задачи:
1. Научиться быстро анализировать комбинаторные задачи
2. Научиться находить возможные комбинации, составленные
из чисел, слов, предметов, отвечающие условию задачи
3. Уметь подобрать один из существующих методов для как можно более рационального решения задачи
Слайд 6 Пусть множество A состоит из k элементов : A = {a1,……,ak} ,а множество B
— из m элементов:B = {b1,…..,bm} . Тогда можно образовать ровно km пар , взяв первый элемент из A множества , а второй — из B множества .
Если в множестве n элементов, то существует ровно n! перестановок этих элементов.
Общее количество различных наборов при выборе k элементов из n с возвращением и с учётом порядка равняется nk
Если в множестве n элементов, то существует ровно n! перестановок этих элементов.
Общее количество различных наборов при выборе k элементов из n с возвращением и с учётом порядка равняется nk
Основные формулы:
Слайд 7Общее количество различных наборов при выборе k элементов из n без возвращения и без
учёта порядка равняется:
Общее количество различных наборов при выборе k элементов из n без возвращения и с учётом порядка равняется:
Например:
Общее количество различных наборов при выборе k элементов из n без возвращения и с учётом порядка равняется:
Например:
Слайд 8Факториал
n! = (1*2*3*4*5……..*(n-1)*n)
Факториал числа n — произведение всех натуральных чисел от
1 до n включительно: Например: По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Например:
7! = 1*2*3*4*5*6*7=5040
Например:
7! = 1*2*3*4*5*6*7=5040
Слайд 9Задачи для школьных методов
Задача 1.
В финальном забеге на 400 м
участвуют Алкин, Булкин и Васильев. Назовите возможные варианты распределения призовых мест.
Ответ: Вариант 1: 1)Алкин, 2)Булкин, 3)Васильев. Вариант 2: 1) Алкин, 2) Васильев, 3) Булкин. Вариант 3: 1) Васильев, 2) Алкин, 3) Булкин. Вариант 4: 1) Васильев, 2) Булкин, 3)Алкин. Вариант 5: 1) Булкин, 2) Васильев, 3) Алкин. Вариант 6: 1) Булкин, 2) Алкин, 3) Васильев.
Ответ: Вариант 1: 1)Алкин, 2)Булкин, 3)Васильев. Вариант 2: 1) Алкин, 2) Васильев, 3) Булкин. Вариант 3: 1) Васильев, 2) Алкин, 3) Булкин. Вариант 4: 1) Васильев, 2) Булкин, 3)Алкин. Вариант 5: 1) Булкин, 2) Васильев, 3) Алкин. Вариант 6: 1) Булкин, 2) Алкин, 3) Васильев.
Слайд 10Задача 2. Запишите все возможные варианты расписания факультативов на день из предметов:
моделирование, риторика, игра на гитаре, английский язык, фортепьяно, причем моделирование должно быть вторым факультативом.
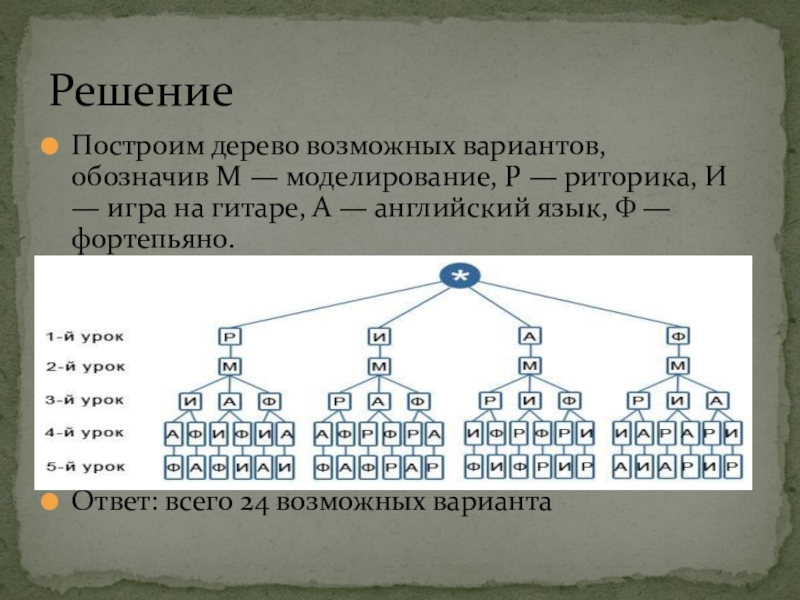
Слайд 11Решение
Построим дерево возможных вариантов, обозначив М — моделирование, Р — риторика,
И — игра на гитаре, А — английский язык, Ф — фортепьяно.
Ответ: всего 24 возможных варианта
Ответ: всего 24 возможных варианта
Слайд 12Задачи на комбинаторные формулы
Задача 1. Дано: яблоко / груша / банан
Вопрос
первый: сколькими способами их можно переставить?
Одна комбинация уже записана выше и с остальными проблем не возникает:
яблоко / банан / груша груша / яблоко / банан груша / банан / яблоко банан / яблоко / груша банан / груша / яблоко
Итого: 6 комбинаций или 6 перестановок
Одна комбинация уже записана выше и с остальными проблем не возникает:
яблоко / банан / груша груша / яблоко / банан груша / банан / яблоко банан / яблоко / груша банан / груша / яблоко
Итого: 6 комбинаций или 6 перестановок
Слайд 14Вопрос второй: сколькими способами можно выбрать а) один фрукт, б) два
фрукта, в) три фрукта, г) хотя бы один фрукт?
а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний
Запись в данном случае следует понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?»
а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний
Запись в данном случае следует понимать так: «сколькими способами можно выбрать 1 фрукт из трёх?»
Слайд 15б) Перечислим все возможные сочетания двух фруктов:
яблоко и груша;
яблоко и банан;
груша
и банан.
Количество комбинаций легко проверить по той же формуле:
Запись понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».
Количество комбинаций легко проверить по той же формуле:
Запись понимается аналогично: «сколькими способами можно выбрать 2 фрукта из трёх?».
Слайд 16в) И, наконец, три фрукта можно выбрать единственным способом:
Кстати, формула
количества сочетаний сохраняет смысл и для пустой выборки:
Этим способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё.
Этим способом можно выбрать ни одного фрукта – собственно, ничего не взять и всё.
Слайд 17г) Сколькими способами можно взять хотя бы один фрукт? Условие «хотя бы один»
подразумевает, что нас устраивает 1 фрукт (любой) или 2 любых фрукта или все 3 фрукта:
способами можно выбрать хотя бы один фрукт.
способами можно выбрать хотя бы один фрукт.
Слайд 18Вопрос третий: сколькими способами можно раздать по одному фрукту Данилу и
Саше?
Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «б» предыдущего вопроса, сделать это можно способами,
Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно пункту «б» предыдущего вопроса, сделать это можно способами,
Слайд 19Задача 2
Сколько различных слов (не обязательно осмысленных) можно получить перестановкой карточек
со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?
Решение: в том случае, если бы все буквы были различны, то следовало бы применить тривиальную формулу , однако совершенно понятно, что для предложенного набора карточек некоторые перестановки будут срабатывать «вхолостую», например, если переставить любые две карточки с буквами «К», то получится то же самое слово. Причём, физически карточки могут сильно отличаться: одна быть круглой с напечатанной буквой «К», другая – квадратной с нарисованной буквой «К». Но по смыслу задачи даже такие карточки считаются одинаковыми, поскольку в условии спрашивается о словах (а точнее, о буквосочетаниях).
Решение: в том случае, если бы все буквы были различны, то следовало бы применить тривиальную формулу , однако совершенно понятно, что для предложенного набора карточек некоторые перестановки будут срабатывать «вхолостую», например, если переставить любые две карточки с буквами «К», то получится то же самое слово. Причём, физически карточки могут сильно отличаться: одна быть круглой с напечатанной буквой «К», другая – квадратной с нарисованной буквой «К». Но по смыслу задачи даже такие карточки считаются одинаковыми, поскольку в условии спрашивается о словах (а точнее, о буквосочетаниях).
Слайд 20Всё предельно просто – всего: 11 карточек, среди которых буква:
К –
повторяется 3 раза;
О – повторяется 3 раза;
Л – повторяется 2 раза;
Ь – повторяется 1 раз;
Ч – повторяется 1 раз;
И – повторяется 1 раз.
Проверка: 3 + 3 + 2 + 1 + 1 + 1 = 11, что и требовалось проверить.
различных слов (буквосочетаний) можно получить. Больше полумиллиона!
На практике вполне допустимо не записывать общую формулу и, кроме того, опускать единичные факториалы:
Проверка: 3 + 3 + 2 + 1 + 1 + 1 = 11, что и требовалось проверить.
различных слов (буквосочетаний) можно получить. Больше полумиллиона!
На практике вполне допустимо не записывать общую формулу и, кроме того, опускать единичные факториалы:
Слайд 22Задача 3
Сколько существует четырёхзначных пин-кодов?
Решение: на самом деле для разруливания задачи
достаточно знаний правил комбинаторики:
способами можно выбрать первую цифру пин-кода и способами – вторую цифру пин-кода и столькими же способами – третью и столькими же – четвёртую. Таким образом, по правилу умножения комбинаций, четырёхзначный пин-код можно составить:
способами
способами можно выбрать первую цифру пин-кода и способами – вторую цифру пин-кода и столькими же способами – третью и столькими же – четвёртую. Таким образом, по правилу умножения комбинаций, четырёхзначный пин-код можно составить:
способами
Слайд 23А теперь с помощью формулы. По условию нам предложен набор из
n=10 цифр, из которого выбираются m=4 цифры и располагаются в определенном порядке, при этом цифры в выборке могут повторяться (т.е. любой цифрой исходного набора можно пользоваться произвольное количество раз). По формуле
количества размещений с повторениями:
Ответ: 10000 способов
количества размещений с повторениями:
Ответ: 10000 способов
Слайд 24Заключение
В данной работе мы изучали методы решения комбинаторных задач с применением
школьных методов решения и комбинаторных формул. Выяснили, что школьные методы решения не рациональны и непригодны для решения задач с большим количеством данных. Мы научились выявлять тип задач и подбирать к ним наиболее рациональное решение как с помощью формул, так и с помощью логики и интуиции.