- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Готовимся к ОГЭ. Квадратные уравнения. повторение.
Содержание
- 1. Готовимся к ОГЭ. Квадратные уравнения. повторение.
- 2. Десять способов решения квадратных уравненийРешение квадратных уравнений
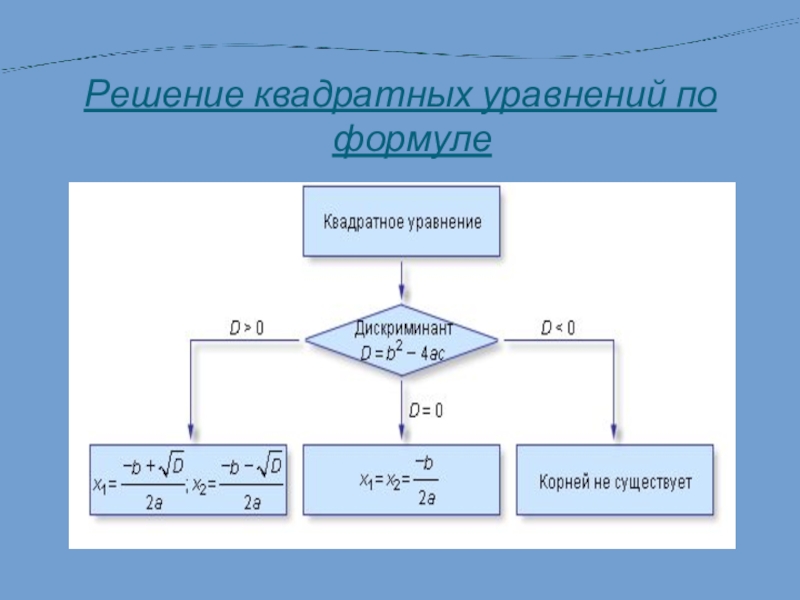
- 3. Решение квадратных уравнений по формуле
- 4. Разложение левой части уравнения на множители Этим способом
- 5. Теорема ВиетаПознакомили поэта с теоремою ВиетаОба корня
- 6. Применение свойств коэффициентов квадратного уравненияПусть дано квадратное
- 7. Метод выделения полного квадрата х2 + 6х –
- 8. Графический способ решения квадратных уравнений Решим графически уравнение
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
Десять способов решения квадратных уравненийРешение квадратных уравнений по формулеРазложение левой части уравнения на множителиТеорема ВиетаПрименение свойств коэффициентов квадратного уравненияРешение квадратных уравнений способом «переброски» старшего коэффициентаМетод выделения полного квадратаГрафический способ решения квадратных уравненийРешение квадратных уравнений с помощью
Слайд 2Десять способов решения квадратных уравнений
Решение квадратных уравнений по формуле
Разложение левой части
уравнения на множители
Теорема Виета
Применение свойств коэффициентов квадратного уравнения
Решение квадратных уравнений способом «переброски» старшего коэффициента
Метод выделения полного квадрата
Графический способ решения квадратных уравнений
Решение квадратных уравнений с помощью циркуля и линейки
Решение квадратных уравнений с помощью номограммы
Геометрический способ решения квадратных уравнений
Теорема Виета
Применение свойств коэффициентов квадратного уравнения
Решение квадратных уравнений способом «переброски» старшего коэффициента
Метод выделения полного квадрата
Графический способ решения квадратных уравнений
Решение квадратных уравнений с помощью циркуля и линейки
Решение квадратных уравнений с помощью номограммы
Геометрический способ решения квадратных уравнений
Слайд 4Разложение левой части уравнения на множители
Этим способом квадратные уравнения решаются уже
учениками седьмого класса после того как они научатся раскладывать на множители способом группировки.
Пример: х 2 + 10х – 24 = 0
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х(х + 12) – 2(х + 12) =
= (х + 12)(х – 2);
(х + 12)(х – 2) = 0;
х + 12 = 0 или х – 2 = 0;
х1 = -12 х2 = 2 ;
Числа – 12 и 2 являются корнями данного уравнения.
Ответ: х1 = -12 ; х2 = 2.
Пример: х 2 + 10х – 24 = 0
Разложим левую часть уравнения на множители:
х2 + 10х – 24 = х2 + 12х – 2х – 24 = х(х + 12) – 2(х + 12) =
= (х + 12)(х – 2);
(х + 12)(х – 2) = 0;
х + 12 = 0 или х – 2 = 0;
х1 = -12 х2 = 2 ;
Числа – 12 и 2 являются корнями данного уравнения.
Ответ: х1 = -12 ; х2 = 2.
Слайд 5Теорема Виета
Познакомили поэта с теоремою Виета
Оба корня он сложил, минус p
он получил.
А корней произведенье дает q из уравнения.
Корни приведенного квадратного уравнения
x2 + px + q = 0.
удовлетворяют теореме Виета, которая имеет вид
х1x2 = q
x1+x2 = -p
А корней произведенье дает q из уравнения.
Корни приведенного квадратного уравнения
x2 + px + q = 0.
удовлетворяют теореме Виета, которая имеет вид
х1x2 = q
x1+x2 = -p
Слайд 6Применение свойств коэффициентов квадратного уравнения
Пусть дано квадратное уравнение ах2 + bх
+ с = 0
Если а + b + с = 0 (т.е. сумма коэффициентов
уравнения равна нулю), то х1= 1, х2 = c/а
Если а - b + с = 0, или b = а + с, то х1= – 1, х2 = – с/а.
Если а + b + с = 0 (т.е. сумма коэффициентов
уравнения равна нулю), то х1= 1, х2 = c/а
Если а - b + с = 0, или b = а + с, то х1= – 1, х2 = – с/а.
Слайд 7Метод выделения полного квадрата
х2 + 6х – 7 = 0
Выделим в
левой части полный квадрат. Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2· х ·3
В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2· х ·3 + 32 = (х + 3)2
Преобразуем теперь левую часть уравнения х2 + 6х – 7 = 0, прибавляя к ней и вычитая 32, имеем:
х2 + 6х – 7 = х2 + 2· х ·3 + 32 – 32 – 7 =
= (х + 3)2 – 9 – 7 = (х + 3)2 – 16
Таким образом, данное уравнение можно записать так:
(х + 3)2 –16 = 0, т.е. (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0 или х + 3 + 4 = 0
х1 = 1 х2 = -7
Ответ: -7; 1.
х2 + 6х = х2 + 2· х ·3
В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2· х ·3 + 32 = (х + 3)2
Преобразуем теперь левую часть уравнения х2 + 6х – 7 = 0, прибавляя к ней и вычитая 32, имеем:
х2 + 6х – 7 = х2 + 2· х ·3 + 32 – 32 – 7 =
= (х + 3)2 – 9 – 7 = (х + 3)2 – 16
Таким образом, данное уравнение можно записать так:
(х + 3)2 –16 = 0, т.е. (х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0 или х + 3 + 4 = 0
х1 = 1 х2 = -7
Ответ: -7; 1.
Слайд 8Графический способ решения квадратных уравнений
Решим графически уравнение ах2 + bx +с
= 0
Постоим графики функций y = ax2 и y = - bx - c в одной системе координат
х1 и х2 – корни уравнения ах2 + bx +с = 0
Постоим графики функций y = ax2 и y = - bx - c в одной системе координат
х1 и х2 – корни уравнения ах2 + bx +с = 0