- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрическая вероятность
Содержание
- 1. Геометрическая вероятность
- 2. Мы научились вычислять вероятность событий в опытах,
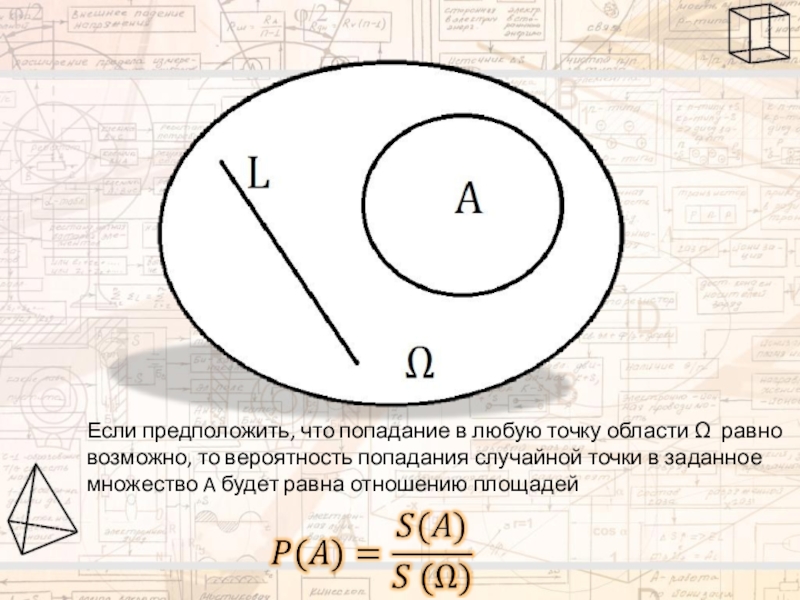
- 3. Если предположить, что попадание в любую точку
- 4. Через P мы, как и раньше, обозначаем
- 5. Опыт 1.Проводится опыт с вертушкой (рулеткой), изображенной
- 6. С какой вероятностью стрелка вертушки остановиться на
- 7. Опыт 2.В квадрат со стороной 4 см
- 8. Опыт 3.Задача о встрече. Коля и Оля
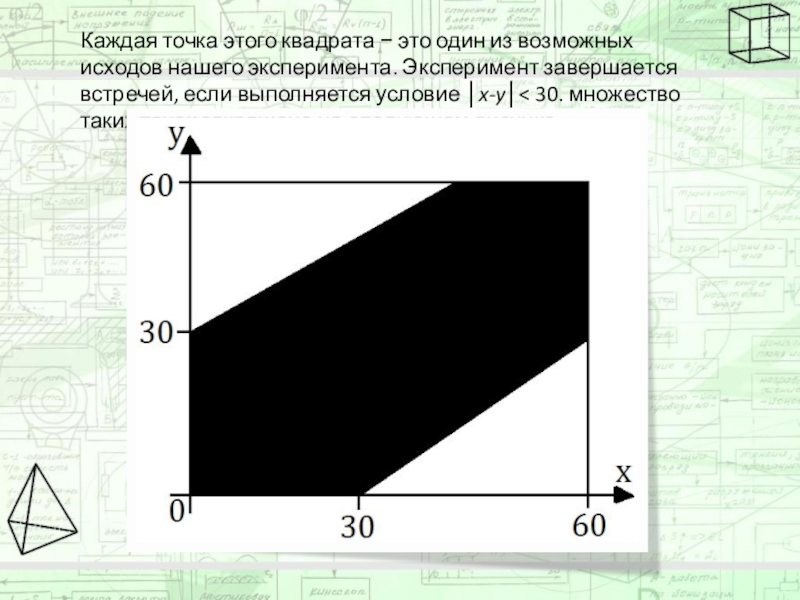
- 9. Каждая точка этого квадрата − это один
- 10. Площадь закрашенной части можно найти, вычитая из
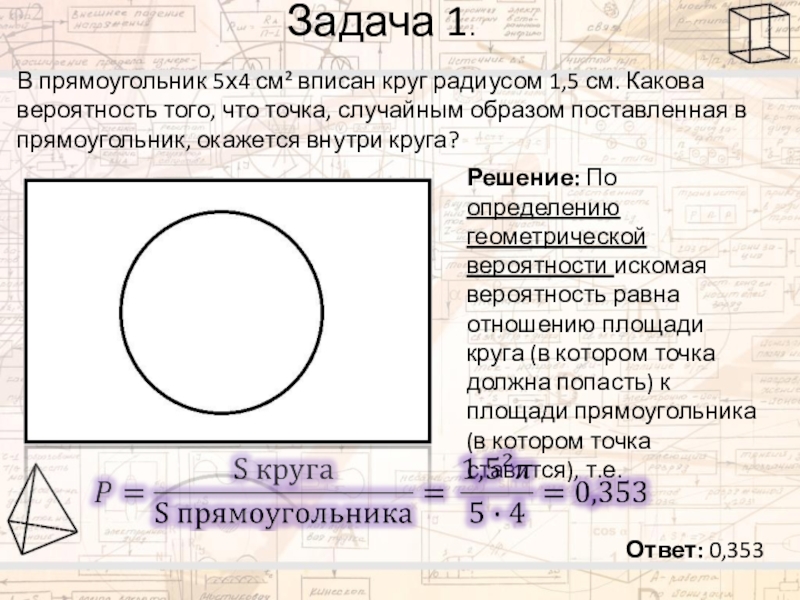
- 11. Задача 1.В прямоугольник 5х4 см² вписан круг
- 12. Задача 2.Какова вероятность Вашей встречи с другом,
- 13. Тогда вероятность встречи равна отношению площадей области G, то есть P(A)=SGSOABC=60·60-55·5560·60=23 144=0,16. Ответ: 0,16
- 14. Задача 3.Оконная решетка состоит из клеток со
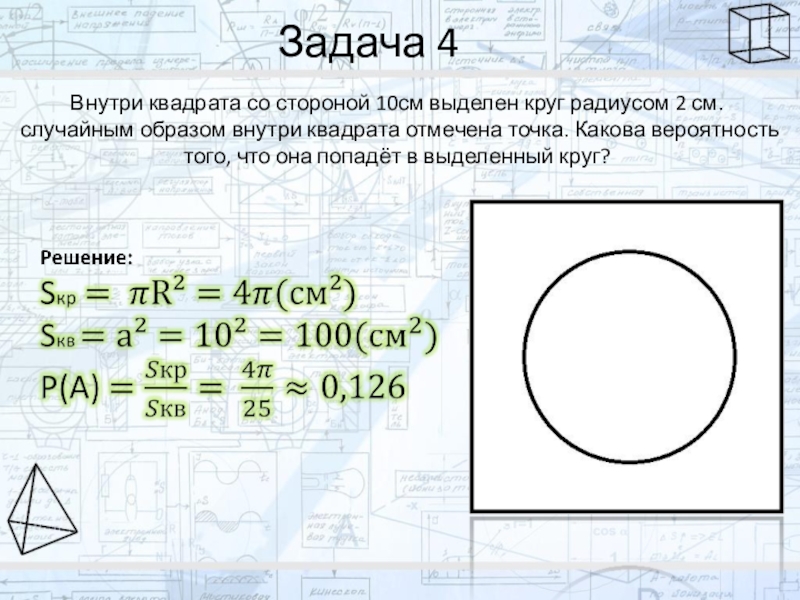
- 15. Задача 4Внутри квадрата со стороной 10см выделен
- 16. Спасибо за внимание.
Слайд 2Мы научились вычислять вероятность событий в опытах, имеющих конечное число равновозможных
А как быть, если этих исходов бесконечно много? Такая ситуация возникает в некоторых геометрических задачах, связанных со случайным выбором точки на прямой, плоскости или в пространстве. Формула классической вероятности здесь уже неприменима. Посмотрим, как всё же в том случае вычислить вероятность без обращения к опыту.
Выберем на географической карте мира случайную точку (например зажмурим глаза и покажем указкой). Какова вероятность, что эта точка окажется в России? Очевидно, для ответа на вопрос нужно знать, какую часть всей карты занимает Россия. Точнее какую часть всей площади карты составляет Россия. Отношение этих площадей и даст искомую вероятность. А какова вероятность попасть при этом в Гринвичский меридиан? Как ни странно, придётся положить её равной нулю, т.к. площадь меридиана равна нулю (это ведь линия, а не фигура: у неё есть только длина). На самом деле ничего странного в этом факте нет − попасть указкой точно в меридиан невозможно.
Такую же картинку мы имеем и в общем случае, когда в некоторой ограниченной области Ω случайно выбирается точка:
Слайд 3Если предположить, что попадание в любую точку области Ω равно возможно,
Слайд 4Через P мы, как и раньше, обозначаем вероятность, а через S
Ситуация напоминает классическое определение вероятности: как и здесь, важна равно возможность всех исходов, т.е. всех точек области, но теперь число исходов эксперимента бесконечно, поэтому приходится считать не их количество, а занимаемую ими площадь. Точно так можно определить геометрическую вероятность в пространстве (вместо площадей здесь надо брать объемы тел) и на прямой (а здесь − длины отрезков).
Слайд 5Опыт 1.
Проводится опыт с вертушкой (рулеткой), изображенной на рисунке. В центре
Слайд 6С какой вероятностью стрелка вертушки остановиться на черном секторе?
Для ответы на
где a − центральный угол дуги, выраженный в радианах. Отсюда искомая вероятность будет
Слайд 7Опыт 2.
В квадрат со стороной 4 см «бросают» точку. Какова вероятность
Изобразим квадрат со стороной 4 см и закрасим в нём множество точек удалённых от ближайшей стороны квадрата меньше, чем на 1 см:
Площадь закрашенной части квадрата составляет 16см² - 4см² = 12см². отсюда искомая вероятность будет
В заключении рассмотрим опыт, который на первый взгляд не имеет отношения к геометрической вероятности.
Слайд 8Опыт 3.
Задача о встрече. Коля и Оля договорились встретиться в Центральном
Обозначаем время прихода в парк Коли через x, а Оли − через y (для удобства будем выражать время в минутах, прошедших после 12часов). Тогда точка с координатами (x, y) будет случайной точкой в квадрате на плоскости Oxy, изображенном на рисунке:
Слайд 9Каждая точка этого квадрата − это один из возможных исходов нашего
Слайд 10Площадь закрашенной части можно найти, вычитая из площади квадрата площадь двух
Искомую вероятность встречи находим как отношение «благоприятной» площади ко всей площади квадрата:
Слайд 11Задача 1.
В прямоугольник 5х4 см² вписан круг радиусом 1,5 см. Какова
Решение: По определению геометрической вероятности искомая вероятность равна отношению площади круга (в котором точка должна попасть) к площади прямоугольника (в котором точка ставится), т.е.
Ответ: 0,353
Слайд 12Задача 2.
Какова вероятность Вашей встречи с другом, если вы договорились встретиться
y-x<5, y>x,
x-y<5, x>y.
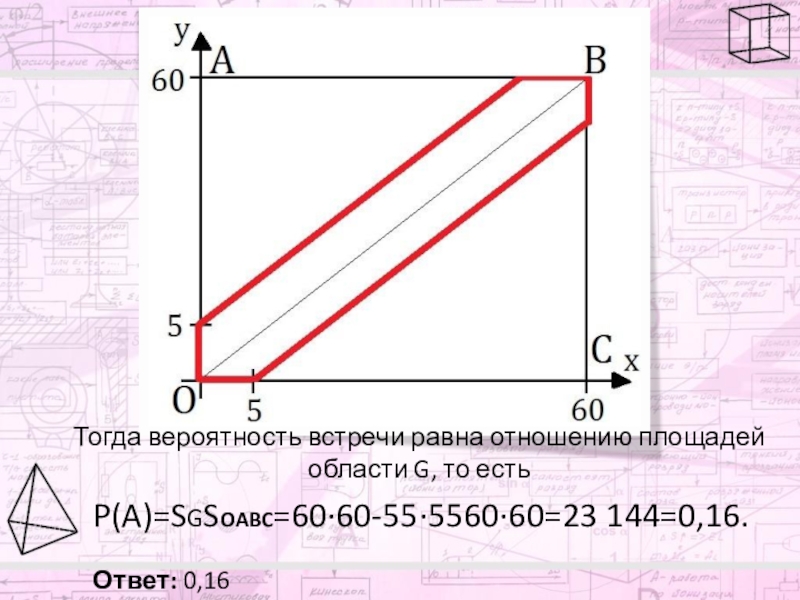
Этим неравенствам удовлетворяют точки, лежащие в области G, очерченной красным.
Слайд 13Тогда вероятность встречи равна отношению площадей области G, то есть
P(A)=SGSOABC=60·60-55·5560·60=23
Ответ: 0,16
Слайд 14Задача 3.
Оконная решетка состоит из клеток со стороной 20см. Какова вероятность
A={попавший в окно мяч, пролетит через решётку, не задев её}