- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему ФУНКЦИОНАЛЬНО - ГРАФИЧЕСКИЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ С ПАРАМЕТРАМИ
Содержание
- 1. ФУНКЦИОНАЛЬНО - ГРАФИЧЕСКИЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ С ПАРАМЕТРАМИ
- 2. Тема урока:ФУНКЦИОНАЛЬНО - ГРАФИЧЕСКИЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧ С ПАРАМЕТРАМИ
- 3. Если вы хотите научиться
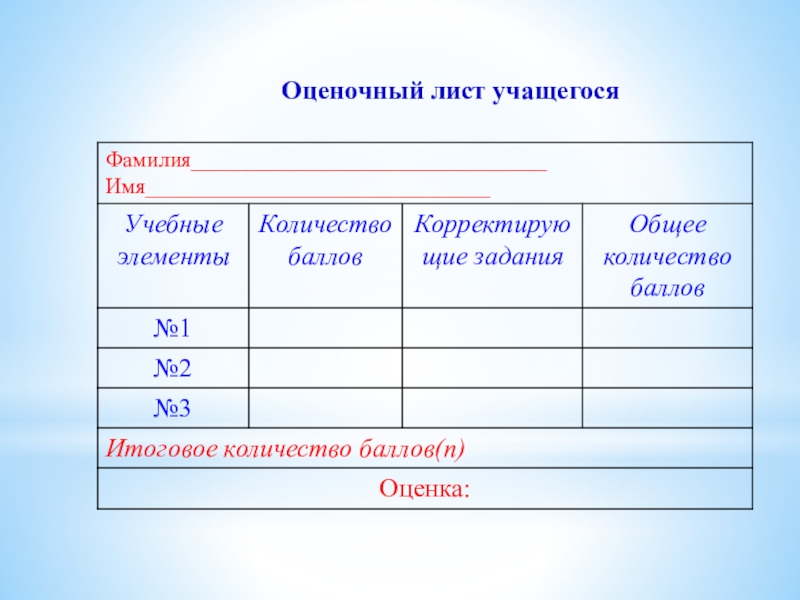
- 4. Оценочный лист учащегося
- 5. УЭ1Мотивация. Эпиграф.Актуализация опорных знаний Задание 1. Семейство функций.Объявление темы, плана.
- 6. УЭ2Повторение. Что мы знаем о параметрах.Типы задач
- 7. УЭ3Цель: научиться применить функционально - графический способ
- 8. УЭ4Цель: применять полученные знания в нестандартных и более сложных ситуациях. Пример 6. Диагностика №3.Проверка.Подведение итогов.Оценивание.
- 9. Задание 18, ЕГЭ-2016
- 10. Задание №1Построить график функции:
- 11. Задача №1
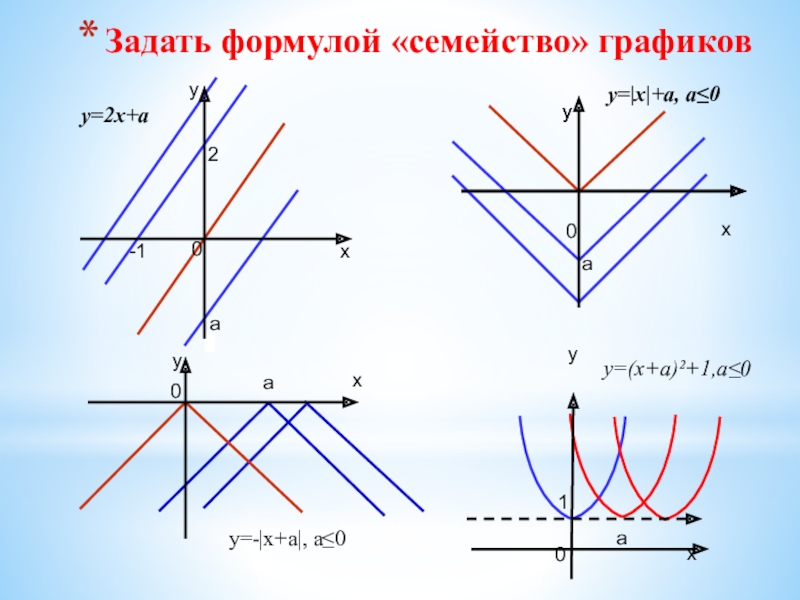
- 12. Задать формулой «семейство» графиковy=2х+аy=|х|+а, а≤0y=-|х+а|, а≤0ааа000хххууу0хауy=(х+а)²+1,а≤0у-121
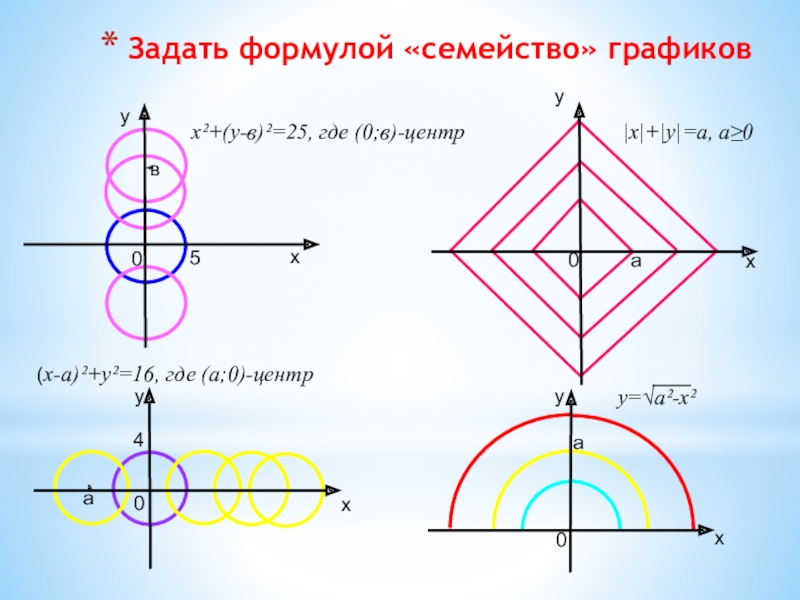
- 13. Задать формулой «семейство» графиков0ху0ху0хувх²+(у-в)²=25, где (0;в)-центра|х|+|у|=а, а≥0аy=√а²-х²0х4а(х-а)²+у²=16, где (а;0)-центру5
- 14. Определение. В уравнениях (неравенствах) коэффициенты при неизвестных
- 15. Основные типы задач с параметром Задачи, которые
- 16. Способы решения АналитическийГрафическийРешение относительно параметра
- 17. Диагностика № 1
- 18. Вариант 1Вариант 2Ответы.
- 19. Пусть дано уравнение f (x) = g
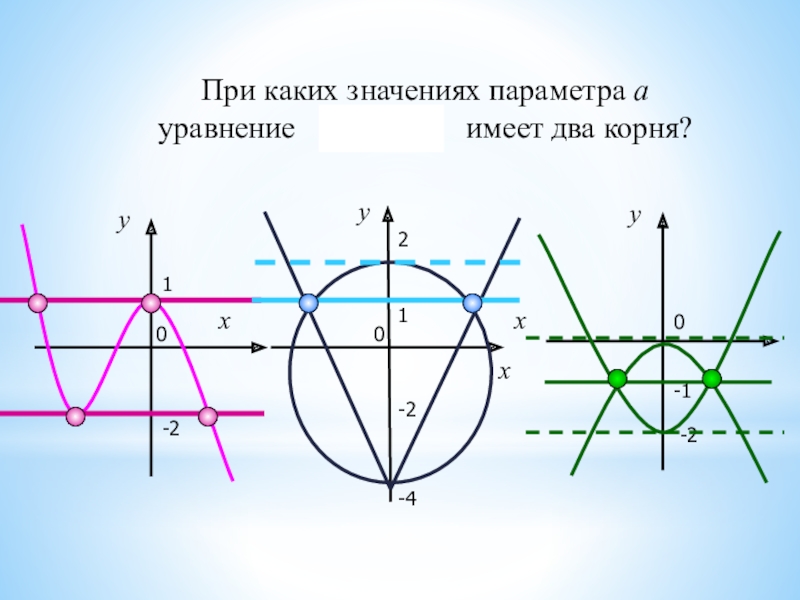
- 20. №1. При каких значениях параметра а уравнение
- 21. у1234-213При каких значениях параметра а уравнение
- 22. 2. При каких значениях параметра а уравнение
- 23. Вывод(Графический способ решения задач с параметром)Задачу с
- 24. Указать количество корней уравнения f(x)=а при всех
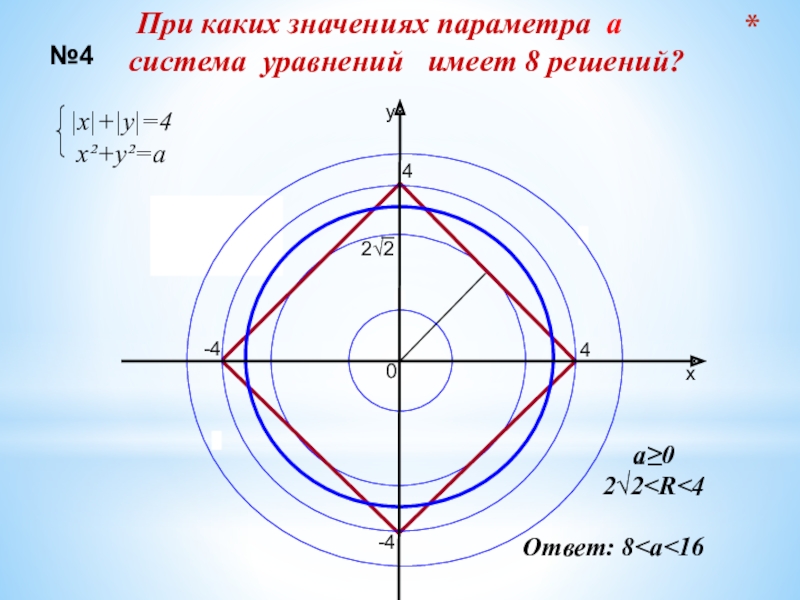
- 25. 04ху4-4-4|х|+|у|=4х²+у²=а№4Ответ: 8
- 26. При каких значениях параметра а система уравнений не имеет решений?х²-4х+у²+а²=2ау(х-5)²+(у-3)²=13542ху0(х-2)²+(у-а)²=4(х-5)²+(у-3)²=1Ответ: а≠3№5
- 27. хПри каких значениях параметра а уравнение
- 28. Диагностика№2
- 29. Проверка диагностики №20ху№1х№2Ответ: а≥7///////////////////////////////Ответ: а
- 30. 0ху0х№422Ответ: а=±44436-6Ответ: а>6, а
- 31. Задание 18, ЕГЭ-20166. демонстрационный вариант 2016
- 32. Слайд 32
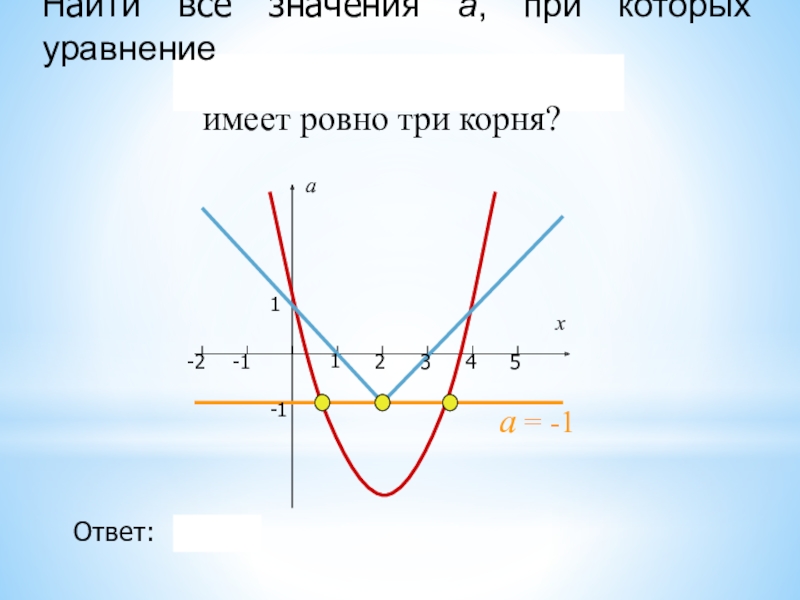
- 33. Найти все значения а, при которых уравнение имеет ровно три корня?
- 34. Оценочный лист учащегося
- 35. Критерии оценок:« 5 » - 30
- 36. “Музыка может возвышать или умиротворять душу, Живопись
Слайд 3 Если вы хотите научиться плавать, то смело входите
(Д. Пойа)
Слайд 5УЭ1
Мотивация. Эпиграф.
Актуализация опорных знаний
Задание 1.
Семейство функций.
Объявление темы, плана.
Слайд 6УЭ2
Повторение. Что мы знаем о параметрах.
Типы задач с параметрами. Способы решения.
Проверка
Самопроверка.
Слайд 7УЭ3
Цель: научиться применить функционально - графический способ при решении уравнений с
Изучение новой темы.
Примеры. №1-3.
Работа по готовым чертежам
Примеры 4-5.
Диагностика №2.
Взаимопроверка.
Слайд 8УЭ4
Цель: применять полученные знания в нестандартных и более сложных ситуациях.
Пример
Диагностика №3.
Проверка.
Подведение итогов.
Оценивание.
Слайд 12Задать формулой «семейство» графиков
y=2х+а
y=|х|+а, а≤0
y=-|х+а|, а≤0
а
а
а
0
0
0
х
х
х
у
у
у
0
х
а
у
y=(х+а)²+1,а≤0
у
-1
2
1
Слайд 13Задать формулой «семейство» графиков
0
х
у
0
х
у
0
х
у
в
х²+(у-в)²=25, где (0;в)-центр
а
|х|+|у|=а, а≥0
а
y=√а²-х²
0
х
4
а
(х-а)²+у²=16, где (а;0)-центр
у
5
Слайд 14
Определение. В уравнениях (неравенствах) коэффициенты при неизвестных или свободные члены заданные
Определение параметра
Слайд 15Основные типы задач с параметром
Задачи, которые надо решать для любого значения
Например. Решите уравнение 2|x+a|-|x-2a|=3a в зависимости от параметра a.
Задачи, для которых надо найти количество решений в зависимости от параметра.
Например. Дано уравнение |x-a| -|2x-4|=5 . Определить значения параметра a, при которых оно имеет единственное решение.
Задачи, для которых при искомых значениях параметра множество решений удовлетворяют заданным условиям
Например. При каком значении параметра a решением уравнения является множество .
Слайд 17Диагностика № 1
I вариант
1. При каких значениях
имеет два различных корня?
2. Найти все значения a , при
которых уравнение
имеет хотя бы один корень.
3. При каких значениях
параметра a , уравнение
не имеет корней?
2 вариант
1. При каких значениях параметра k, уравнение
имеет два различных корня?
2. Найти все значения р , при
которых уравнение
имеет хотя бы один корень.
3. При каких значениях
параметра m , уравнение
не имеет корней?
x2- px+p+3=0
Слайд 19Пусть дано уравнение f (x) = g (x).
Строим графики функций левой
Находим точки пересечения графиков.
Абсциссы точек пересечения и есть решения данного уравнения.
РЕШЕНИЕ УРАВНЕНИЙ
ГРАФИЧЕСКИМ СПОСОБОМ
(«Функции и графики», материалы ЕГЭ, часть «В»)
Слайд 20№1. При каких значениях параметра а уравнение
№2. При каких значениях параметра а уравнение не имеет решений ?
« Математике нельзя научиться , глядя как это делает сосед! »
А.Нивен. Канадско-американский математик, специалист в теории чисел. Родился:25 октября 1915 г., Ванкувер, Канада
Умер:9 мая 1999 г. (83 года), Юджин, Орегон, США
Слайд 21 у
1
2
3
4
-2
1
3
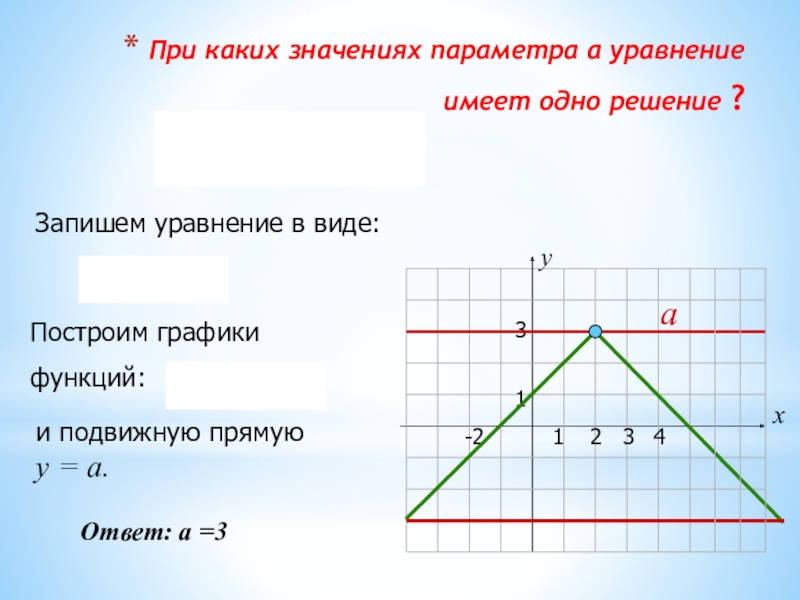
При каких значениях параметра а уравнение имеет одно решение ?
Запишем уравнение в виде:
х
Построим графики
функций:
Ответ: а =3
и подвижную прямую у = а.
а
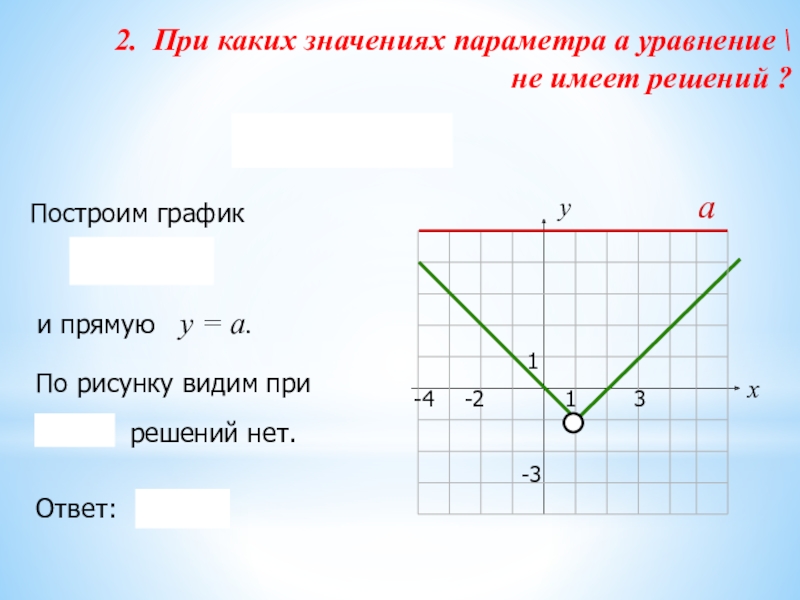
Слайд 222. При каких значениях параметра а уравнение \
не имеет решений ?
х
у
1
3
-4
1
-3
-2
Построим график
По рисунку видим при
и прямую у = а.
решений нет.
Ответ:
Слайд 23Вывод
(Графический способ решения задач с параметром)
Задачу с параметром можно рассматривать как
1. Строим графический образ
2. Пересекаем полученный график прямыми
параллельными оси абсцисс
3. «Считываем» нужную информацию
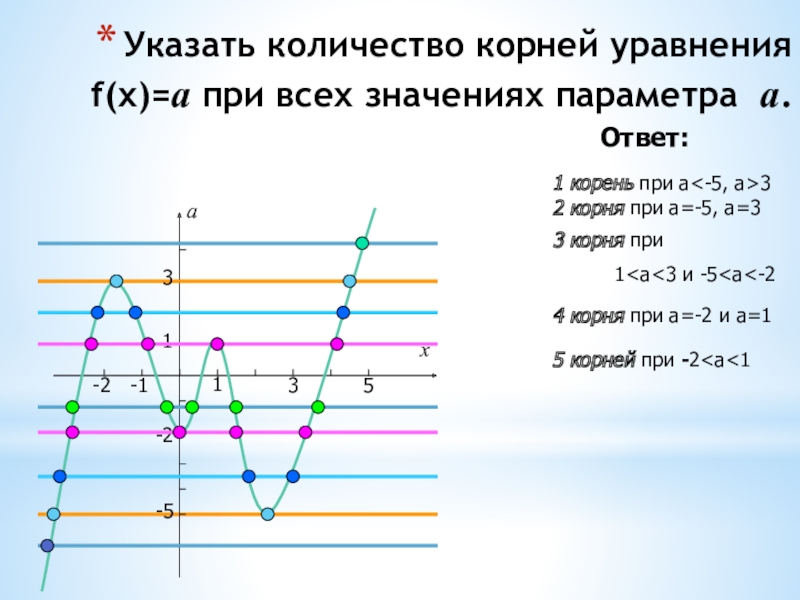
Слайд 24Указать количество корней уравнения f(x)=а при всех значениях параметра а.
1
3
5
-1
-2
1
х
а
-2
-5
3
Ответ:
1 корень
2 корня при а=-5, а=3
3 корня при 4 корня при а=-2 и а=1 5 корней при -2
1
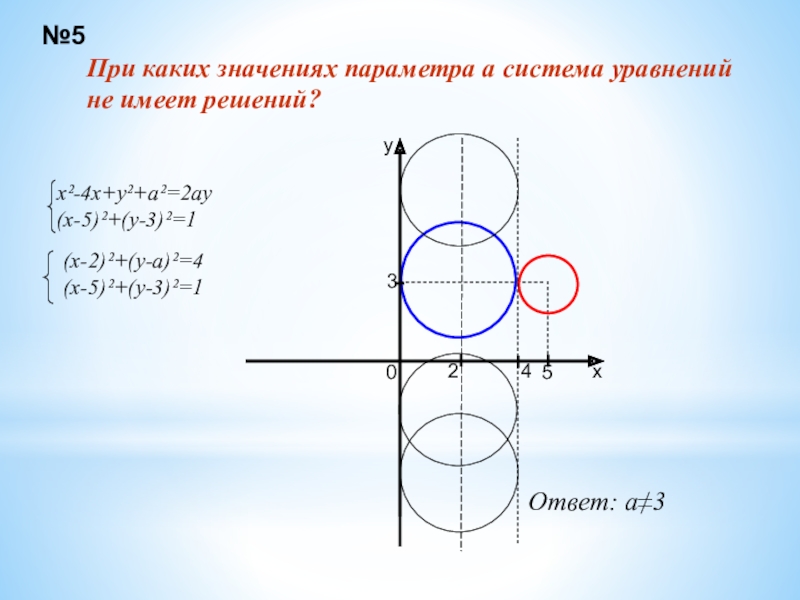
Слайд 26При каких значениях параметра а система уравнений
не имеет решений?
х²-4х+у²+а²=2ау
(х-5)²+(у-3)²=1
3
5
4
2
х
у
0
(х-2)²+(у-а)²=4
(х-5)²+(у-3)²=1
Ответ: а≠3
№5
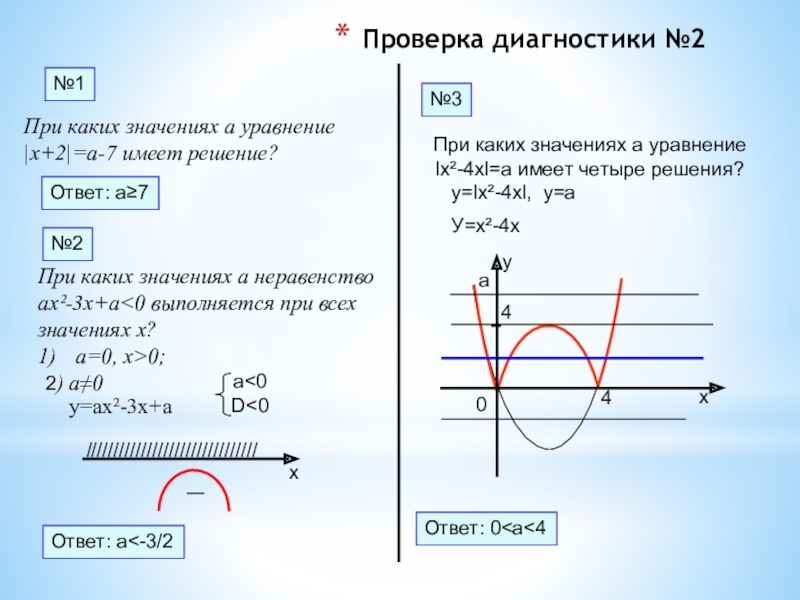
Слайд 29Проверка диагностики №2
0
х
у
№1
х
№2
Ответ: а≥7
///////////////////////////////
Ответ: а
При каких значениях а неравенство
ах²-3х+а<0 выполняется при всех
значениях х?
а=0, х>0;
2) а≠0
При каких значениях а уравнение
lх²-4хl=а имеет четыре решения?
у=ах²-3х+а
у=lх²-4хl, у=а
У=х²-4х
4
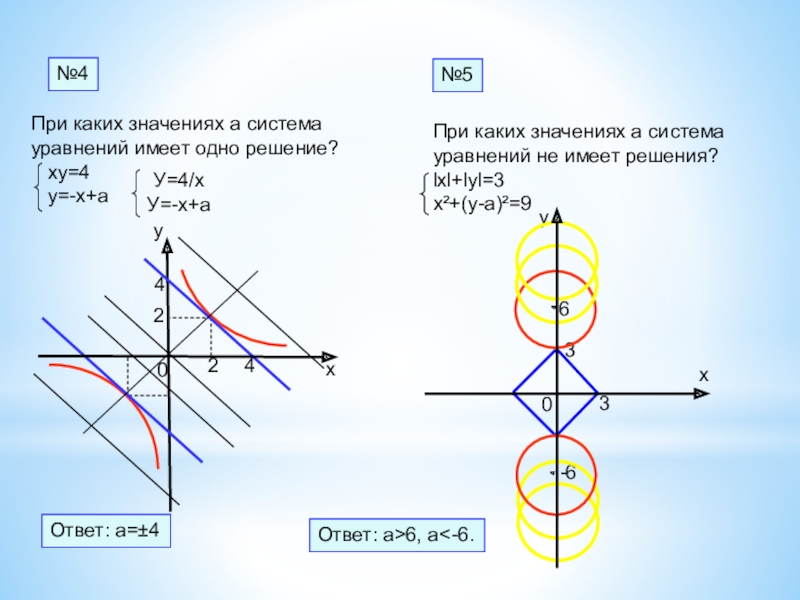
Слайд 300
х
у
0
х
№4
2
2
Ответ: а=±4
4
4
3
6
-6
Ответ: а>6, а
ху=4
у=-х+а
При каких значениях а система
уравнений не имеет решения?
lхl+lуl=3
х²+(у-а)²=9
У=4/х
У=-х+а
у
3
Слайд 36“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия -
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
а математика способна достичь всех этих целей”.
Aмериканский математик Морис Клайн.