выход
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему ЭОР: Решение логарифмических уравнений
Содержание
- 1. ЭОР: Решение логарифмических уравнений
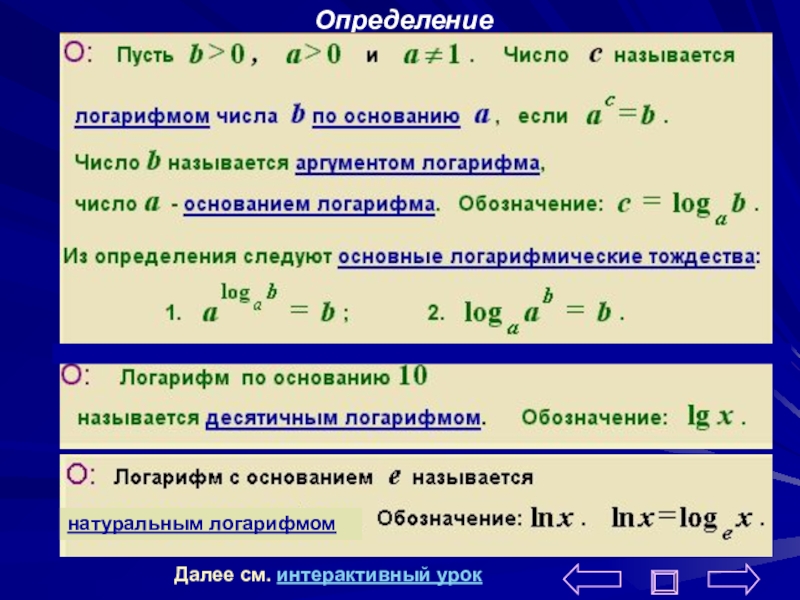
- 2. Определение логарифма Об истории
- 3. Определениенатуральным логарифмомДалее см. интерактивный урок
- 4. Определение и свойства логарифма(смотри урок-фильм)Для продолжения урока-фильма Меню - Control – Play (Ctrl+Enter)
- 5. Об истории развития логарифмов Слово логарифм происходит
- 6. Слово ЛОГАРИФМ
- 7. Гимназия № 8, г. СочиЧернобабова К.В. Джон Непер (1550-1617)
- 8. Гимназия № 8, г. СочиЧернобабова К.В.Первые таблицы
- 9. Гимназия № 8, г. СочиЧернобабова К.В.
- 10.
- 11. Логарифмическая линейка
- 12. Логарифм можно найти теперь
- 13. Основные свойства логарифмовЕсли k=2n, тоФормулы за работой
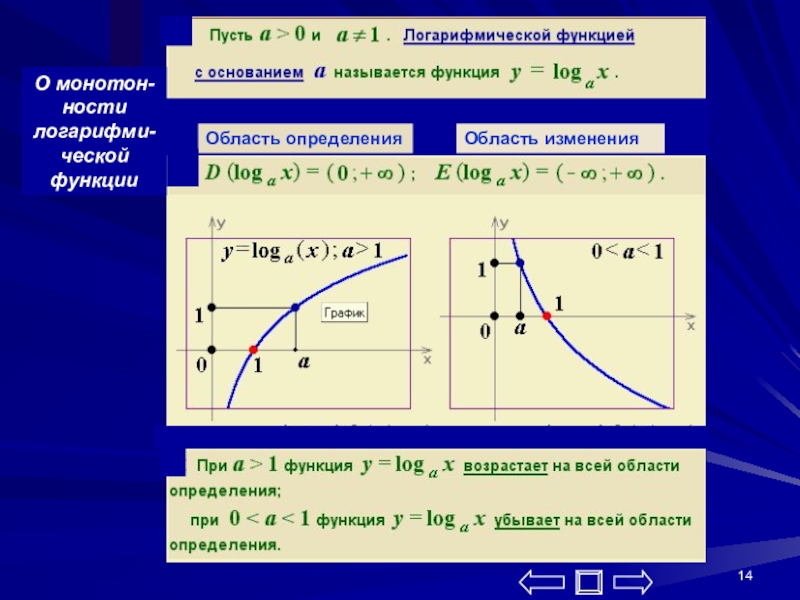
- 14. Область определенияОбласть измененияО монотон-ности логарифми-ческой функции
- 15. Уравнение видаlogaf(x) = logag(x) (или сводящееся к этому виду)называют логарифмическим
- 16. Если f(x)>0 и g(x)>0, a>0 и
- 17. 4) Сколько корней имеет уравнение? Вариант 1 Вариант 2Ответ
- 18. Методы решения логарифмических уравнений:1. Потенцирование Пример 1
- 19. Гимназия № 8, г. СочиЧернобабова К.В.Этапы решения
- 20. Гимназия № 8, г. СочиЧернобабова К.В.Вычисли устно:-231/2927==Ответы (щелкни)
- 21. Гимназия № 8, г. СочиЧернобабова К.В.Реши устно уравнения:X=27X=27X=27X=8X=2Ответы (щелкни)
- 22. Гимназия № 8, г. СочиЧернобабова К.В.1) Сравни
- 23. 4) Сколько корней имеет уравнение? Вариант 1 Вариант 2Ответ
- 24. 4) Сколько корней имеет уравнение? В1
- 25. http://www.eurekanet.ruhttp://www.college.ruhttp://www.EGE.ruВыходhttp://www.mediahouse.ru
- 26. Формулы преобразования логарифмов и их использование при
- 27. Для прослушивания речевых комментариев необходимо иметь наушники
- 28. Существует несколько методических подходов к
- 29. А чем плох второй
- 30. Еще раз о третьем подходе к решению логарифмических уравнений(«Готовимся к ЕГЭ» В.Н. Студенецкая)
- 31. Слайд 31
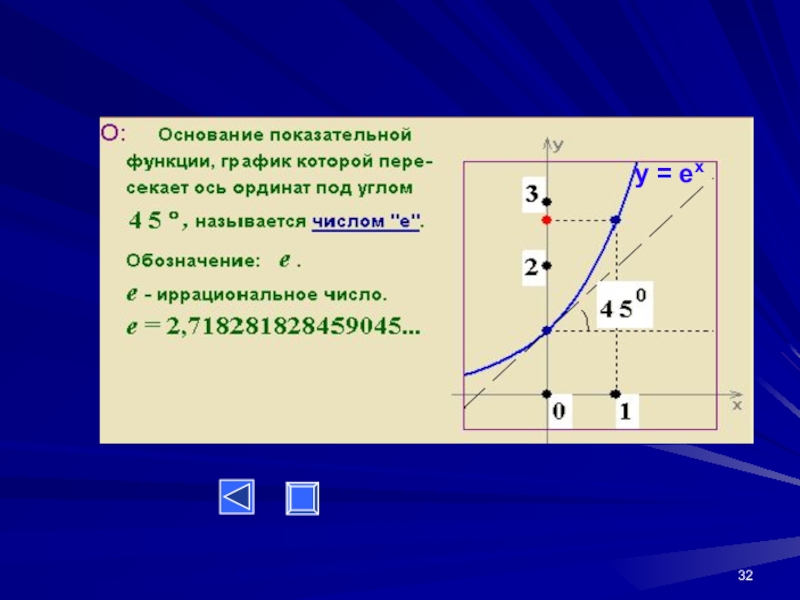
- 32. y = ex
Слайд 1Логарифмические
уравнения
Теория, примеры и решения.
Рекомендуется учащимся-старшеклассникам для самостоятельной подготовки к уроку,
Слайд 2 Определение логарифма
Об истории развития логарифмов
Основные
(Формулы преобразования логарифмов)
О монотонности логарифмической функции
Логарифмические уравнения
Методы решения логарифмических уравнений
Этапы решения логарифмических уравнений
Проверь себя
Готовься к ЕГЭ
Слайд 4Определение и свойства
логарифма
(смотри урок-фильм)
Для продолжения урока-фильма Меню - Control –
Слайд 5Об истории развития логарифмов
Слово логарифм происходит от слияния греческих слов
Первые таблицы десятичных логарифмов были составлены в 1617 г. английским математиком Бриггсом. Многие из них были выведены с помощью выведенной Бриггсом формулы.
Изобретатели логарифмов не ограничились созданием логарифмических таблиц, уже через 9 лет после их разработки в 1623 г. Английским математиком Гантером была создана первая логарифмическая линейка. Она стала рабочим инструментом для многих поколений. В настоящее время мы можем находить значения логарифмов, используя компьютер. Так, в языке программирования BASIC с помощью встроенной функции можно находить натуральные логарифмы чисел.
Слайд 8Гимназия № 8, г. Сочи
Чернобабова К.В.
Первые таблицы логарифмов назывались
«Описание удивительной
(1614 г.) и
«Устройство удивительной таблицы логарифмов»
(1619 г.)
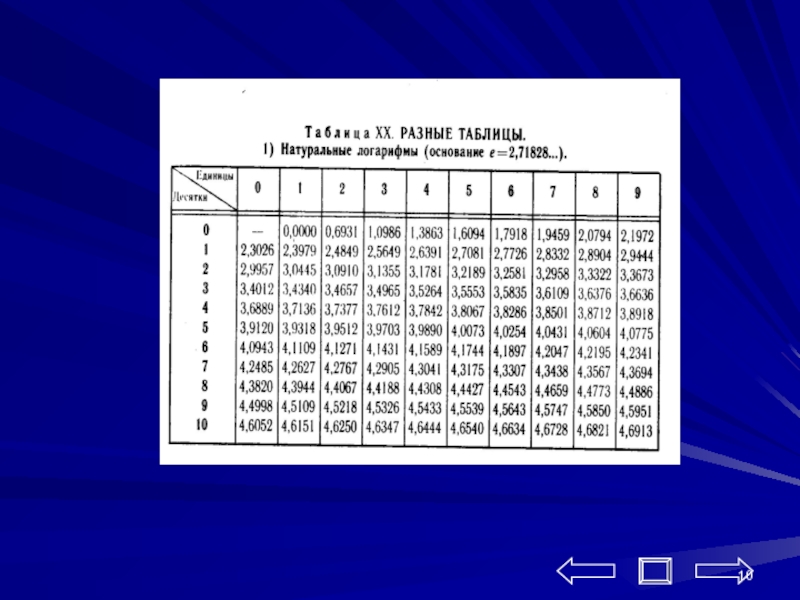
Слайд 12 Логарифм можно найти теперь с помощью ПК LOG(x) -
1) x = LOG(2.7)
PRINT x
Ответ: .993124…
2) x = LOG(1)
PRINT x
Ответ: 0
3) x %= LOG(2.7)
PRINT x
Ответ: 1
Слайд 16Если f(x)>0 и g(x)>0, a>0 и a ≠ 1, то
равносильно уравнению
f(x)=g(x)
Теорема о корне
Пусть функция f(x) возрастает (или убывает) на промежутке Х, число a – любое значение функции на этом промежутке. Тогда уравнение f(x)=a имеет единственный корень в промежутке Х.
Решая уравнение, следует помнить также теорему о корне
Слайд 18Методы решения логарифмических уравнений:
1. Потенцирование
Пример 1 Пример 2 Пример
2. Введение новой переменной
Пример 1
3. Переход к новому основанию
Пример 1
4. Разные методы решения
Пример 1 Пример 2
Для продолжения решения: Меню - Control - Play
Для продолжения решения: Меню - Control - Play
Для продолжения решения: Меню - Control - Play
Для продолжения решения: Меню - Control - Play
Слайд 19Гимназия № 8, г. Сочи
Чернобабова К.В.
Этапы решения уравнения
Найти область допустимых
Решить уравнение, выбрав метод решения
Проверить найденные корни непосредственной подстановкой в исходное уравнение или выяснить, удовлетворяют ли они условиям ОДЗ
Посмотри еще один подход к решению логарифмического уравнения
Слайд 22Гимназия № 8, г. Сочи
Чернобабова К.В.
1) Сравни с 1 log10991098
2)
меньше 1
больше 1
3) Графики уравнений отличаются или совпадают?
Ответ:
отличаются
В ОДЗ 1-го уравнения не входит точка х=0, (точка «выколота»).
Ответы (щелкни)
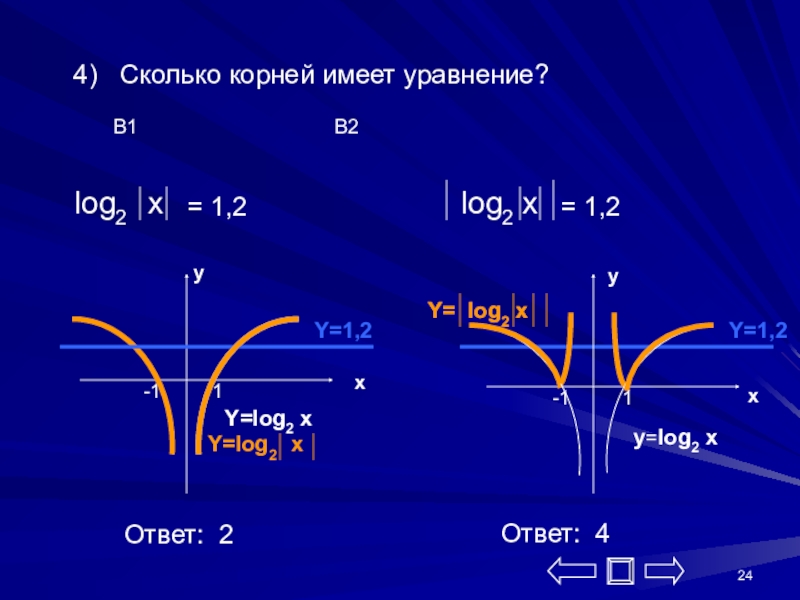
Слайд 244) Сколько корней имеет уравнение?
В1
= 1,2
1
-1
Y=1,2
Y=log2 x
y
x
y=log2 x
Y=1,2
Y=log2 x
-1
1
Ответ: 2
Ответ: 4
Слайд 26Формулы преобразования логарифмов
и их использование при решении задач
Примеры
Примеры 2
Для продолжения фильма: Ctrl + Enter
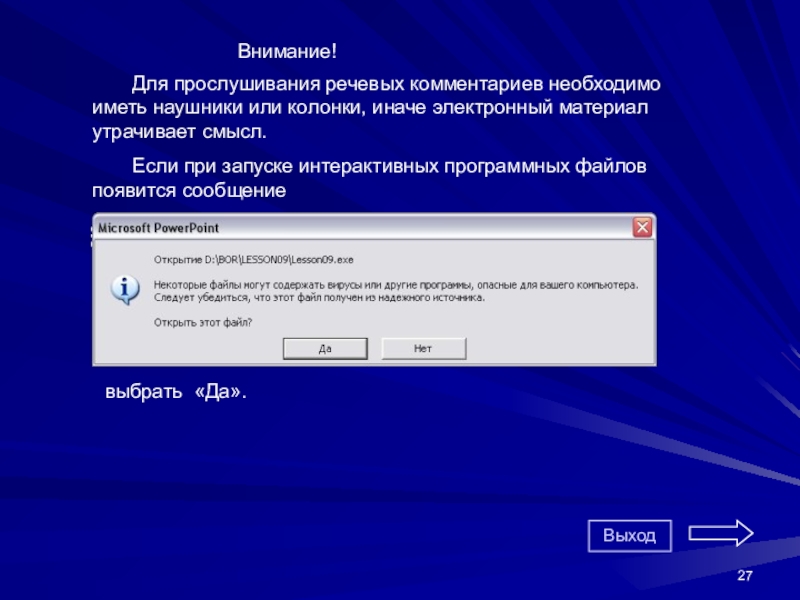
Слайд 27 Для прослушивания речевых комментариев необходимо иметь наушники или колонки, иначе электронный
Если при запуске интерактивных программных файлов появится сообщение
Выход
выбрать «Да».
Внимание!
Слайд 28
Существует несколько методических подходов к решению логарифмических уравнений. Особенно
Автор учебника «Алгебра и начала анализа 10-11» А.Г. Мордкович сравнивает разные подходы к решению:
«... Второй подход заключается в следующем: не находят ОДЗ, а сразу решают уравнение f (х) = g (x). Затем все найденные корни проверяют непосредственной их подстановкой в исходное уравнение.
Чем плох первый подход? Тем, что иногда решение системы неравенств, определяющей ОДЗ уравнения, бывает весьма затруднительным, отвлекающим от основной работы — от решения уравнения. При этом часто бывает так, что уравнение f (x) = g (x) вообще не имеет корней, так что вся работа по опережающему отысканию ОДЗ оказывается пустой тратой времени.
Бывает и так, что указанное уравнение имеет настолько простые корни, что их проверка подстановкой в исходное уравнение осуществляется легко и быстро. В таких случаях предпочтительнее второй подход.
Далее
Слайд 29 А чем плох второй подход?
Хотя второй подход предпочтительнее по идейным соображениям. В принципе сначала нужно решить уравнение, затем сделать проверку. А при первом подходе, еще ничего не сделав для собственно решения уравнения, мы начинаем "подстилать соломку", находить ОДЗ, думая о возможном появлении посторонних корней и о необходимости их отсева.
Мы отдаем предпочтение третьему подходу, который, на наш взгляд, нивелирует недостатки, как первого, так и второго подходов.
План решения уравнения loga f (х) = loga g (x) заключается в следующем:
решаем уравнение f (х) = g (x); если уравнение имеет корни, то делаем проверку. Для этого составляем систему неравенств:
но не решаем ее, а проверяем найденные корни уравнения подстановкой в неравенства системы (что значительно проще).
Но, вообще говоря, тактика решения логарифмического уравнения может быть достаточно гибкой: если ОДЗ можно найти без труда, выбирайте первый подход; если с ОДЗ много возни, то выбирайте третий подход (или второй — в случае очень простых корней).»
Далее
Слайд 30
Еще раз о третьем подходе к решению логарифмических
(«Готовимся к ЕГЭ» В.Н. Студенецкая)
Слайд 31
НЕПЕР Джон (1550-1617), шотландский математик, изобретатель логарифмов.
Потомок старинного воинственного шотландского рода. Изучал логику, теологию, право, физику, математику, этику. Увлекался алхимией и астрологией. Изобрел несколько полезных сельскохозяйственных орудий. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд "Описание удивительных таблиц логарифмов" опубликовал лишь в 1614 году. В конце 1620-х годов была изобретена логарифмическая линейка, счетный инструмент, использующий таблицы Непера для упрощения вычислений. С помощью логарифмической линейки операции над числами заменяются операциями над логарифмами этих чисел.
www.km.ru