- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Экономические задачи в ЕГЭ
Содержание
- 1. Экономические задачи в ЕГЭ
- 2. Виды задач экономического содержанияБанки, вклады, кредитыЗадачи на оптимальный выбор
- 3. Слайд 3
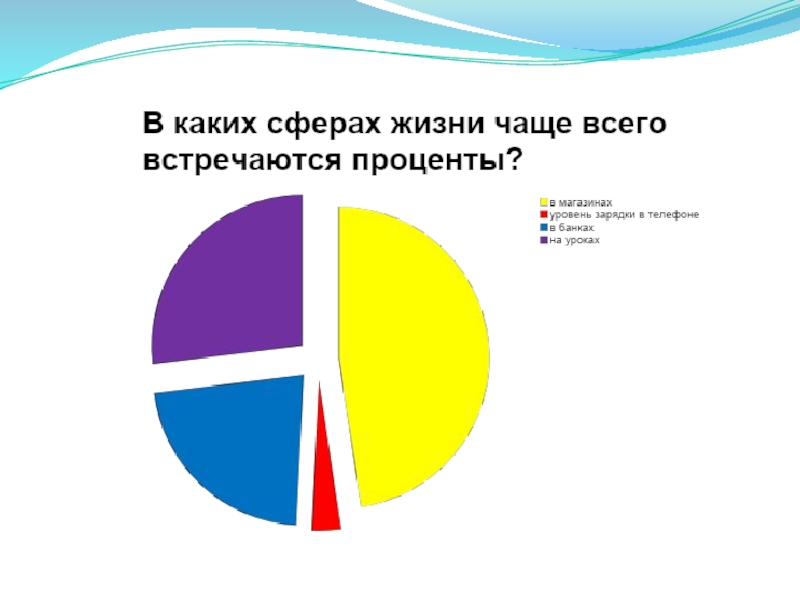
- 4. Понятие процентаПроцент- происходит от латинского «pro centum», что означает «за сотню» или «со ста».
- 5. Формула увеличения числа на заданный процент :А2
- 6. Пример 1.Банковский кредит 10 000 рублей под
- 7. Простые процентыПростые проценты — это метод расчета процентов,
- 8. Сложные процентыСложные проценты — это такой вариант,
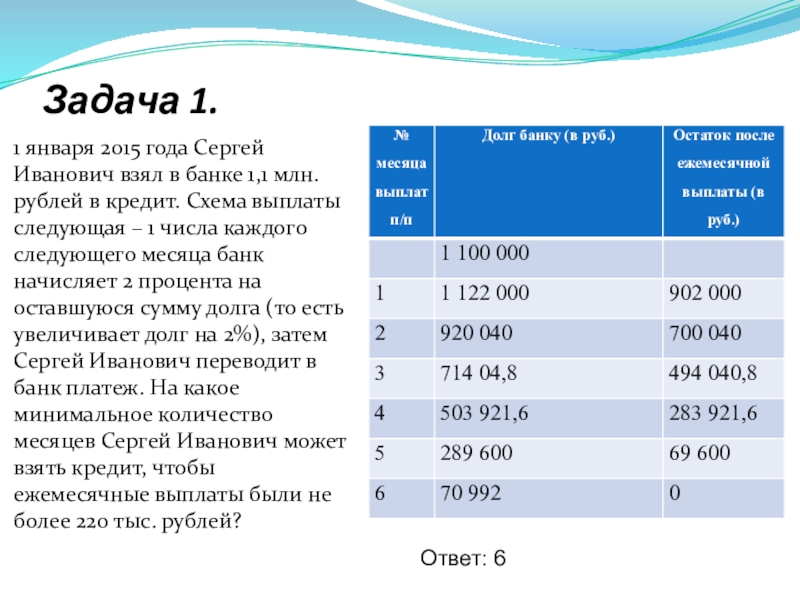
- 9. Задача 1.1 января 2015 года Сергей Иванович
- 10. Задача 2. 31 декабря 2014 года Дмитрий
- 11. Решение.Х рублей – ежегодная плата.I год: II
- 12. 31 декабря 2014 года Сергей взял
- 13. Решение.I год: II год: =III год: После
- 14. 31 декабря 2014 года Алексей взял в
- 15. Решение.S-сумма кредита,р=, где a - процентная ставка,х – сумма ежегодных выплат;, гдеОтвет: 2 296 350
- 16. 31 декабря 2014 года Родион взял в
- 17. Решение.S-сумма кредита,
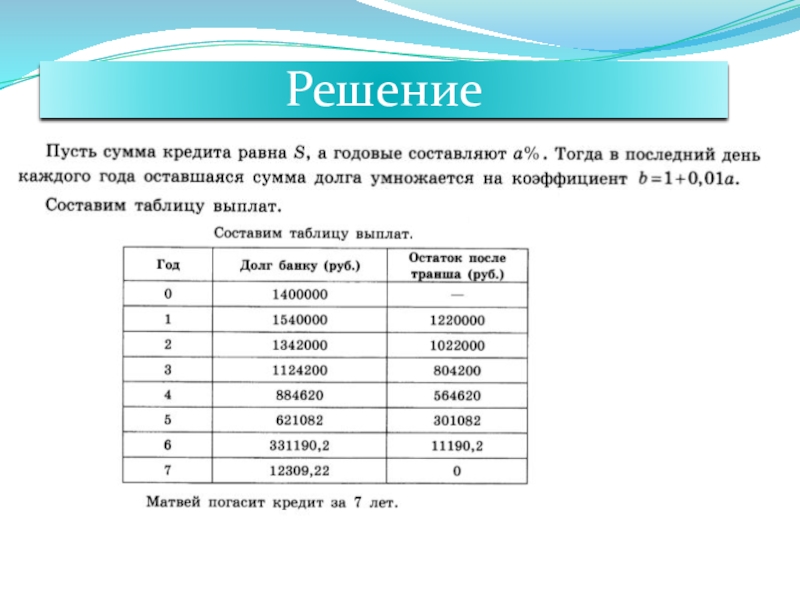
- 18. Матвей хочет взять в кредит 1,4 млн.
- 19. Решение
- 20. Другой способ решения задачи №6Аннуитетный платеж –
- 21. Слайд 21
- 22. Использовать формулу аннуитетного платежа
- 23. Задача №7В июле планируется взять кредит в
- 24. Решение
- 25. Задача № 915-го января планируется взять кредит
- 26. Решение
- 27. Решение
- 28. Задачи на оптимальный выбор
- 29. Задача №1
- 30. Решение
- 31. Решение
- 32. Решение
- 33. Решение
- 34. Решение
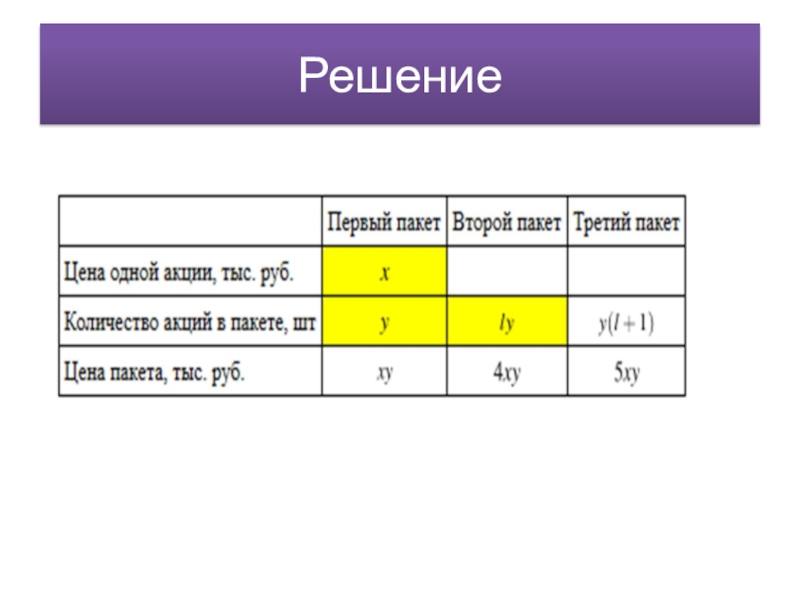
- 35. Задача №2Имеется три пакета акций. Общее суммарное
- 36. Решение
- 37. Решение
- 38. Решение
- 39. В двух
- 40. Слайд 40
- 41. Слайд 41
- 42. В отеле могут быть стандартные номера площадью
- 43. Слайд 43
- 44. У фермера есть два поля, каждое
- 45. Пусть х га на первом
Слайд 4Понятие процента
Процент- происходит от латинского «pro centum», что означает «за сотню»
Слайд 5Формула увеличения числа на
заданный процент :
А2 = А1 + А1
или
A2 = A1 * (1 + P / 100 )
Слайд 6Пример 1.
Банковский кредит 10 000 рублей под 5 процентов. Общая сумма
А2 = 10000 * ( 1 + 5 / 100 ) = =10000 * 1.05 = 10 500
Слайд 7Простые проценты
Простые проценты — это метод расчета процентов, при котором начисления происходят
Простыми процентами можно считать вклад (долг) только в том случае, если происходит однократная выплата процентов и всей суммы вклада(долга) одновременно, при этом полностью отсутствует возможность досрочной частичной или полной выплаты вклада (долга) и/или полностью отсутствует возможность пролонгации вклада(долга).
Слайд 8Сложные проценты
Сложные проценты — это такой вариант, при котором происходит капитализация
Капитализация происходит не постоянно, а с некоторой периодичностью. Как правило, периоды равны месяцу, кварталу или году.
Слайд 9Задача 1.
1 января 2015 года Сергей Иванович взял в банке 1,1
Ответ: 6
Слайд 10Задача 2.
31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей
Слайд 11Решение.
Х рублей – ежегодная плата.
I год:
II год:
После второго взноса
Ответ: 2 622 050
Слайд 12
31 декабря 2014 года Сергей взял в банке 6 944 000 рублей в
Задача 3.
Слайд 13Решение.
I год:
II год:
=
III год:
После третьего взноса кредит погашен
Ответ: 2 916 000
Слайд 1431 декабря 2014 года Алексей взял в банке 6 902 000 рублей в
Задача 4.
Слайд 15Решение.
S-сумма кредита,
р=
, где a - процентная ставка,
х – сумма ежегодных выплат;
,
Ответ: 2 296 350
Слайд 1631 декабря 2014 года Родион взял в банке некоторую сумму в
Задача 5.
Слайд 17Решение.
S-сумма кредита,
,где a
суммы ежегодных выплат:
1 464 100 обозначим в (на четыре года),
2 674 100 обозначим с (на два года).
В общем виде рассчитаем оплату кредита
за два года и за четыре года.
I. За два года:
II. За четыре года:
В полученное выражение подставим числовые значения.
Ответ: 10
Слайд 18Матвей хочет взять в кредит 1,4 млн. рублей. Погашение кредита происходит
Задача 6.
Слайд 20Другой способ решения задачи №6
Аннуитетный платеж – вариант ежемесячного платежа по
Слайд 23Задача №7
В июле планируется взять кредит в банке на сумму 28
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Слайд 25Задача № 9
15-го января планируется взять кредит в банке на 39
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Слайд 35Задача №2
Имеется три пакета акций. Общее суммарное количество акций первых двух
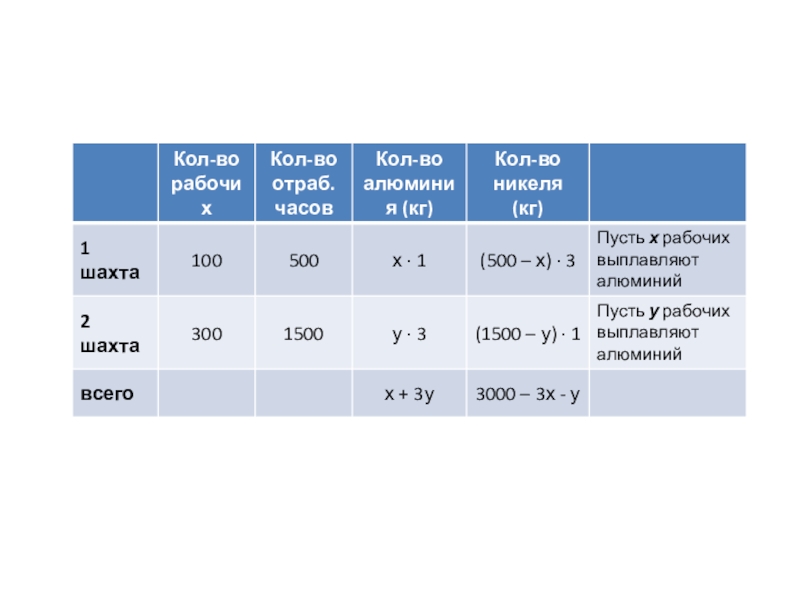
Слайд 39 В двух шахтах добывают алюминий и
Задача № 3
Слайд 42В отеле могут быть стандартные номера площадью 21 кв м и
Задача № 4
Слайд 44 У фермера есть два поля, каждое площадью 10 гектаров. На
Задача № 5