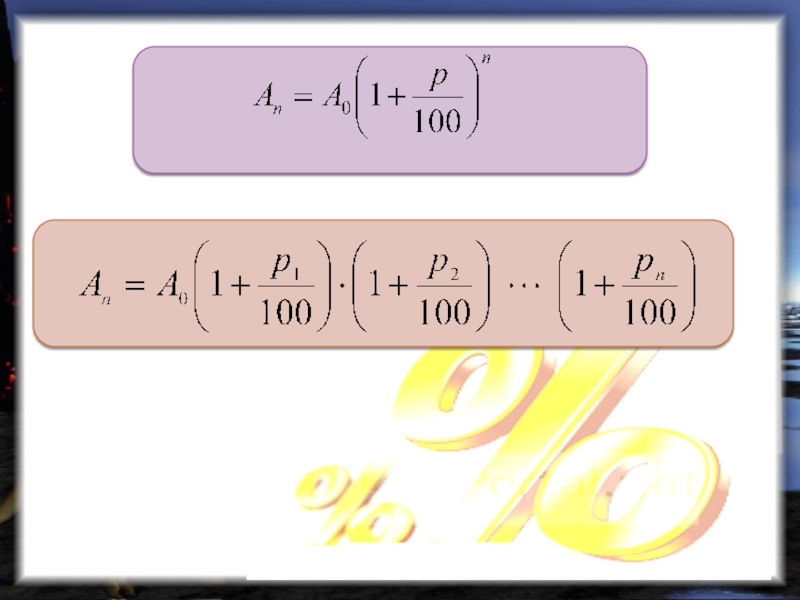Презентация, доклад на тему Экономические задачи

городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе первого города трудятся суммарно часов в неделю, то за эту неделю они производят 2t единиц товара, а рабочие на заводе второго города, если трудятся суммарно часов в неделю, то за эту неделю они производят 5t единиц товара. На обоих заводах за каждый час работы Петя платит рабочему 500 руб. Какую наименьшую сумму придется тратить на оплату рабочим в неделю, чтобы производилось 580 единиц товара в неделю?  

городе суммарно трудятся одинаково. Пусть в первом городе рабочие суммарно трудятся х2 часов, а рабочие на заводе второго города у2 часов. Тогда за х2 часов рабочие произведут 2х единиц товара, а рабочие второго города за у2 часов рабочие произведут 5у единиц товара. По условию

Задача свелась к нахождению наименьшего значения функции S(х) на
промежутке

Найдем критические точки

=0 при х = 40.

Ответ. 5 800 000.

в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе первого города трудятся суммарно t2 часов в неделю, то за эту неделю они производят 2t единиц товара, а рабочие на заводе второго города, если трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. На обоих заводах за каждый час работы Григорий платит рабочему 500 руб. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах, если Григорий готов заплатить 5000000 рублей в неделю на оплату труда рабочих?

суммарно трудятся одинаково. Пусть в первом городе рабочие суммарно трудятся х2 часов, а рабочие на заводе второго города у2 часов.

а количество единиц товара, которое можно произвести за неделю на этих двух заводах, равно

.

Находим наибольшее значение функции на отрезке

[0; 100].

Ответ.500.

Тогда за х2 часов рабочие произведут 2х единиц товара, а рабочие второго города произведут 5у единиц товара. По условию

сколько процентов повысилась зарплата в первый раз, если второе повышение было вдвое больше первого?

Решение. Пусть в первый раз зарплата повысилась на х %.

Ответ. 25%

число процентов, а затем трижды уменьшали на то же число процентов. В результате получили число 21,6. На сколько процентов увеличивали число?

Решение. Если обозначить через х – искомое количество процентов,
то по формуле (2) получим:

Ответ. На 50%.

р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции?

Решение. Пусть первый брокер купил акции на а рублей, а второй – на (3640 – а) рублей, а цена на акции возросла на у %. Тогда у брокеров стало, соответственно, а(1+0, 01у) р. и (3640 – а) (1+0, 01у) р. денег.

Ответ. Цена одной акции возросла на 37,5 %.

рублей в кредит на 4 года под 20% годовых, чтобы купить своей жене Рите новую шубу. Схема выплаты кредита следующая: утром 8 марта следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), а вечером того же дня Леня переводит в банк определенную сумму ежегодного платежа (все четыре года эта сумма одинакова). Какую сумму сверх взятых 53 680 рублей должен будет выплатить банку Леня Голубков за эти четыре года?

рублей.

Вечером 8 марта через год Леня переводит в банк определенную сумму ежегодного платежа, которую обозначим Х.

Тогда у него останется долг

Через два года долг станет равным

.

Вечером Лена отдает очередную сумму и у него остается долг

Через три года:

,

После отдачи:

На четвертый год:

а за 4 года – 82944 рубля, следовательно, сверх взятых 53680 рублей
Леня должен был выплатить 82944-53680=29264 рубля.
Ответ. 29264.

него средств клиентов в акции золотодобывающего комбината, а остальные 70% – в строительство торгового комплекса.
В зависимости от обстоятельств первый проект может принести банку прибыль в размере от 32% до 37% годовых, а второй проект – от 22% до 27% годовых.
В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке, уровень которой должен находиться в пределах от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в покупку акций и строительство торгового комплекса может при этом получить банк.

когда он получит максимальную прибыль (по первому проекту 37% , по второму - 27%) и выплатить клиентам минимальные проценты по установленной ставке (10%).

Пусть банк располагает средствами в размере х руб.
Тогда 0,7 средств, вложенных во второй проект, могут принести прибыль в сумме от 1,22∙0,7х =0,854 х  до 1,27∙0,7х =0,889х  рублей, а 0,3х  средств, вложенных в акции золотодобывающего комбината, могут принести прибыль в сумме от 1,32∙0,3х =0,396 х до 1,37∙0,3х =0,411 х рублей.

Наименьшую же прибыль получит банк в том случае, когда он получит минимальную прибыль (по первому проекту 32% , по второму - 22%) и выплатить клиентам максимальные проценты по установленной ставке (20%).

по заранее установленной ставке от 1,1х до 1,2 х.
Тогда по сказанному выше, наименьшая прибыль равна
0,854 х +0,396 х - 1,2 х =0,05х, т.е. 5%,
наибольшая прибыль равна
0,889х +0,411 х – 1,1х = 0,2х, т.е. 20%
Ответ. 5% и 20%.

1 млн рублей в кредит.
Схема выплаты такая - 31 декабря следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на %), затем Георгий Исаевич переводит очередной транш.
Георгий Исаевич выплатил кредит за два транша, переводя в первый раз 570 тыс. рублей, во второй 599,4 тыс. рублей. Под  какой процент банк выдал кредит Георгию Исаевичу?

года Георгий Исаевич будет должен банку

После выплаты 570 тыс. руб. у него останется долг
где
а второй год долг составит

Если из этой суммы вычесть 599,4 тыс. рублей (второй транш), то Георгий Исаевич рассчитается с банком полностью, т.е. получим уравнение:

Следовательно, m=1,11 где

Ответ:11%

1,1 млн рублей в кредит.
Схема выплаты кредита следующая - 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж.
На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей?

млн рублей, если будет платить не по 275 тыс. рублей. Таким образом, он не покроет долг с процентами.
  Каждый месяц долг увеличивается не более, чем на
1100000 · 0,01 = =11000 рублей.  
Значит, за пять месяцев Александр Сергеевич должен будет выплатить не более
1100000 + 5 · 11000 = 1155000 рублей,  
что менее, чем
5 · 275000 = 1375000 рублей.
  Таким образом, Александр Сергеевич сможет выплатить кредит за 5 месяцев.
   Ответ. 5.

уже решили, за кого из двух кандидатов они будут голосовать. При этом 55% из них решили голосовать за кандидата А. Какой процент из тех, кто еще не определил своего избранника, должен голосовать за кандидата А, чтобы за него проголосовала по крайней мере половина избирателей?

Решение. Пусть избирателей – х  человек.
Тогда 0,6x уже решили, за кого из двух кандидатов они будут голосовать. При этом  0,55∙0,6x  голосуют за кандидата А.
Не определили своего избранника – 0,4x человек.
Чтобы за кандидата А проголосовала по крайней мере половина избирателей (то есть x/2), необходимо, чтобы из еще не определивших своего избранника, за кандидата А проголосовало x/2 - 0,55∙0,6x  человек.
Итак, поскольку x/2 - 0,55∙0,6x =0,17x, то процент из тех, кто еще не определил своего избранника, но должен голосовать за кандидата А, составляет %).
Ответ. 42,5.

20% из которых были фальшивыми. Некая криминальная структура стала ввозить в страну по 100 000 долларов в месяц, 10% из которых были фальшивыми. В это же время другая структура стала вывозить из страны 50 000 долларов ежемесячно, из которых 30% оказывались фальшивыми. Через сколько месяцев содержание фальшивых долларов в стране составит 5%?

и 800000 настоящих долларов и некая криминальная структура стала ввозить в страну в месяц 10000 фальшивых долларов и 90000 настоящих.
С учетом ввоза 1-й месяц настоящих долларов станет – 100000+90000=890000, а фальшивых долларов – 200000+10000=210000.
В тоже время из страны вывозится  15000 фальшивых долларов и 35000 настоящих каждый месяц.
Тогда с учетом ввоза и вывоза за 1-й месяц в стране окажется 890000-35000=855000 настоящих долларов и 210000-15000=195000 фальшивых долларов,
то есть за месяц в итоге  в стране появляется дополнительно 55000 настоящих долларов, а количество фальшивых уменьшается на 5000 долларов.

200000- 5000 n фальшивых долларов, а всего 1000000+50000 n долларов.
Содержание фальшивых долларов в стране  через n  месяцев составит 5%, если 200000- 5000 n =0,05(1000000+50000 n ), откуда n =20
Ответ. 20.

свеча была зажжена на час раньше двух других, зажженных одновременно. В некоторый момент горения первая и третья свечи стали одинаковой длины, а через 2 часа после этого одинаковой длины стали третья и вторая свечи. За сколько часов сгорает третья свеча, если вторая сгорает за 6 ч, а первая –за 4 ч?

условию имеем:

начала горения III–ей свечи.

часа после того, как стали  одинаковой длины  первая и третья свечи (заметим, первая и вторая свечи зажжены были одновременно), теперь уже стали одинаковой длины  третья и вторая свечи, то

 Итак, учитывая (1) и (2), имеем:

. Ответ. 8.