- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Числовая окружность на координатной прямой. 10 класс, учебник Мордкович.
Содержание
- 1. Числовая окружность на координатной прямой. 10 класс, учебник Мордкович.
- 2. Определение.Числовая окружность на координатной плоскости.Расположим числовую окружность
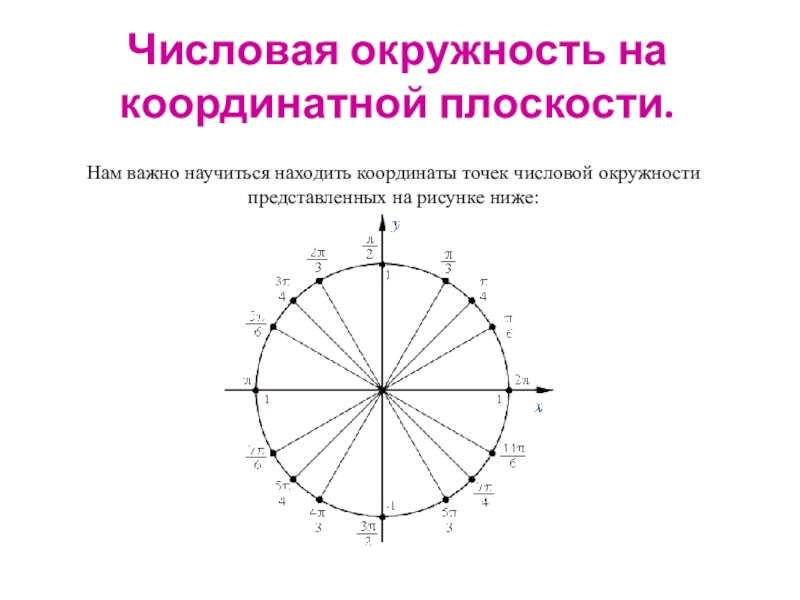
- 3. Числовая окружность на координатной плоскости.Нам важно научиться находить координаты точек числовой окружности представленных на рисунке ниже:
- 4. Числовая окружность на координатной плоскости.Найдем координату точки
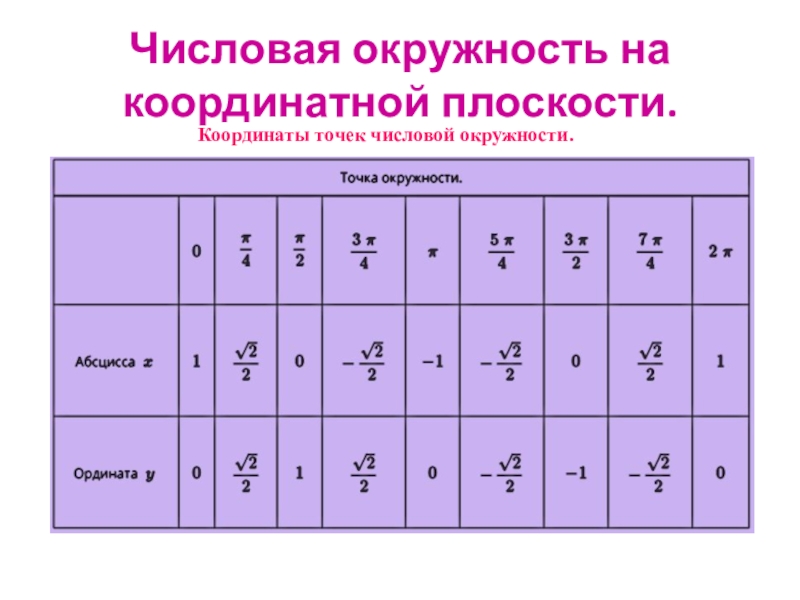
- 5. Координаты точек числовой окружности.Числовая окружность на координатной плоскости.
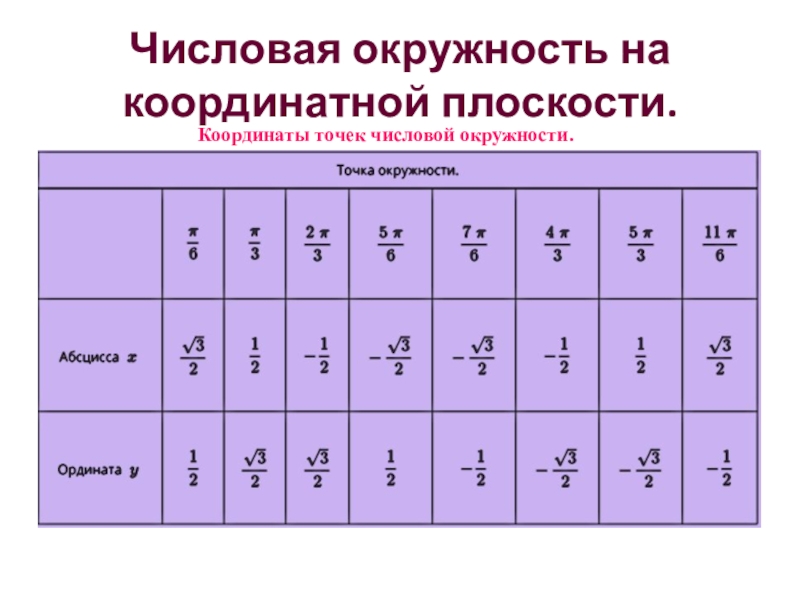
- 6. Координаты точек числовой окружности.Числовая окружность на координатной плоскости.
Слайд 1Алгебра и начала математического анализа, 10 класс.
Урок на тему:
Числовая окружность на
Слайд 2Определение.
Числовая окружность на координатной плоскости.
Расположим числовую окружность в координатной плоскости так,
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
x > 0, у > 0 в первой четверти;
х < 0, у > 0 во второй четверти;
х < 0, у < 0 в третьей четверти;
х > 0, у < 0 в четвертой четверти.
Для любой точки М(х; у) числовой окружности выполняются неравенства -1 < x < 1; -1 < у < 1.
Запомните!
уравнение числовой окружности:
Слайд 3Числовая окружность на координатной плоскости.
Нам важно научиться находить координаты точек числовой
Слайд 4Числовая окружность на координатной плоскости.
Найдем координату точки π/4:
Точка М(π/4) —
Значит, треугольник OMP - равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x = y
Так как координаты точки M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
Решив данную систему получаем:
Получили, что координаты точки M, соответствующей числу π/4 будут
Аналогичным образом рассчитываются координаты точек представленных на предыдущем слайде.