- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Барицентрический метод (10-11 класс)
Содержание
- 1. Барицентрический метод (10-11 класс)
- 2. Мудрость прошлого
- 3. Актуальность проекта Барицентрический
- 4. Цель Рассмотреть барицентрический
- 5. Задачи:ознакомиться с историей открытия барицентрического метода; рассмотреть
- 6. Теоретический этапИсторический этапИсследовательская деятельностьЭтапы работы над проектом
- 7. Слайд 7
- 8. Данный метод был использован и
- 9. Применение свойств В строительстве: 1)
- 10. Слайд 10
- 11. Исследовательская деятельность
- 12. Цель Структурировать и классифицировать задачи, решаемые данным
- 13. А где же геометрия?
- 14. Центр масс A Bm1m2! m2 >
- 15. Треугольник и теорема о перераспределении масс
- 16. 2) принадлеж - ность центра масс двух
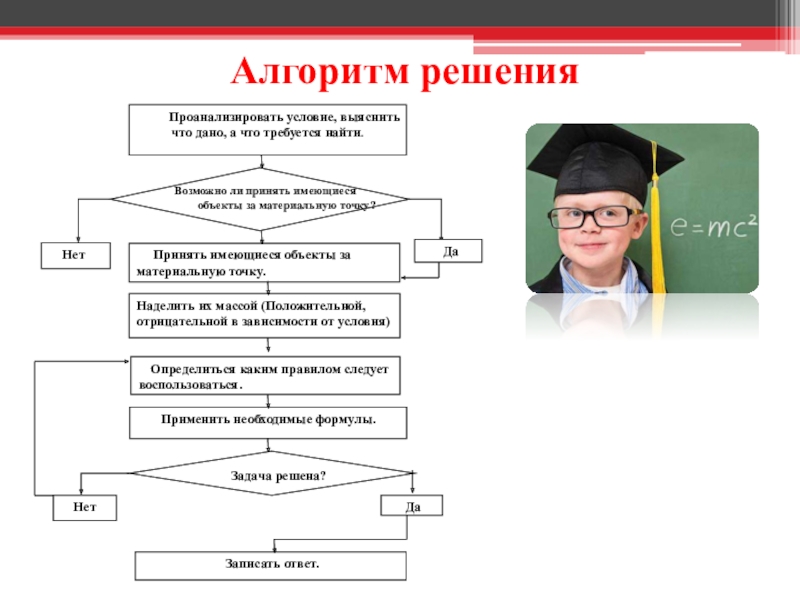
- 17. Алгоритм решенияВозможно ли принять имеющиеся объекты за материальную точку?Задача решена?
- 18. Доверяй, но проверяй!Решение задач естественно научного циклаРешение химических задачРешение математиче-ских задач
- 19. Слайд 19
- 20. Теорема о трех медианах
- 21. Планиметрическая задача, С4В117(13)(17) Дан прямоугольный треугольник АВС
- 22. Стереометрическая задача2) Т.к
- 23. Неравенство Коши - Буняковского
- 24. Химическая задача
- 25. Слайд 25
- 26. Заключение В результате данной
- 27. СПАСИБО ЗА ВНИМАНИЕ!!!
Слайд 1«Барицентрический метод.
Геометрия, которую я люблю»
Выполнила:
Ученица 10А класса
Багаева Наталия
Научный руководитель:
Красина
Слайд 2Мудрость прошлого
«...Я счел
Архимед
Слайд 3Актуальность проекта
Барицентрический метод позволяет более рационально
Благодаря данному методу у учащихся формируется так называемое нестандартное мышление, способствующие пониманию природы происходящих событий.
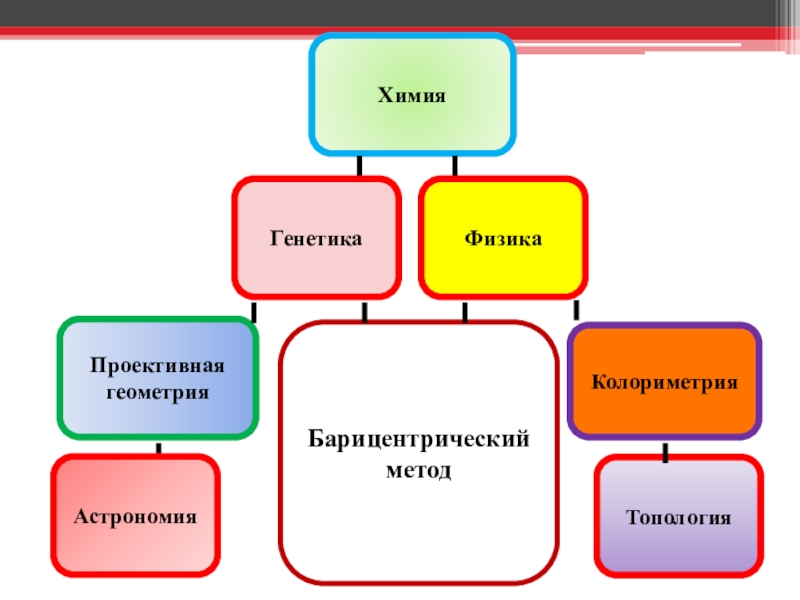
Выбранная мной тема тесно связана с топологией. В свою очередь топология считается на данный момент самым актуальным и перспективным разделом высшей математики
Слайд 4Цель
Рассмотреть барицентрический метод и возможность его
Слайд 5Задачи:
ознакомиться с историей открытия барицентрического метода;
рассмотреть основные формулировки, свойства,
изучить центроиды треугольника и тетраэдра;
провести исследовательскую деятельность, направленную на определение области применения барицентрического метода;
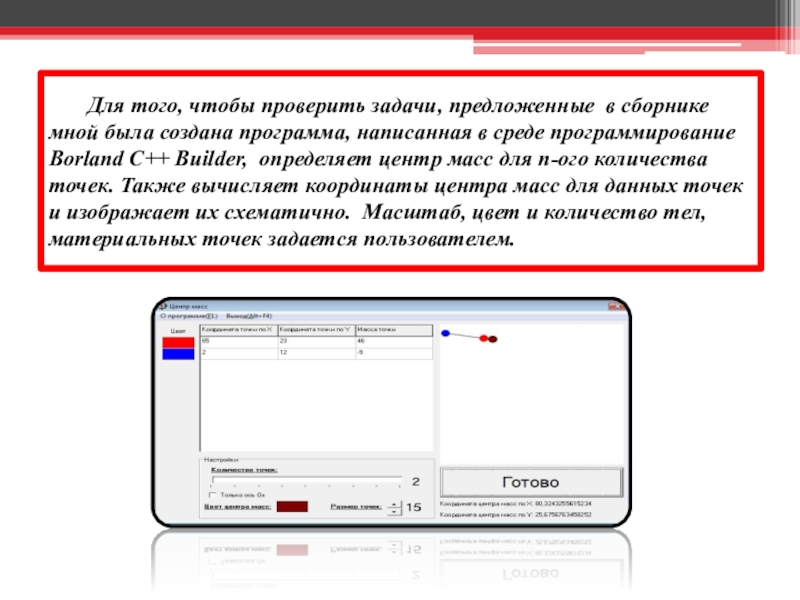
создать программу в среде Borland C++ Builder, с целью проверки задач.
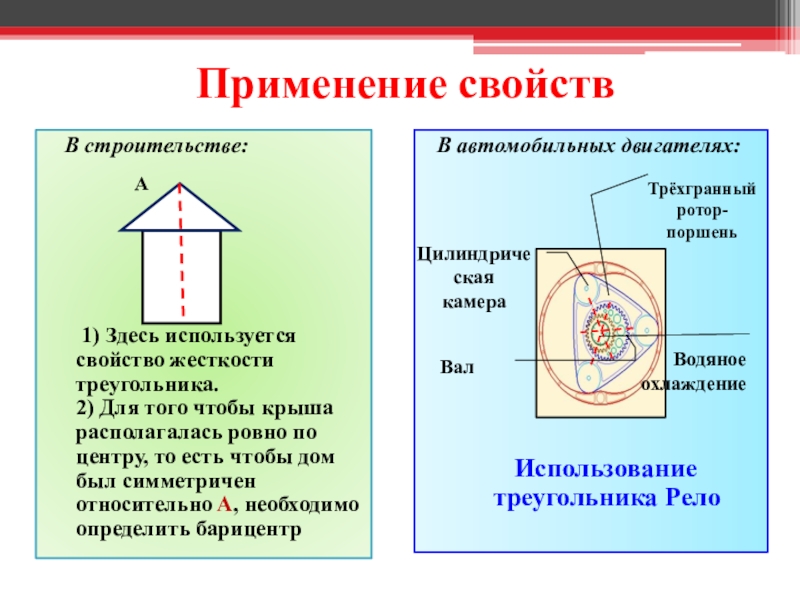
Слайд 9Применение свойств
В строительстве:
1) Здесь используется свойство жесткости
В автомобильных двигателях:
Использование треугольника Рело
Трёхгранный ротор-поршень
Водяное охлаждение
Вал
Цилиндрическая камера
Слайд 12Цель
Структурировать и классифицировать задачи, решаемые данным методом.
Создать тематический сборник.
Создать
Исследовать область практического применения барицентрического метода
Задачи
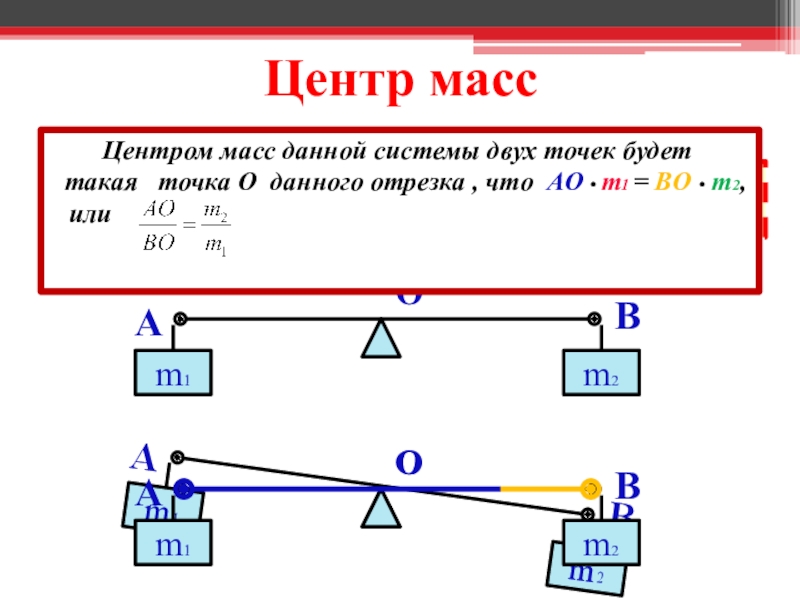
Слайд 14Центр масс
A
B
m1
m2
! m2 > m1
O
Центром масс данной системы двух точек будет такая точка O данного отрезка , что AO • m1 = BO • m2,
или
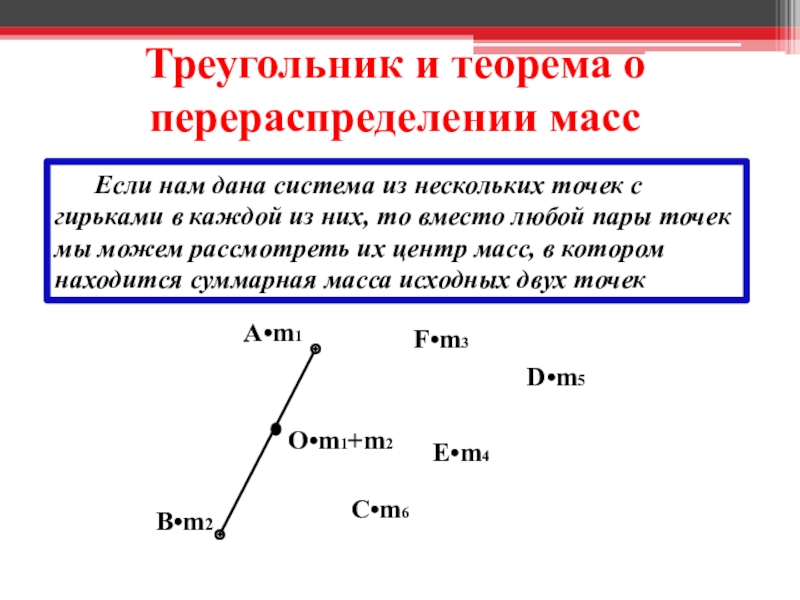
Слайд 15Треугольник и теорема о перераспределении масс
Если нам дана
A•m1
B•m2
F•m3
C•m6
D•m5
E•m4
O•m1+m2
Слайд 162) принадлеж - ность центра масс двух м. т. отрезку, соединяющему
Тонкости при решении
При решении геометрической задачи барицентрическим методом мы загружаем отдельные точки массами
Затем привлекаем свойства центров масс всех полученных м. т. или части этих м. т.
1) наличие и единственность центра масс у любой системы материальных точек;
3) возможность перегруппировки материальных точек системы без изменения положения центра масс всей системы
Искусство применения барицентрического метода состоит в том, чтобы по условию задачи осуществить такой выбор точек и помещаемых в эти точки масс, при котором задача легко и красиво решается.
Слайд 18 Доверяй, но проверяй!
Решение задач естественно научного цикла
Решение химических задач
Решение
Слайд 19
Физические задачи:
а) задачи на нахождение моментов сил;
б) задачи на нахождение рычага;
Расчетные задачи в колориметрии;
Задачи в популяционной генетике.
Решение математических задач
Задачи на нахождение отношение элементов в треугольнике и других простейших геометрических фигурах;
Задачи на нахождение объема и площади сферических тел, многогранников, их элементов и т.д;
Задачи с использованием векторных преобразований;
Задачи, сводящиеся к доказательству алгебраических неравенств;
Решение химических задач
Задачи на нахождения процентного содержания вещества в сплаве, растворе;
Задачи на нахождения массы и массовой доли;
Задачи на расчет объемных отношений газов при химических реакциях;
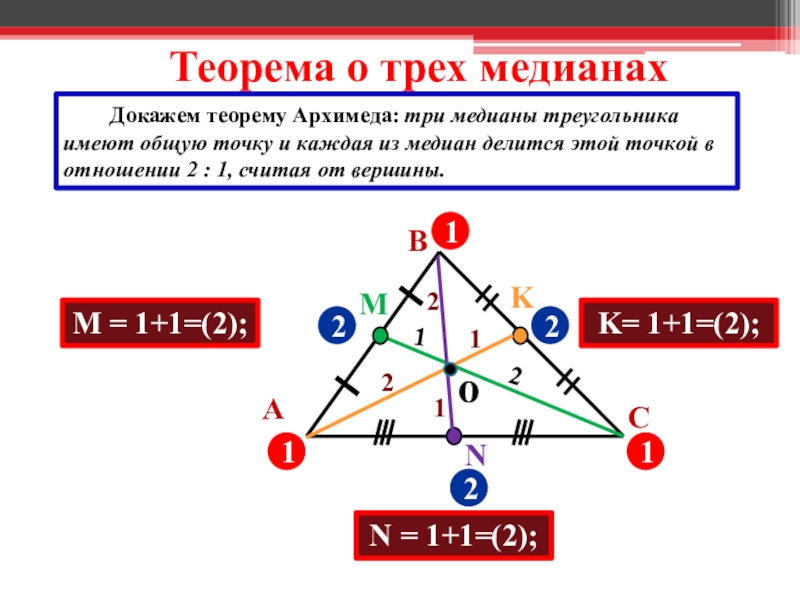
Слайд 20 Теорема о трех медианах
Докажем теорему
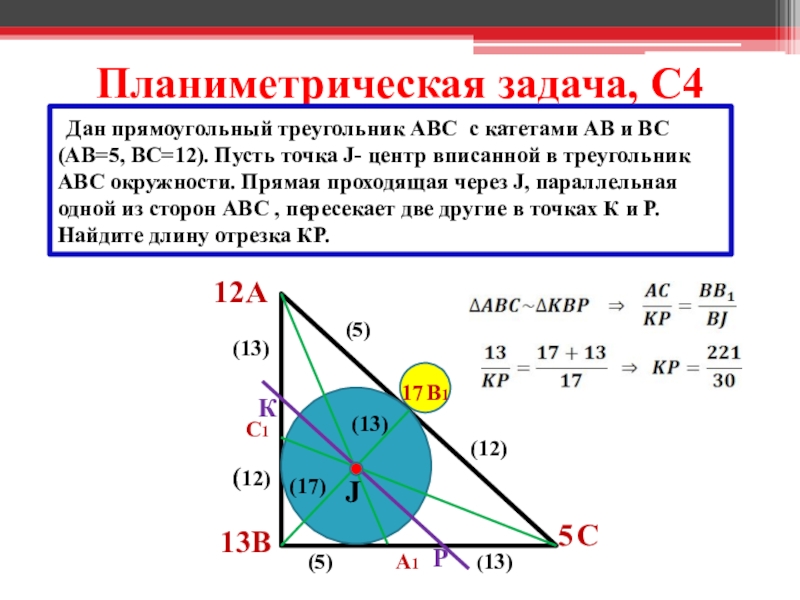
Слайд 21Планиметрическая задача, С4
В1
17
(13)
(17)
Дан прямоугольный треугольник АВС с катетами АВ и
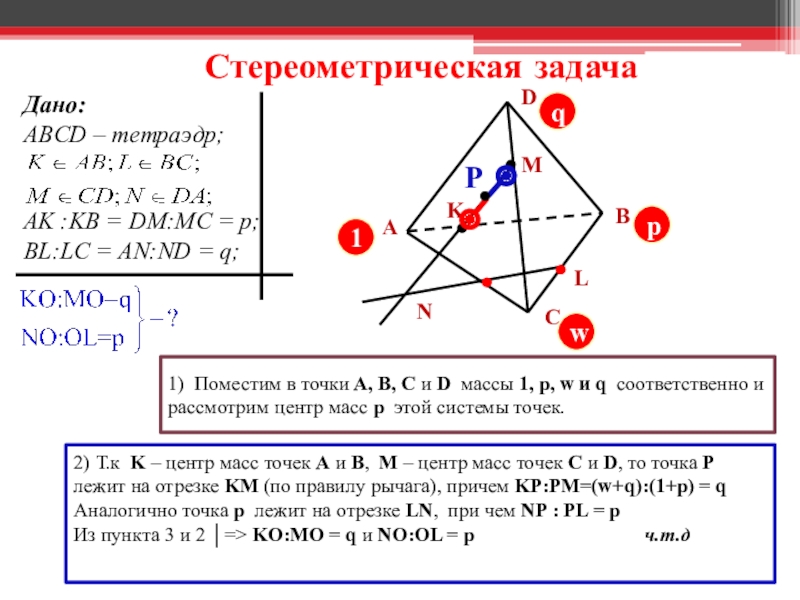
Слайд 22 Стереометрическая задача
2) Т.к K – центр масс
Аналогично точка p лежит на отрезке LN, при чем NP : PL = p
Из пункта 3 и 2 │=> KO:MO = q и NO:OL = p ч.т.д
Дано:
ABCD – тетраэдр;
AK :KB = DM:MC = p;
BL:LC = AN:ND = q;
1
p
w
q
1) Поместим в точки A, B, C и D массы 1, p, w и q соответственно и рассмотрим центр масс p этой системы точек.
Слайд 23Неравенство Коши - Буняковского
Пусть m1, …, mn
│ => (по свойству однородности)
Пусть тогда (1) истинно.
ч.т.д
A1
An
m1
m2
(1)
Слайд 25 Для того, чтобы проверить задачи,
Слайд 26Заключение
В результате данной исследовательской работы было установлено,
Данный метод является универсальным. Границы применимости охватывают широкий спектр наук;
И действительно, данный метод может быть предложен не только как дополнительный материал на факультативных занятиях в школе, но и как опорный материал при по подготовке к экзаменам в вузах