- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Ашық сабақ Виет теоремасы
Содержание
- 1. Ашық сабақ Виет теоремасы
- 2. Сабақ мақсаты: 1. Виет теоремасын
- 3. Қайталау сұрақтары:
- 4. Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін,
- 5. Бұл мысалдардан, келтірілген квадраттық
- 6. Слайд 6
- 7. Бұл теореманы бірінші дәлелдеген француз математигі Француа
- 8. Виет теоремасы және оған
- 9. №257
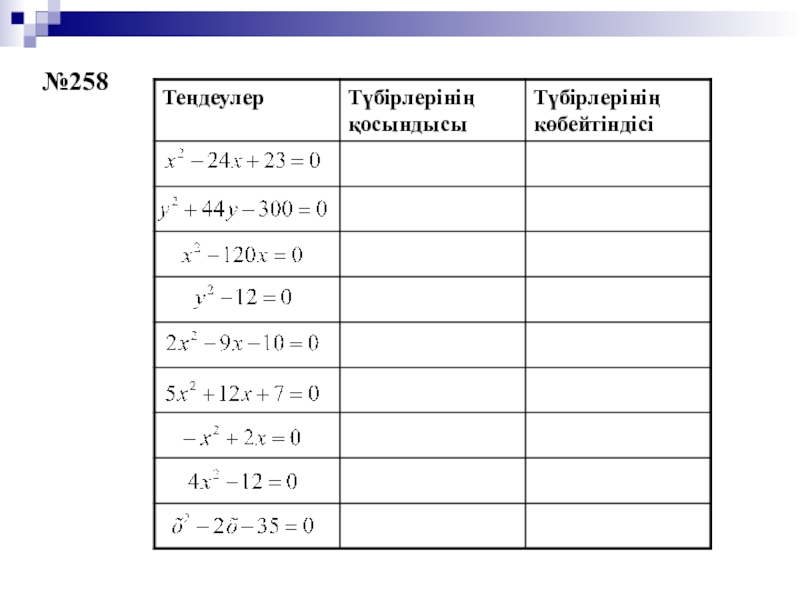
- 10. №258
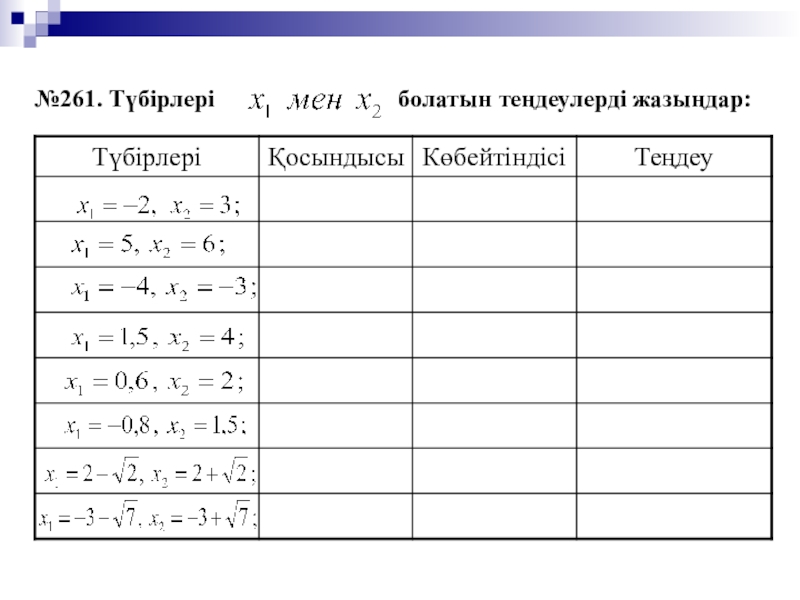
- 11. №261. Түбірлері
- 12. х2 - 12х + с = 0
- 13. Тест сұрақтары:Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін
- 14. Слайд 14
- 15. Теңдеулердің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
- 16. Үйге тапсырма: §3. №259, №260 79 бет
Сабақ мақсаты: 1. Виет теоремасын тұжырымдау және дәлелдеу. Квадрат теңдеулерді түбірлердің қасиеттерін қолдану арқылы шешуді үйрету; 2. Оқушыларға Виет теоремасын қолдану тәсілдерімен таныстыру және квадрат теңдеулерді шешуді үйрету; 3. Виет теоремасын қолдана
Слайд 2Сабақ мақсаты: 1. Виет теоремасын тұжырымдау және дәлелдеу. Квадрат теңдеулерді түбірлердің
қасиеттерін қолдану арқылы шешуді үйрету;
2. Оқушыларға Виет теоремасын қолдану тәсілдерімен таныстыру және квадрат теңдеулерді шешуді үйрету;
3. Виет теоремасын қолдана отырып есептер шығаруға оқушыларды баулу және дағдыландыру.
Слайд 3Қайталау сұрақтары:
түріндегі теңдеу қалай аталады?
формуласымен есептелетін сан қалай аталады?
3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі болады?
4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі болады?
5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады?
6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық теңдеу деп атайды?
7. теңдеуінің коэффициенттерін атап шығыңдар.
8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды?
формуласымен есептелетін сан қалай аталады?
3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі болады?
4. Егер D=0 болса, онда квадраттық теңдеудің неше түбірі болады?
5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады?
6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық теңдеу деп атайды?
7. теңдеуінің коэффициенттерін атап шығыңдар.
8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды?
Слайд 4Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің
мәндерін табыңдар және жауаптарын кестеге толтырыңдар.
Слайд 5 Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы
таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап шығайық.
Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады:
Енді бұл қасиетті теорема ретінде тұжырымдап шығайық.
Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады:
Слайд 6
(келтірілген квадрат теңдеу)
– екінші коэффициент
– бос мүше
Теңдеудің дискриминанті:
Егер D>0, онда теңдеудің екі түбірі бар: және
Түбірлердің қосындысы:
Түбірлердің көбейтіндісі:
. Сонымен,
– екінші коэффициент
– бос мүше
Теңдеудің дискриминанті:
Егер D>0, онда теңдеудің екі түбірі бар: және
Түбірлердің қосындысы:
Түбірлердің көбейтіндісі:
. Сонымен,
Слайд 7
Бұл теореманы бірінші дәлелдеген француз математигі Француа Виет (1540-1603) болғандықтан, соның
атымен аталады.
Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады.
Теорема (кері теорема). Егер сандары үшін шарттары орындалса, онда сандары теңдеуінің түбірлері болады.
Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады.
Теорема (кері теорема). Егер сандары үшін шарттары орындалса, онда сандары теңдеуінің түбірлері болады.
Слайд 8 Виет теоремасы және оған кері теорема теңдеуді шешпей-ақ
, түбірлерінің қосындысы мен көбейтіндісін табуға және түбірлері белгілі болғанда, теңдеуді құруға мүмкіндік береді.
Мысал қарастырайық:
Түбірлері және
болған квадраттық теңдеуді құрайық:
Мысал қарастырайық:
Түбірлері және
болған квадраттық теңдеуді құрайық:
Слайд 12х2 - 12х + с = 0 теңдеуінің бір түбірі х1=5.
х1+ х2=12 және х1 · х2=с. с-ны табыңдар.
х2 +рх + 15 = 0 теңдеуінің бір түбірі х1=3.
х1+ х2= -р және х1 · х2=15. р-ны табыңдар.
3. Теңдеулерді шешіп Виет теоремасы және кері теорема арқылы тексеріңдер:
а) х2 - 9х + 8 = 0,
б) х2 + 12х + 20 = 0,
в) х2 - 4х - 21 = 0.
Слайд 13Тест сұрақтары:
Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар:
А) 8; 15 В) -8; 15 С) 8; -15 D) -8; -15 Е) 5; -18
2. Түбірлері болатын теңдеуді жазыңдар:
А) В) С)
D) Е)
теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және
р-ны табыңдар.
А) 2; 5 В) -2; 5 С) -5; -2 D) 2; -5 Е) 5; -1.
4. Теңдеудің түбірлерін табыңдар:
А) 11; 10 В) -1; 10 С) 1; 10 D) 1; -10 Е) -1; -10
5. Келтірілген квадраттық теңдеуді көрсет:
А) В) С)
D) Е)