и
Тибилов Виталий
Руководитель: Абрамова т.в.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Арифметическая прогрессия (9 класс)
Содержание
- 1. Арифметическая прогрессия (9 класс)
- 2. Содержание презентации:ОпределениеВиды арифметической прогрессииФормула n-ого члена арифметического видаСвойство арифметической прогрессииФормула суммы первых n членов арифметической прогрессииЗадачиЗаключениеИсточники
- 3. В жизни часто бывает так, что величины
- 4. Арифметической прогрессией называется последовательность, каждый член которой,
- 5. Разность прогрессии:ИЛИ
- 6. Виды арифметической прогрессии:1) 3,6,9,12,15,18,21,24… d>0Возрастающая прогрессия.2) 7,7,7,7,7,7,7,7,7… d=0Постоянная прогрессия.3) 24,21,18,15,12,9,6,3… d
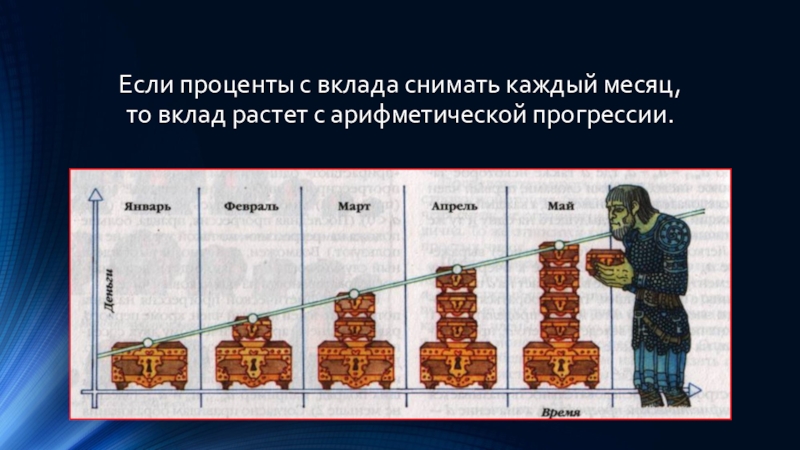
- 7. Если проценты с вклада снимать каждый месяц, то вклад растет с арифметической прогрессии.
- 8. Формула n-го члена арифметической прогрессииВывод: а2=а1+da3=a2+d=(a1+d)+d=a1+2da4=a3+d=(a1+2d)+d=a1+3da5=a4+d=(a1+3d)+d=a1+4d a100=a1+99d
- 9. Слайд 9
- 10.
- 11. Любая арифметическая прогрессия может быть задана формулой
- 12. Является ли арифметической прогрессией последовательность (аn), заданная формулой:1) an= 3n+1 2) an=n+43) an=-0,5n+1 4) an=n²+15) an=6n
- 13. Решение задачи К. Гауссом1 + 2 +
- 14. Этим способом находят сумму любой арифметической прогрессии.
- 15. Формула суммы первых n членов арифметической прогрессииSn=a1 +a2 + a3+ a4 +…+an-1+anSn=an+an-1+an-2+an-3…+a2+a1a1+an=a2+an-1=a3+an-2=…=an-1+a2=an+a12sn=(a1+an)∙n
- 16. Сумма n-первых членов арифметической прогрессии:
- 17. Знание формулы суммы n первых членов арифметической
- 18. Задача:При хранении бревен строевого леса их укладывают
- 19. Теперь найдём сумму первых n нечётных натуральных
- 20. Найти сумму первых 100 членов арифметической прогрессии.
- 21. ЗадачаВосхождение на вершину горы группа альпинистов осуществило
- 22. Слайд 22
- 23. Восхождение на вершину горы группа альпинистов осуществило
- 24. Арифметическая прогрессия
- 25. Источники:Учебник по алгебре (9 кл.) Макарычев; Миндюк; Нешков; Суворова.Поисковая система Yandex.ru (изображения)Википедия
- 26. Спасибо за просмотр!!!
Содержание презентации:ОпределениеВиды арифметической прогрессииФормула n-ого члена арифметического видаСвойство арифметической прогрессииФормула суммы первых n членов арифметической прогрессииЗадачиЗаключениеИсточники
Слайд 1Презентация по математике на тему:
«Арифметическая прогрессия»
Презентацию подготовили
Ученики мбоу школы №4
Спесивцев Дмитрий
Слайд 2Содержание презентации:
Определение
Виды арифметической прогрессии
Формула n-ого члена арифметического вида
Свойство арифметической прогрессии
Формула суммы
первых n членов арифметической прогрессии
Задачи
Заключение
Источники
Задачи
Заключение
Источники
Слайд 3В жизни часто бывает так, что величины изменяются с течением времени
на одно и то же значение.
Когда поезд едет со скоростью 80 км/ч, он за каждый час увеличивает пройденный путь на одну и ту же величину.
Человек с каждым годом жизни увеличивает свой возраст на одно и то же время, которое суждено прожить на этом свете.
И даже толстяк, безуспешно применяющий модные диеты, каждые сутки изменяет свой вес на одну и ту же величину- на нуль килограммов.
Когда поезд едет со скоростью 80 км/ч, он за каждый час увеличивает пройденный путь на одну и ту же величину.
Человек с каждым годом жизни увеличивает свой возраст на одно и то же время, которое суждено прожить на этом свете.
И даже толстяк, безуспешно применяющий модные диеты, каждые сутки изменяет свой вес на одну и ту же величину- на нуль килограммов.
Слайд 4
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен
предыдущему члену, сложенному с одним и тем же числом.
an+1 = an + d , n є N
Число d называют разностью арифметической прогрессии.
d = an+1 - an
an+1 = an + d , n є N
Число d называют разностью арифметической прогрессии.
d = an+1 - an
Слайд 6Виды арифметической прогрессии:
1) 3,6,9,12,15,18,21,24… d>0
Возрастающая прогрессия.
2) 7,7,7,7,7,7,7,7,7… d=0
Постоянная прогрессия.
3) 24,21,18,15,12,9,6,3… d
Слайд 8Формула n-го члена арифметической
прогрессии
Вывод:
а2=а1+d
a3=a2+d=(a1+d)+d=a1+2d
a4=a3+d=(a1+2d)+d=a1+3d
a5=a4+d=(a1+3d)+d=a1+4d
a100=a1+99d
Слайд 11Любая арифметическая прогрессия может быть задана формулой вида:
аn=kn+b, где k и
b некоторые числа.
Верно и обратное:
последовательность заданная формулой вида:
аn=kn+b, где k и b некоторые числа, является арифметической прогрессией.
Верно и обратное:
последовательность заданная формулой вида:
аn=kn+b, где k и b некоторые числа, является арифметической прогрессией.
Слайд 12Является ли арифметической прогрессией последовательность (аn), заданная формулой:
1) an= 3n+1
2) an=n+4
3)
an=-0,5n+1
4) an=n²+1
5) an=6n
4) an=n²+1
5) an=6n
Слайд 13Решение задачи К. Гауссом
1 + 2 + 3 +4+…+97+ 98 +
99 + 100
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
Таких сумм здесь 50.
1+2+3+4+…+97+98+99+100=101*50=5050
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
Таких сумм здесь 50.
1+2+3+4+…+97+98+99+100=101*50=5050
Слайд 14Этим способом находят сумму любой арифметической прогрессии. Ведь ее особенность состоит
в том, что, переходя от суммы двух крайних членов а1+аn к сумме их соседей а2+аn-1, получается то же самое число.
Слайд 15Формула суммы первых n членов
арифметической прогрессии
Sn=a1 +a2 + a3+ a4 +…+an-1+an
Sn=an+an-1+an-2+an-3…+a2+a1
a1+an=a2+an-1=a3+an-2=…=an-1+a2=an+a1
2sn=(a1+an)∙n
Слайд 17Знание формулы суммы n первых членов арифметической прогрессии позволяет решать не
мало различных задач. Например, найти сумму первых n натуральных чисел для произвольного n. Воспользуемся первой формулой:
Слайд 18Задача:
При хранении бревен строевого леса их укладывают так, как показано на
рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?
Решение:
Кладку бревен рассмотрим в виде арифметической прогрессии, где а1= 1, а2= 2, аn= 12
d = 2 – 1 = 1
an = a1+ d · (n - 1)
12 = 1 + n – 1
n = 12 S12=78
Ответ: 78 бревен.
Решение:
Кладку бревен рассмотрим в виде арифметической прогрессии, где а1= 1, а2= 2, аn= 12
d = 2 – 1 = 1
an = a1+ d · (n - 1)
12 = 1 + n – 1
n = 12 S12=78
Ответ: 78 бревен.
Слайд 19Теперь найдём сумму первых n нечётных натуральных чисел. Здесь можно использовать
вторую формулу для суммы. Искомая сумма оказывается равной
Не правда ли, удивительно: сумма первых n нечётных чисел в точности равна квадрату их количества!
Слайд 21Задача
Восхождение на вершину горы группа альпинистов осуществило за 7 дней, каждый
день поднимаясь на некоторое одинаковое количество метров меньше, чем в предыдущий.
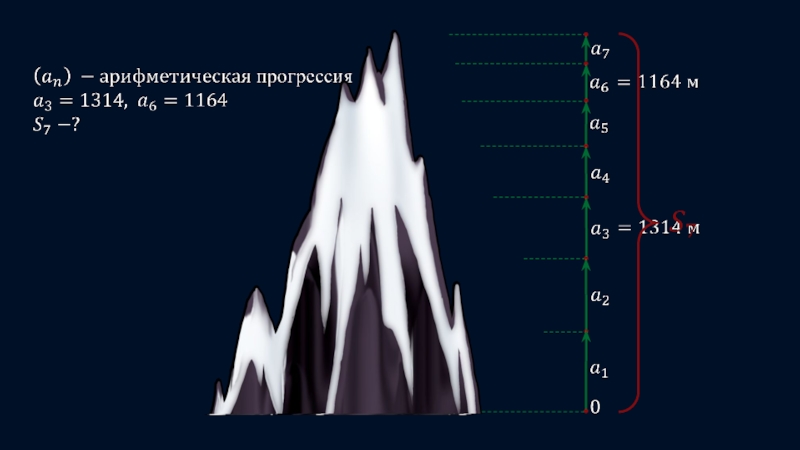
Какова высота горы, если за третий день они поднялись на 1314 метров, а за шестой день — на 1164 метра?
Какова высота горы, если за третий день они поднялись на 1314 метров, а за шестой день — на 1164 метра?
Слайд 23Восхождение на вершину горы группа альпинистов осуществило за 7 дней, каждый
день поднимаясь на некоторое одинаковое количество метров меньше, чем в предыдущий.
Какова высота горы, если за третий день они поднялись на 1314 метров,
а за шестой день — на 1164 метра?
Какова высота горы, если за третий день они поднялись на 1314 метров,
а за шестой день — на 1164 метра?
Слайд 25Источники:
Учебник по алгебре (9 кл.) Макарычев; Миндюк; Нешков; Суворова.
Поисковая система Yandex.ru
(изображения)
Википедия
Википедия