Шар
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Сфера и шар.
Содержание
- 1. Сфера и шар.
- 2. История возникновенияИз истории возникновения. Шаром принято называть
- 3. Сфера и шар в жизни людей
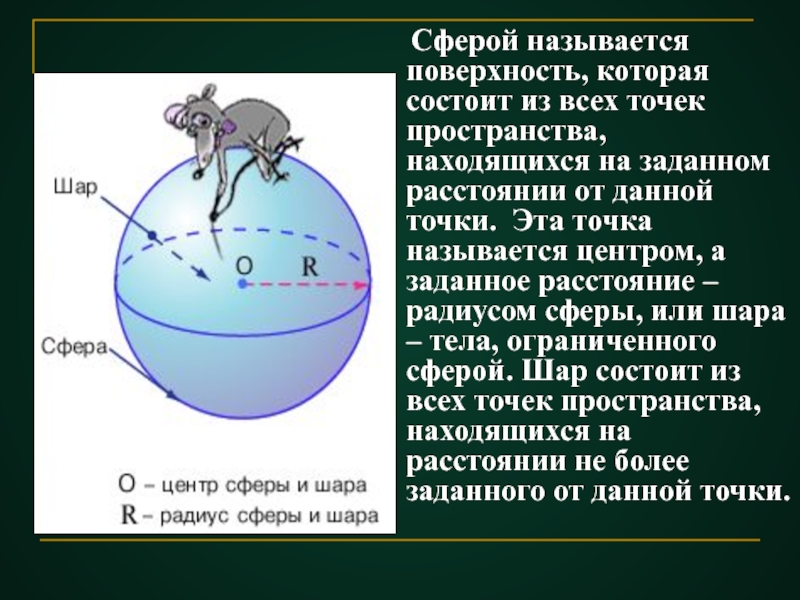
- 4. Сферой называется поверхность, которая состоит
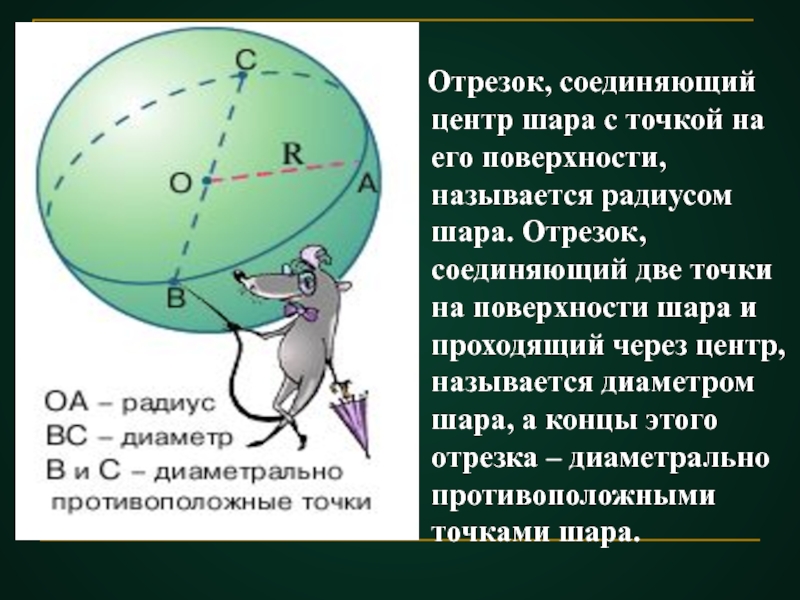
- 5. Отрезок, соединяющий центр шара с
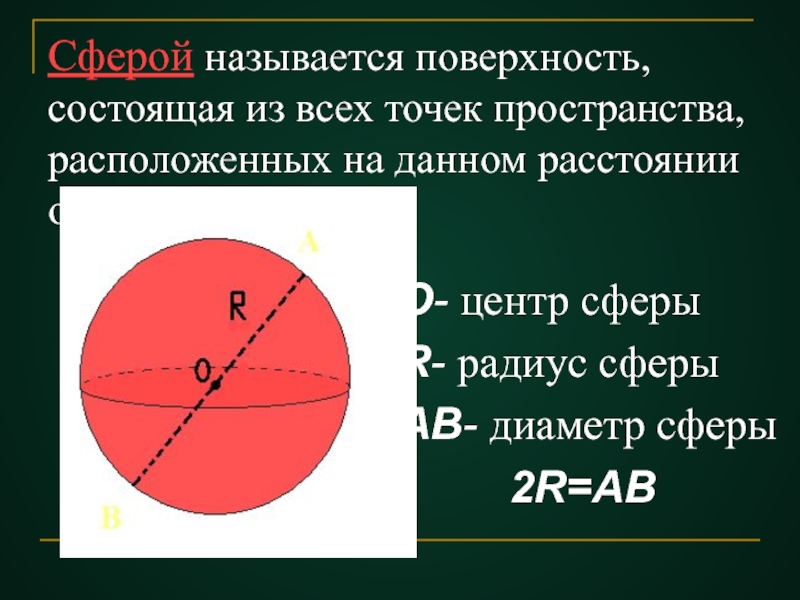
- 6. Сферой называется поверхность, состоящая из всех точек
- 7. Сферу можно получить вращением полуокружности АСВ вокруг диаметра АВ
- 8. Шаром называется тело ограниченное сферой.Центр, радиус и диаметр сферы называются также диаметром шара.Шар
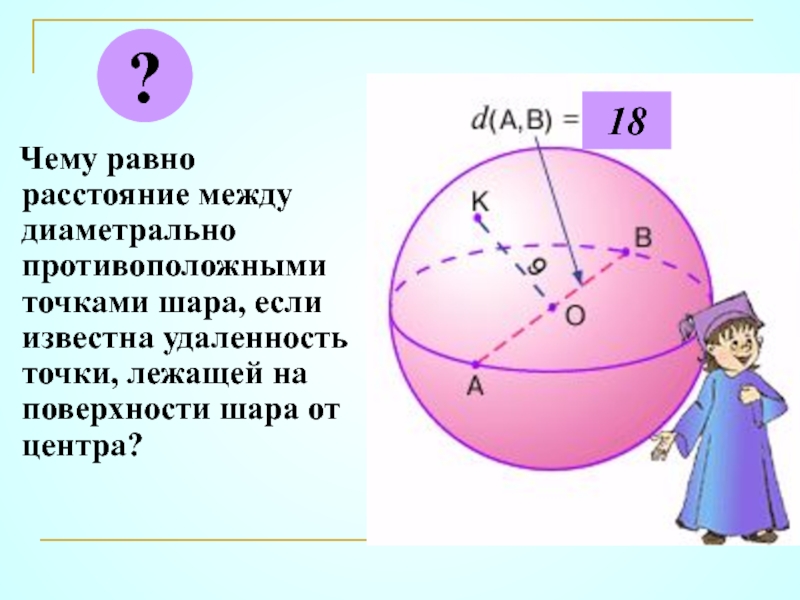
- 9. Чему равно расстояние между диаметрально
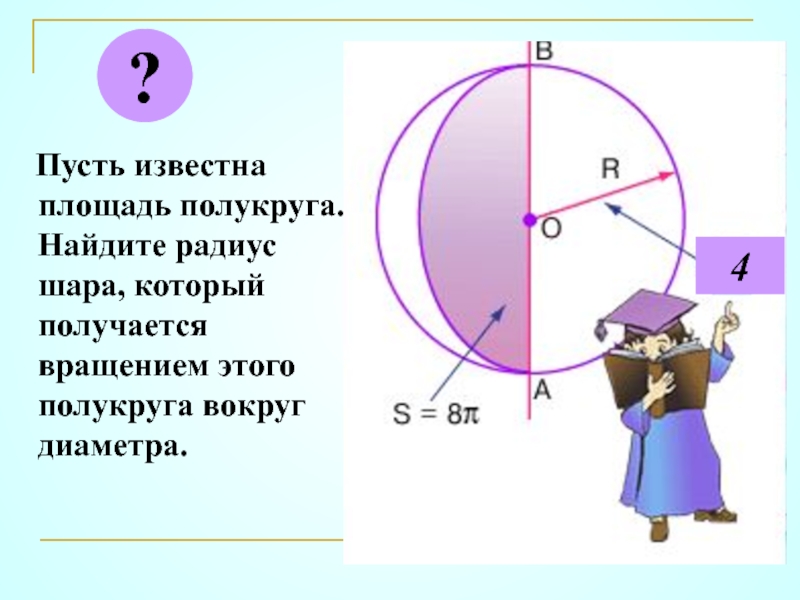
- 10. Пусть известна площадь полукруга. Найдите радиус шара, который получается вращением этого полукруга вокруг диаметра.?4
- 11. Теорема. Любое сечение шара плоскостью есть круг.
- 12. Доказательство: Рассмотрим прямоугольный треугольник, вершинами которого
- 13. Следствие. Если известны радиус шара и расстояние
- 14. Пусть известны диаметр шара и
- 15. Задана прямоугольная система координат Оху и дана
- 16. Выведем уравнение сферы радиуса R с центром
- 17. Расстояние от произвольной точки M (x; y;
- 18. Если точка М лежит на данной сфере
- 19. В прямоугольной системе координат уравнение сферы радиуса
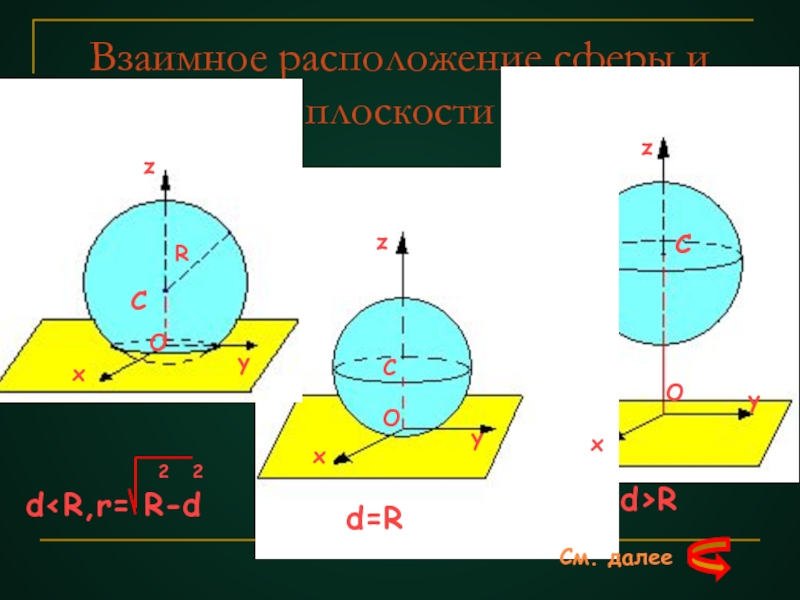
- 20. Взаимное расположение сферы и плоскости Исследуем
- 21. Взаимное расположение сферы и плоскостиzyxOCRyxzCzyxCOO 2 2dRСм. далее
- 22. Пусть радиус сферы - R, а расстояние
- 23. z=0 х2+у 2+(z-d)2=R2Составим систему уравнений :Подставив
- 24. Возможны три случая :1) d0,
- 25. Итак, если расстояние от центра сферы до
- 26. Ясно, что сечение шара плоскостью является круг.Если
- 27. Если секущая плоскость не проходит через центр
- 28. 2) d=R,тогда R2-d2=0, и уравнению
- 29. Итак, если расстояние от центра сферы до
- 30. 3) d>R, тогда R2-d2
- 31. Следовательно, если расстояние от центра сферы
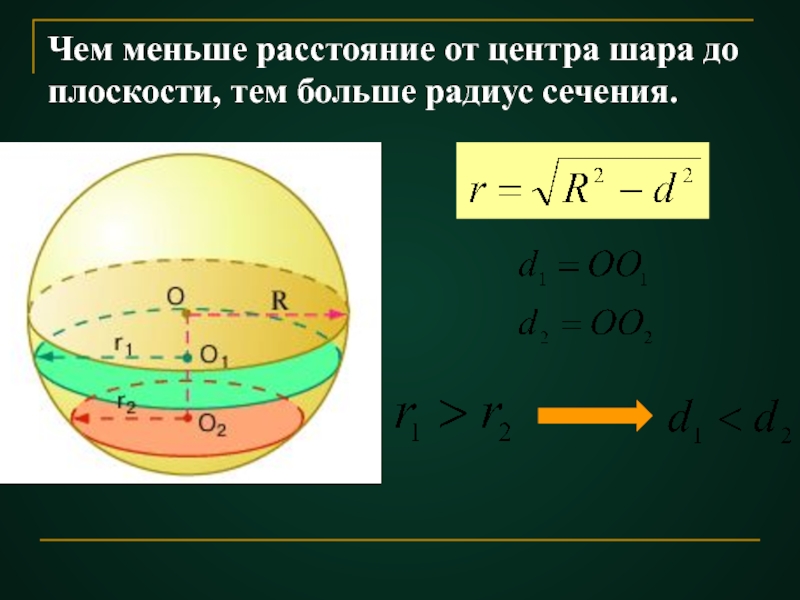
- 32. Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения.
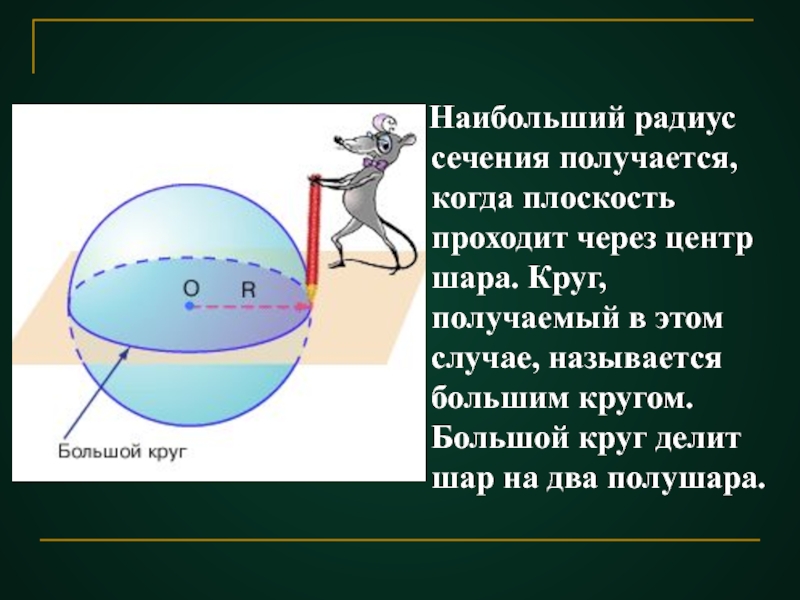
- 33. Наибольший радиус сечения получается, когда
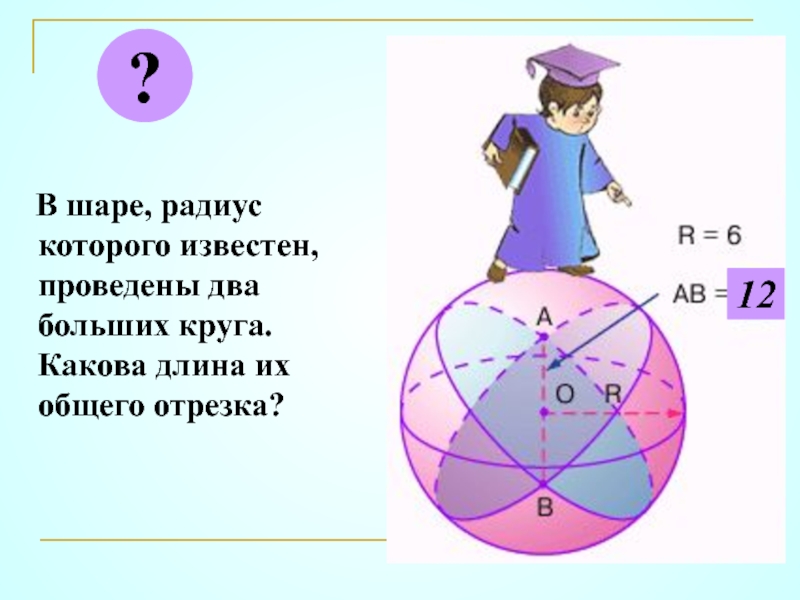
- 34. В шаре, радиус которого известен, проведены два больших круга. Какова длина их общего отрезка??12
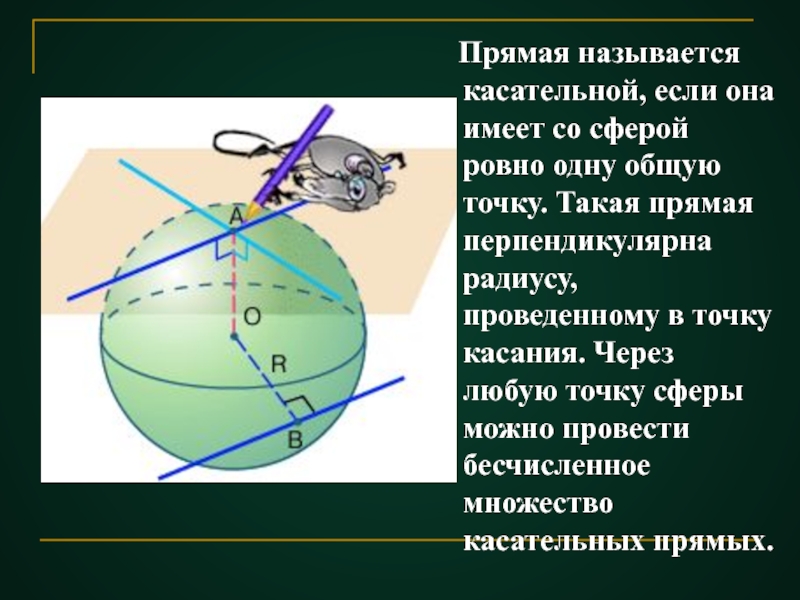
- 35. Прямая называется касательной, если она
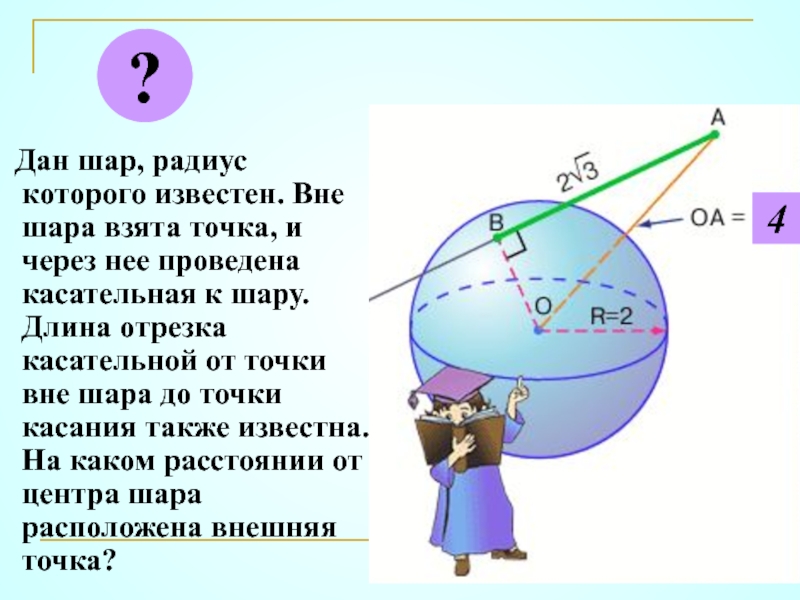
- 36. Дан шар, радиус которого известен.
- 37. Взаимное расположение двух шаров. Если два
- 38. Касание шаров может быть внутренним и внешним.
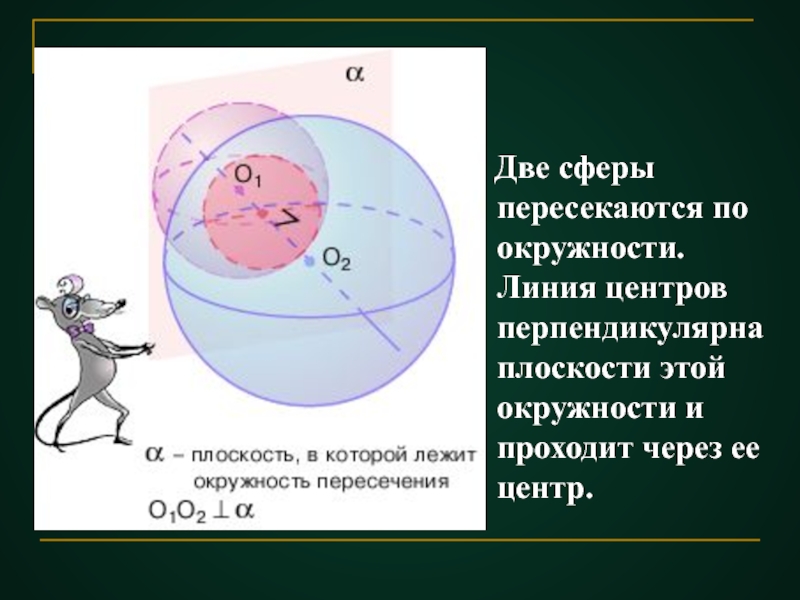
- 39. Две сферы пересекаются по окружности.
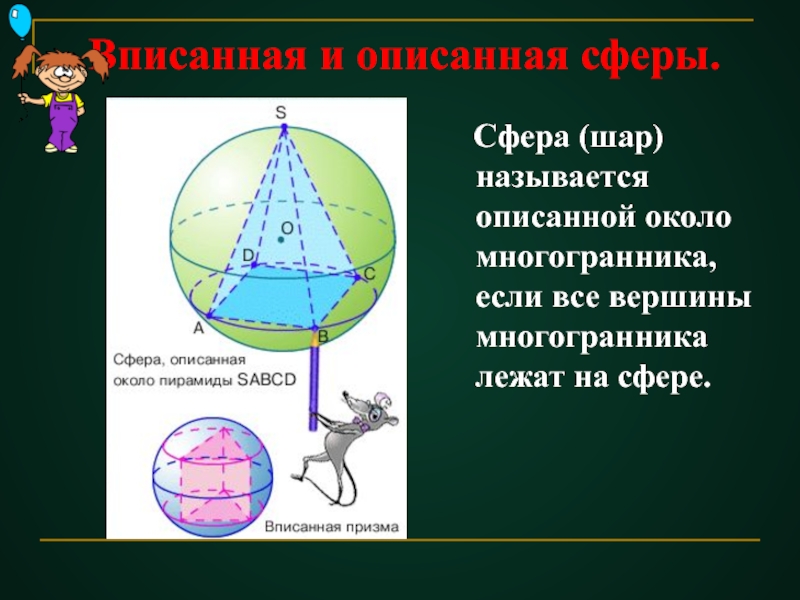
- 40. Вписанная и описанная сферы. Сфера (шар)
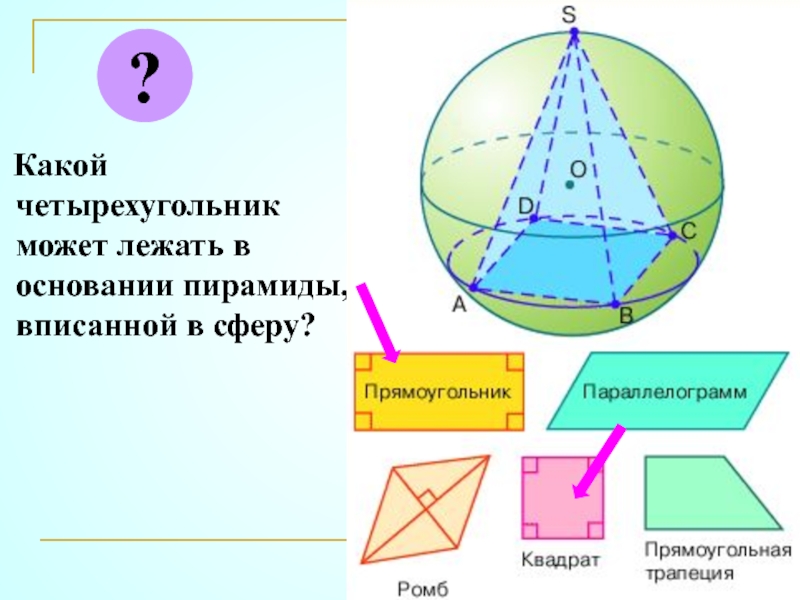
- 41. Какой четырехугольник может лежать в основании пирамиды, вписанной в сферу??
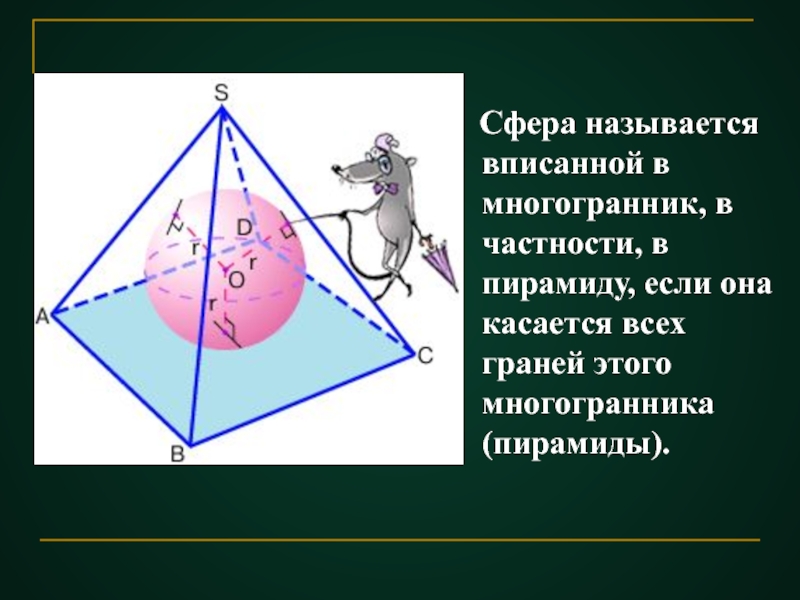
- 42. Сфера называется вписанной в многогранник,
- 43. В основании треугольной пирамиды лежит
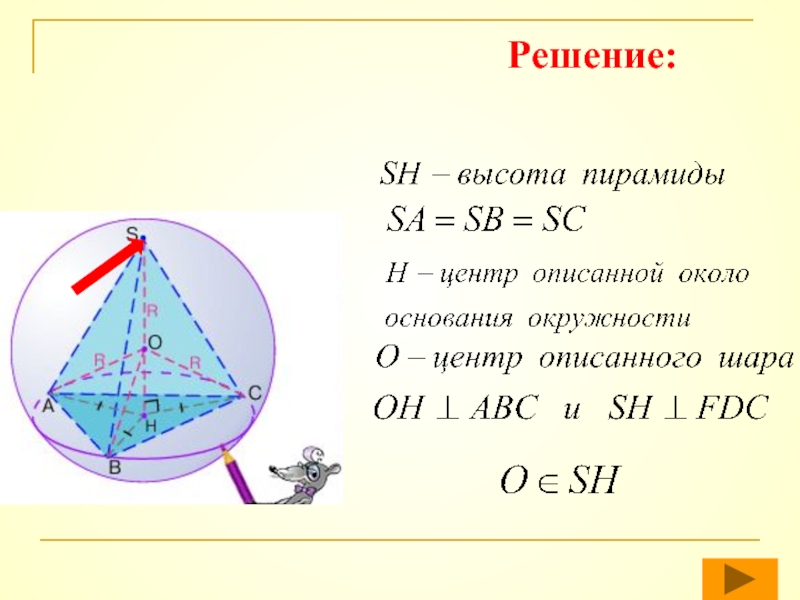
- 44. Решение:
- 45. I этап. Нахождение радиуса вписанного шара1)
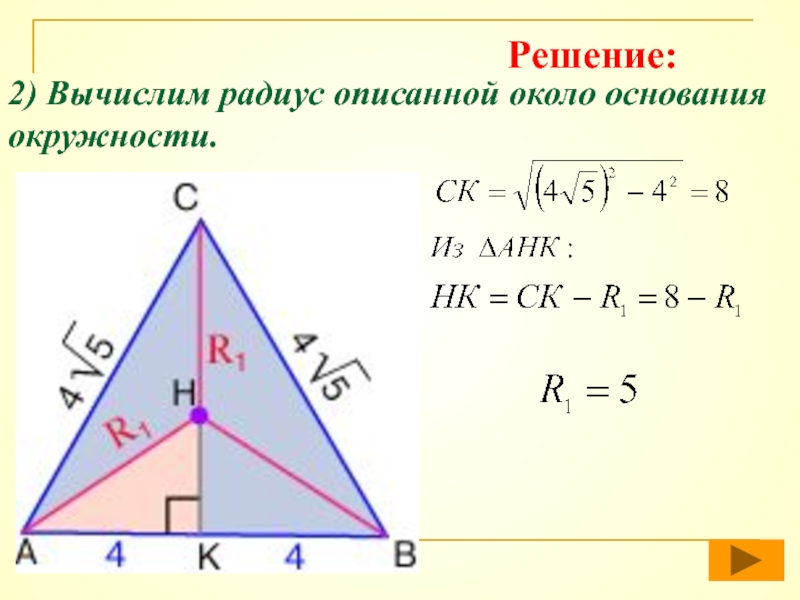
- 46. 2) Вычислим радиус описанной около основания окружности.Решение:
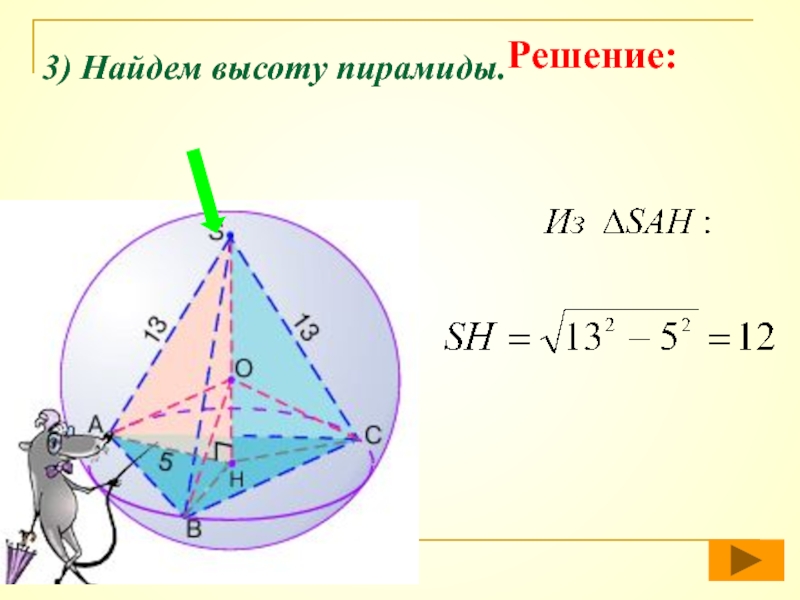
- 47. 3) Найдем высоту пирамиды.Решение:
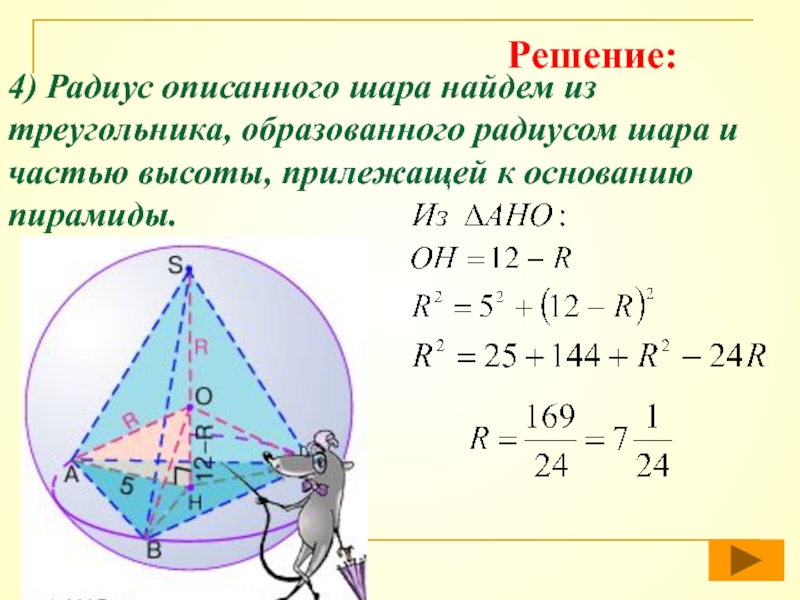
- 48. 4) Радиус описанного шара найдем из треугольника,
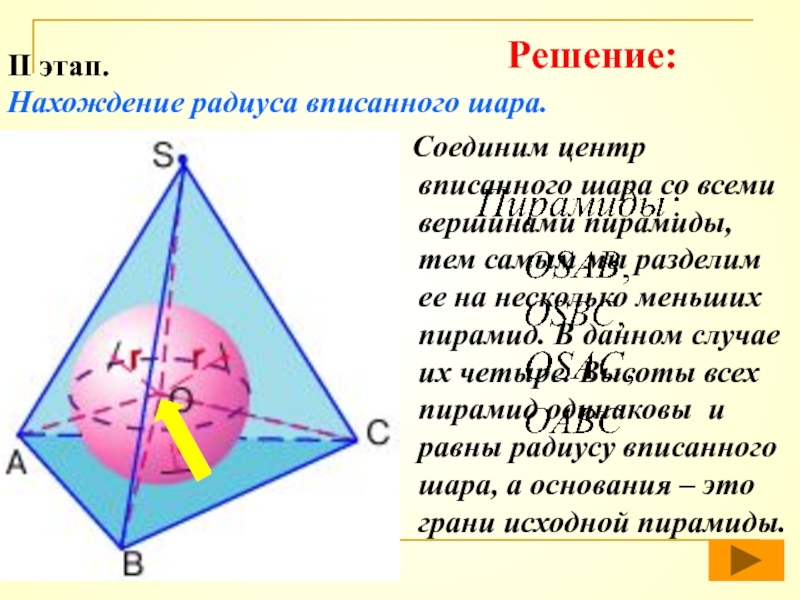
- 49. Соединим центр вписанного шара со
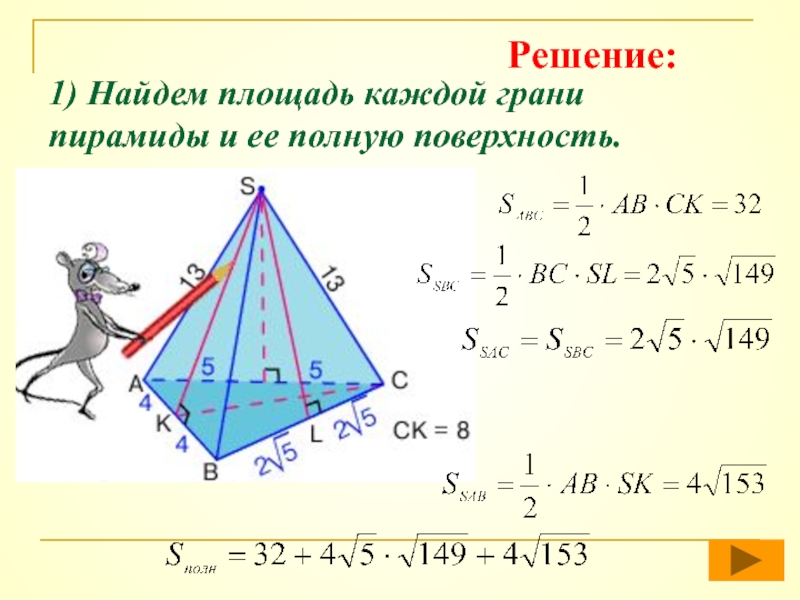
- 50. 1) Найдем площадь каждой грани пирамиды и ее полную поверхность.Решение:
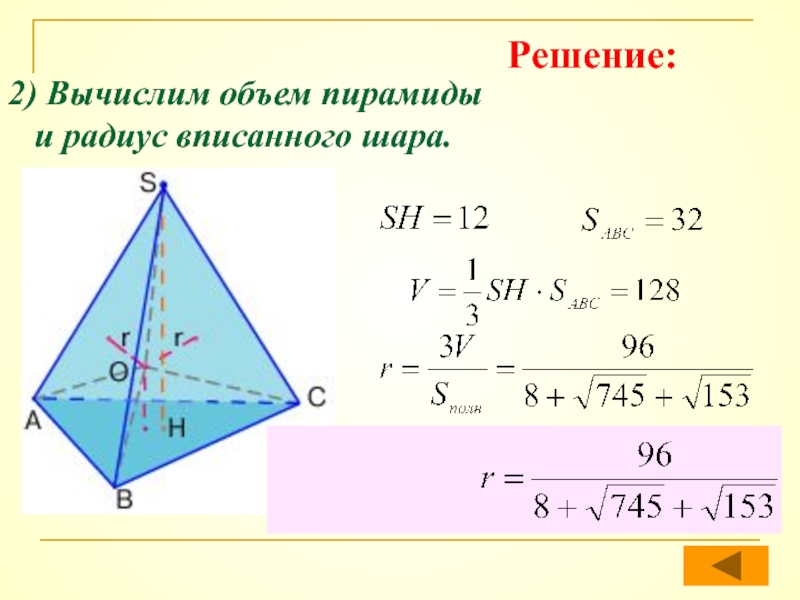
- 51. 2) Вычислим объем пирамиды и радиус вписанного шара.Решение:
История возникновенияИз истории возникновения. Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова «
Слайд 2История возникновения
Из истории возникновения. Шаром принято называть тело, ограниченное сферой, т.е.
шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» - мяч. При этом слово « шар» образовалось от перехода согласных сф в ш. В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы. Сфера всегда широко применялось в различных областях науки и техники.
Слайд 4 Сферой называется поверхность, которая состоит из всех точек пространства,
находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.
Слайд 5 Отрезок, соединяющий центр шара с точкой на его поверхности,
называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.
Слайд 6Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном
расстоянии от данной точки.
О- центр сферы
R- радиус сферы
АВ- диаметр сферы
2R=АВ
Слайд 8Шаром называется тело ограниченное сферой.
Центр, радиус и диаметр сферы называются также
диаметром шара.
Шар
Слайд 9 Чему равно расстояние между диаметрально противоположными точками шара, если
известна удаленность точки, лежащей на поверхности шара от центра?
?
18
Слайд 10 Пусть известна площадь полукруга. Найдите радиус шара, который получается
вращением этого полукруга вокруг диаметра.
?
4
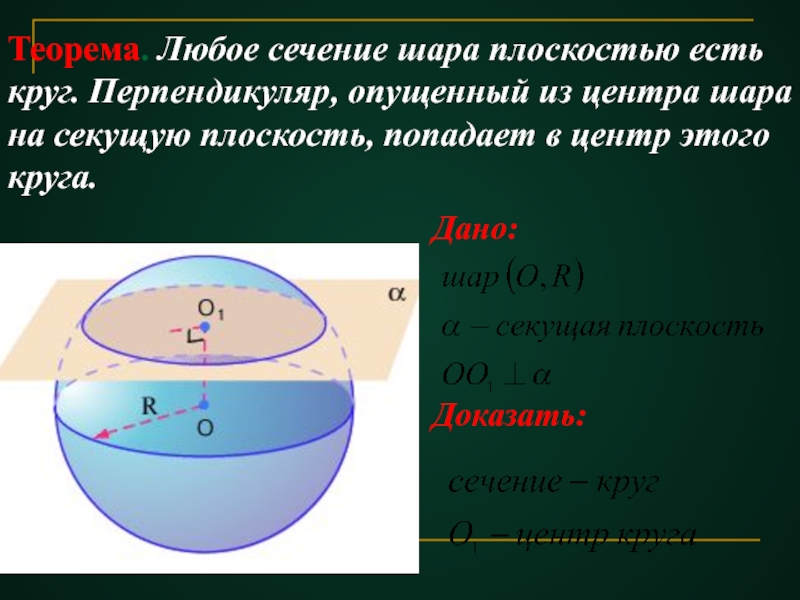
Слайд 11Теорема. Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра
шара на секущую плоскость, попадает в центр этого круга.
Дано:
Доказать:
Слайд 12Доказательство:
Рассмотрим прямоугольный треугольник, вершинами которого являются центр шара, основание
перпендикуляра, опущенного из центра на плоскость, и произвольная точка сечения.
Слайд 13Следствие. Если известны радиус шара и расстояние от центра шара до
плоскости сечения, то радиус сечения вычисляется по теореме Пифагора.
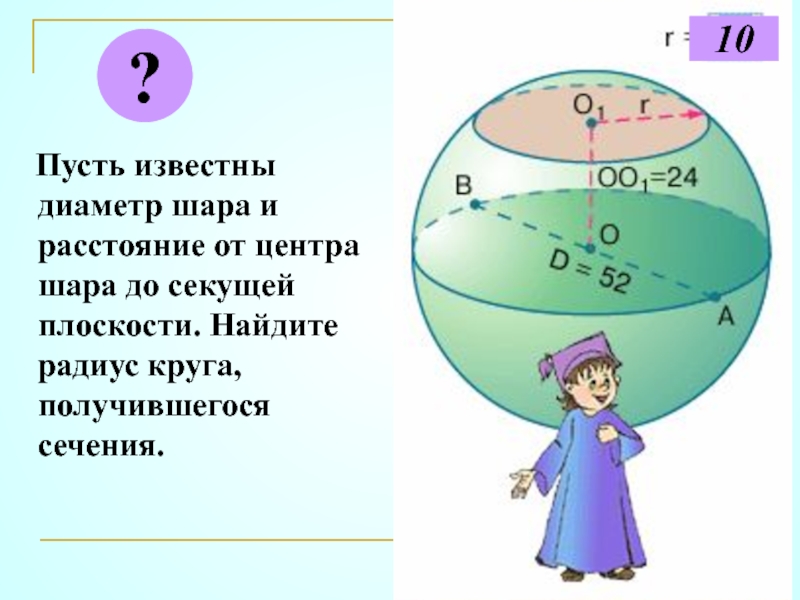
Слайд 14 Пусть известны диаметр шара и расстояние от центра шара
до секущей плоскости. Найдите радиус круга, получившегося сечения.
?
10
Слайд 15Задана прямоугольная система координат Оху и дана некоторая поверхность F, например
плоскость или сфера . Уравнение с тремя переменными x, у, z называется уравнением поверхности F и не удовлетворяют координаты никакой точки , не лежащей на этой поверхности .
Уравнение сферы
См. далее
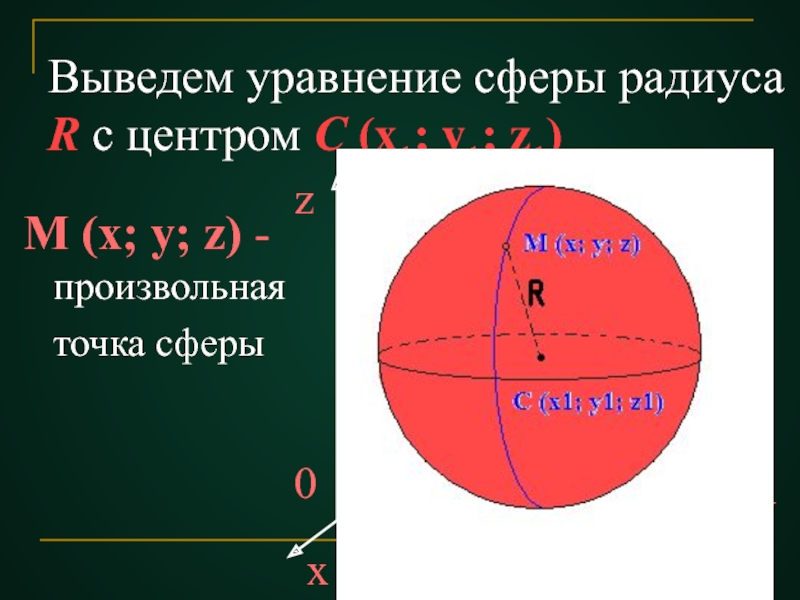
Слайд 16Выведем уравнение сферы радиуса R с центром С (x1; y1; z1)
M (x; y; z) -произвольная точка сферы
x
z
y
0
Слайд 17Расстояние от произвольной точки M (x; y; z)до точки С вычисляем
по формуле
МС=√(x-x1)2+(y-y1)2+(z-z1)2
Слайд 18Если точка М лежит на данной сфере , то МС=R, или
МС2=R2 т.е. координаты точки М удовлетворяют уравнению:
R2=(x-x1)2+(y-y1)2+(z-z1)2
R2=(x-x1)2+(y-y1)2+(z-z1)2
Если точка М не лежит на данной сфере , то МС2= R2 т.е. координаты точки М не удовлетворяют данного уравнения.
Слайд 19В прямоугольной системе координат уравнение сферы радиуса R с центром С
(x1; y1; z1) имеет вид
R2=(x-x1)2+(y-y1)2+(z-z1)2
Слайд 20Взаимное расположение сферы и плоскости
Исследуем взаимное расположение сферы и
плоскости в зависимости от соотношения между радиусом сферы и расстоянием от её центра до плоскости.
Слайд 22Пусть радиус сферы - R, а расстояние от её центра до
плоскости a - d
Введём систему координат, так чтобы плоскость Оху совпадала с плоскостью α ,а центр сферы лежал по Оz , тогда уравнение плоскости α :z=0, а уравнение сферы с учётом (С имеет координаты (0;0;d) )
х2+у 2+(z-d)2=R2
Слайд 23z=0
х2+у 2+(z-d)2=R2
Составим систему уравнений :
Подставив z=0 во второе уравнение ,
получим :
х2+у 2=R2-d2
х2+у 2=R2-d2
Слайд 24Возможны три случая :
1) d
R2-d2>0,
и уравнение
х2+у 2=R2-d2 является уравнением окружности r = √R2-d2 с центром в точке О на плоскости Оху.
В данном случае сфера и плоскость пересекаются по окружности.
и уравнение
х2+у 2=R2-d2 является уравнением окружности r = √R2-d2 с центром в точке О на плоскости Оху.
В данном случае сфера и плоскость пересекаются по окружности.
Слайд 25Итак, если расстояние от центра сферы до плоскости меньше радиуса сферы,
то сечение сферы плоскостью есть окружность .
Слайд 26Ясно, что сечение шара плоскостью является круг.
Если секущая плоскость проходит через
центр шара, то d=0 и в сечении получается круг радиуса R, т.е. круг , радиус которого равен радиусу шара. Такой круг называется большим кругом шара.
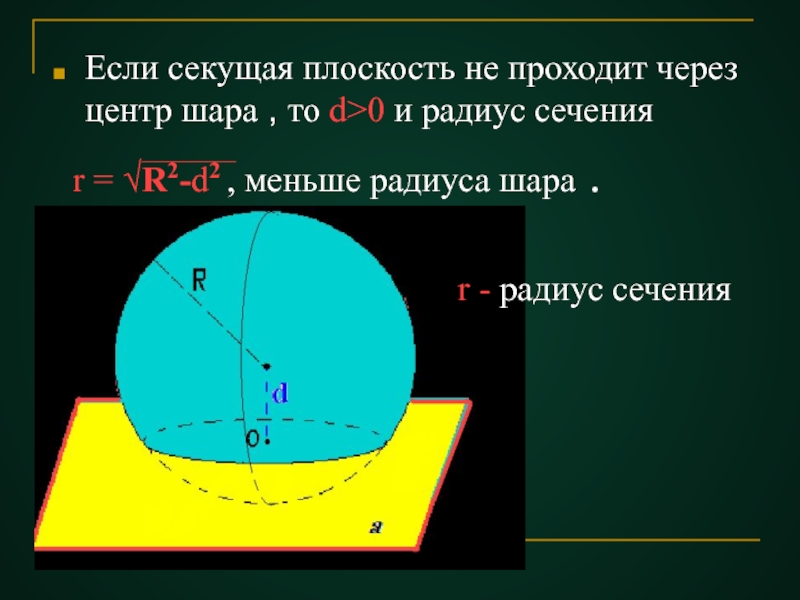
Слайд 27Если секущая плоскость не проходит через центр шара , то d>0
и радиус сечения
r = √R2-d2 , меньше радиуса шара .
r = √R2-d2 , меньше радиуса шара .
r - радиус сечения
Слайд 28 2) d=R,тогда R2-d2=0, и уравнению удовлетворяют только
х=0,
у=0,
а значит О(0;0;0)удовлетворяют обоим уравнениям ,т.е.
О- единственная общая точка сферы и плоскости .
а значит О(0;0;0)удовлетворяют обоим уравнениям ,т.е.
О- единственная общая точка сферы и плоскости .
Слайд 29Итак, если расстояние от центра сферы до плоскости равно радиусу сферы
, то сфера и плоскость имеют только одну общую точку.
Слайд 31Следовательно, если расстояние от центра сферы до плоскости больше радиуса сферы,
то сфера и плоскость не имеют общих точек.
Слайд 33 Наибольший радиус сечения получается, когда плоскость проходит через центр
шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.
Слайд 34 В шаре, радиус которого известен, проведены два больших круга.
Какова длина их общего отрезка?
?
12
Слайд 35 Прямая называется касательной, если она имеет со сферой ровно
одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.
Слайд 36 Дан шар, радиус которого известен. Вне шара взята точка,
и через нее проведена касательная к шару. Длина отрезка касательной от точки вне шара до точки касания также известна. На каком расстоянии от центра шара расположена внешняя точка?
?
4
Слайд 37Взаимное расположение двух шаров.
Если два шара или сферы имеют
только одну общую точку, то говорят, что они касаются. Их общая касательная плоскость перпендикулярна линии центров (прямой, соединяющей центры обоих шаров).
Слайд 39 Две сферы пересекаются по окружности. Линия центров перпендикулярна плоскости
этой окружности и проходит через ее центр.
Слайд 40Вписанная и описанная сферы.
Сфера (шар) называется описанной около многогранника,
если все вершины многогранника лежат на сфере.
Слайд 42 Сфера называется вписанной в многогранник, в частности, в пирамиду,
если она касается всех граней этого многогранника (пирамиды).
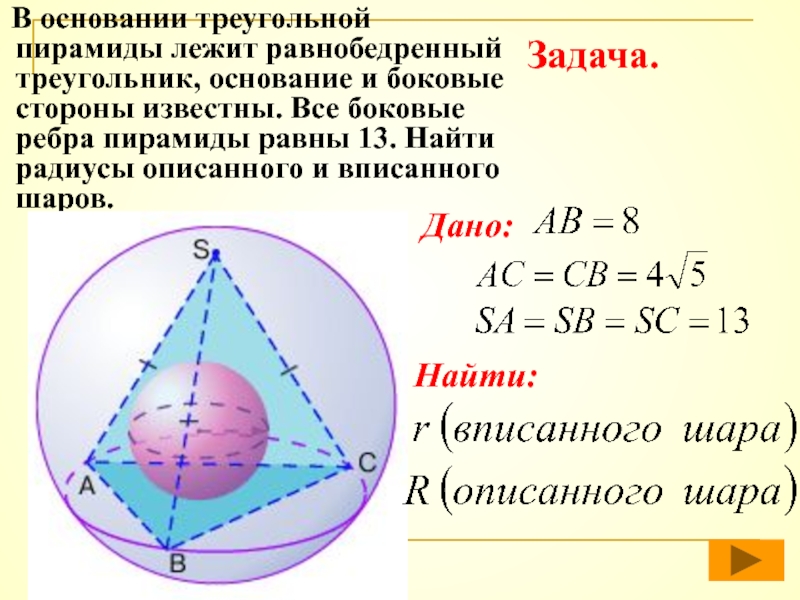
Слайд 43 В основании треугольной пирамиды лежит равнобедренный треугольник, основание и
боковые стороны известны. Все боковые ребра пирамиды равны 13. Найти радиусы описанного и вписанного шаров.
Задача.
Дано:
Найти:
Слайд 45I этап.
Нахождение радиуса вписанного шара
1) Центр описанного шара удален от
всех вершин пирамиды на одинаковое расстояние, равное радиусу шара, и в частности, от вершин треугольника АВС. Поэтому он лежит на перпендикуляре к плоскости основания этого треугольника, который восстановлен из центра описанной окружности. В данном случае этот перпендикуляр совпадает с высотой пирамиды, поскольку ее боковые ребра равны.
Слайд 484) Радиус описанного шара найдем из треугольника, образованного радиусом шара и
частью высоты, прилежащей к основанию пирамиды.
Решение:
Слайд 49 Соединим центр вписанного шара со всеми вершинами пирамиды, тем
самым мы разделим ее на несколько меньших пирамид. В данном случае их четыре. Высоты всех пирамид одинаковы и равны радиусу вписанного шара, а основания – это грани исходной пирамиды.
Решение:
II этап.
Нахождение радиуса вписанного шара.
