Работу подготовила ученица 7-А класса МБОУ «СОШ№5» г.Красноперекопска.
Руководитель Шеина Е.Н., учитель математики
МБОУ «СОШ№5»
г.Красноперекопска.
2017год.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
Содержание
- 1. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
- 2. Обоснование выбора темы
- 3. Немного из истории Леонард Эйлер, крупнейший
- 4. Из теории множеств Множеством
- 5. Из теории множеств Пересечением множеств A
- 6. Из теории множествВАОбъединением множеств A и B
- 7. Решение задач с помощью кругов Эйлера
- 8. Задача № 1. Из 52 школьников
- 9. Задача №2.Некоторые ребята из нашего класса любят
- 10. Задача №3 . На полке
- 11. Решение Так как Гарри Поттер всего прочитал
- 12. Задача №4 . Сколько человек участвует
- 13. Решение3+7+1+2+5+6+6==30(чел) - участвовали в прогулке и
- 14. Задача №5. В классе 30
- 15. РешениеМХ-2А х-612-ХХ10-Х9-ХТ Х+4В классе
- 16. Решение Пусть х человек пользуется всеми
- 17. 2 способРешение 20+15+23-10-12-9+х=30, 27+х=30, х=3Ответ: 3 человекаХМАТ20152310129
- 18. Заключение В моей работе рассмотрены задачи,
- 19. Список используемой литературы: 1. Гаврилова Т. Д..Занимательная
Слайд 1
Слайд 2 Обоснование выбора темы
Существует множество приемов, которые
Цель работы:
- познакомится с кругами Эйлера – Венна;
-научиться применять способ решения задач с помощью кругов Эйлера – Венна;
-составлять задачи практического содержания.
Слайд 3Немного из истории
Леонард Эйлер, крупнейший математик XVIII в., родился
Наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна.
Слайд 4Из теории множеств
Множеством называют произвольную совокупность объектов,
Над множествами можно выполнять определенные действия: находить их пересечение и объединение.
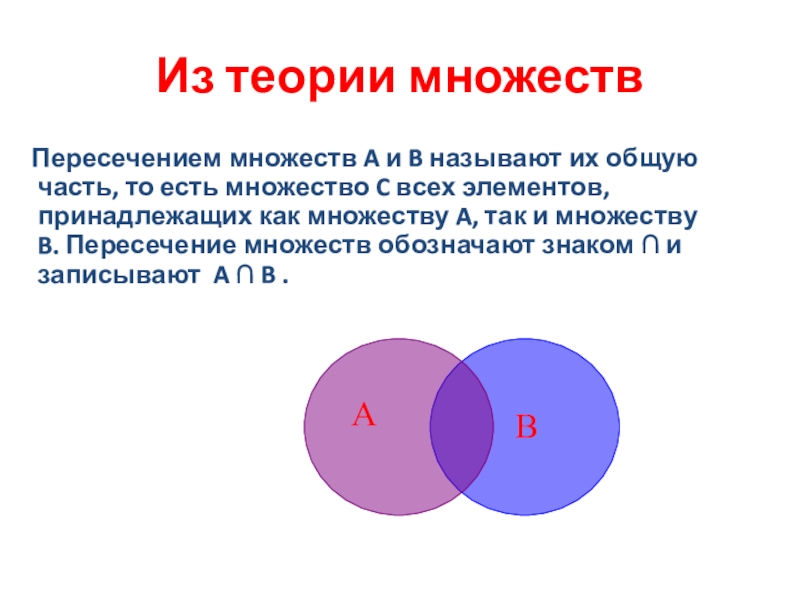
Слайд 5Из теории множеств
Пересечением множеств A и B называют их
А
В
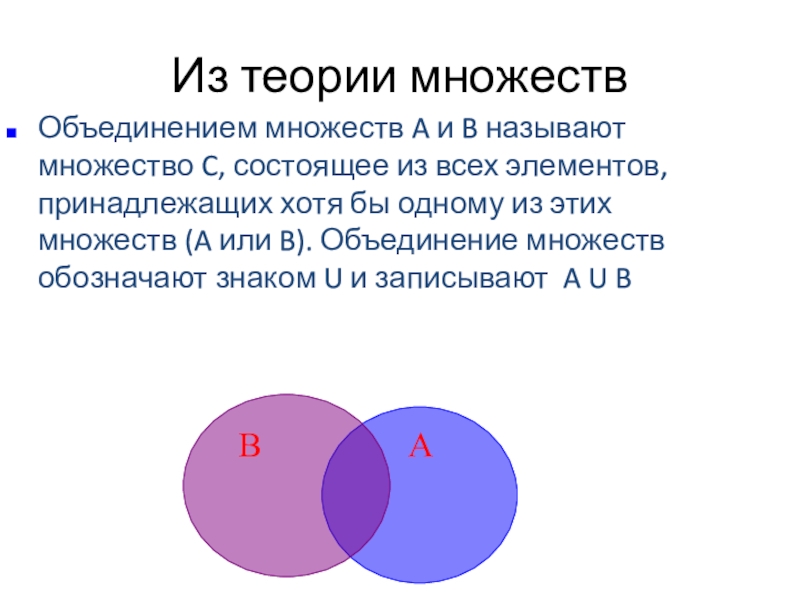
Слайд 6Из теории множеств
В
А
Объединением множеств A и B называют множество C, состоящее
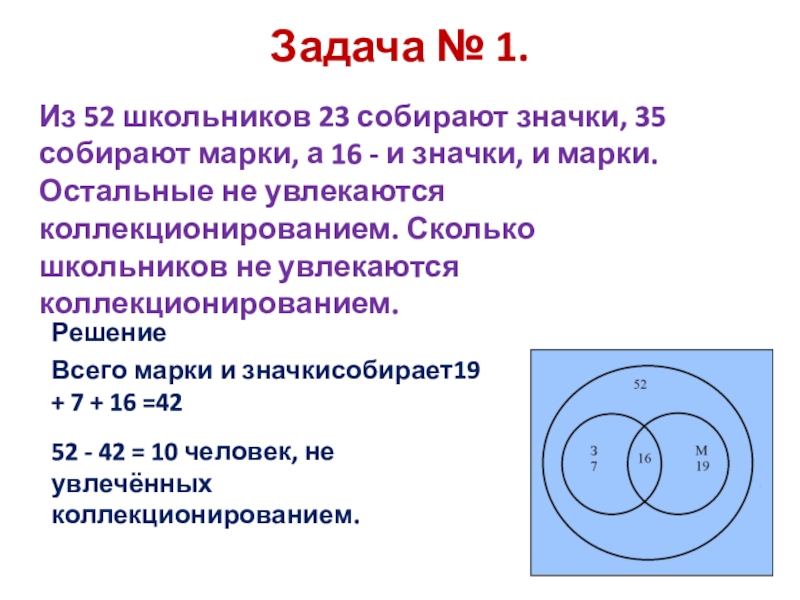
Слайд 8Задача № 1.
Из 52 школьников 23 собирают значки, 35 собирают
Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием.
Решение
Всего марки и значкисобирает19 + 7 + 16 =42
52 - 42 = 10 человек, не увлечённых коллекционированием.
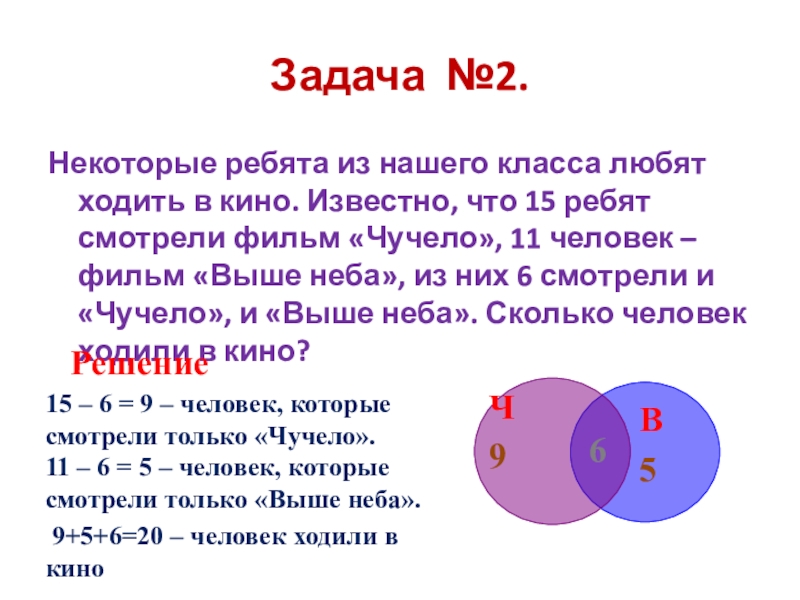
Слайд 9Задача №2.
Некоторые ребята из нашего класса любят ходить в кино. Известно,
Ч
9
6
В
5
Решение
15 – 6 = 9 – человек, которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».
9+5+6=20 – человек ходили в кино
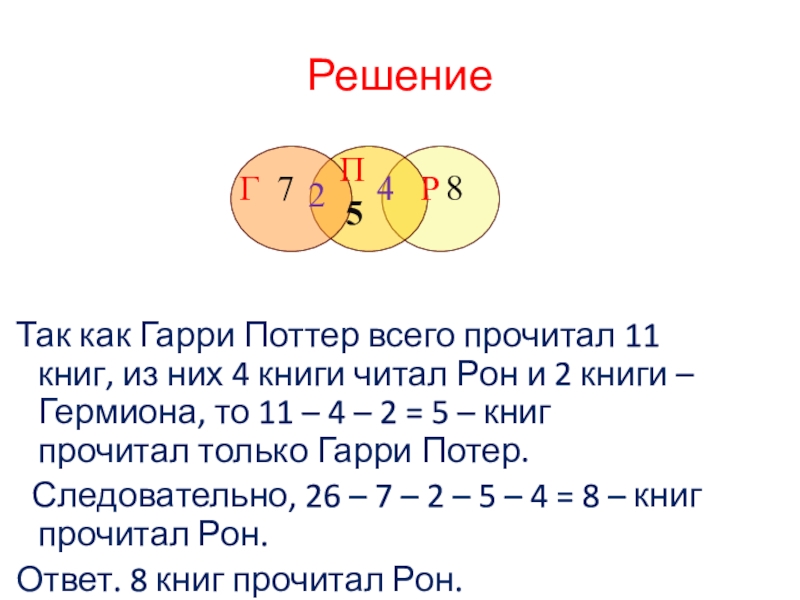
Слайд 10Задача №3 .
На полке стояло 26 волшебных книг по
Слайд 11Решение
Так как Гарри Поттер всего прочитал 11 книг, из них
Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.
Ответ. 8 книг прочитал Рон.
Г 7
П
Р
2
4
5
8
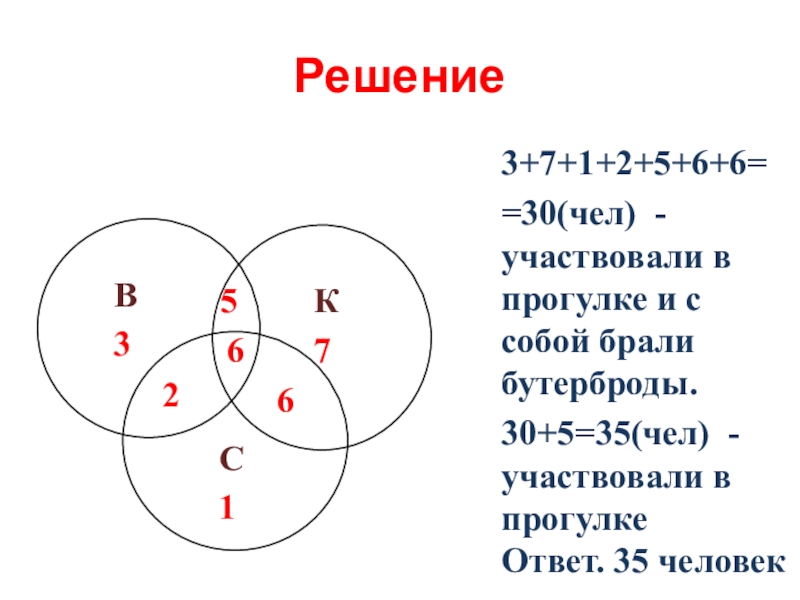
Слайд 12Задача №4 .
Сколько человек участвует в прогулке, если известно, что
Слайд 13Решение
3+7+1+2+5+6+6=
=30(чел) - участвовали в прогулке и с собой брали бутерброды.
30+5=35(чел)
В
3
К
7
С
1
6
2
5
6
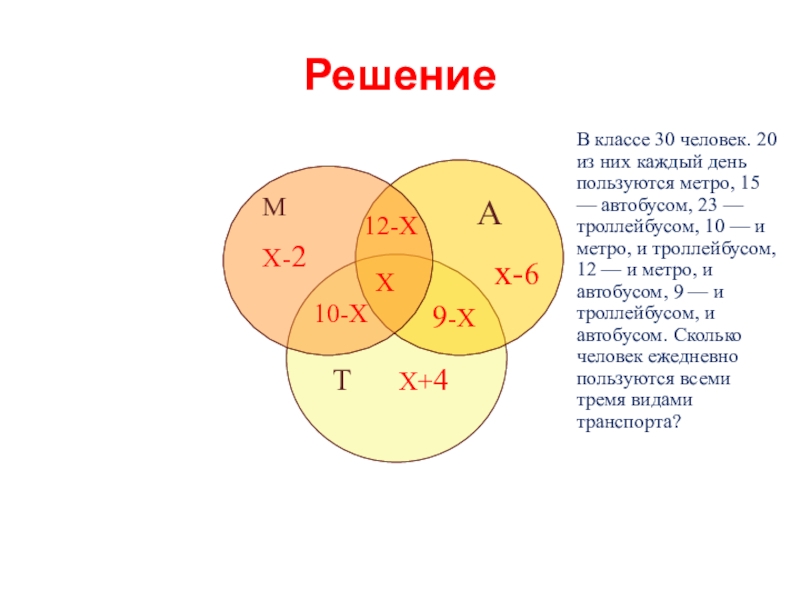
Слайд 14Задача №5.
В классе 30 человек. 20 из них
Слайд 15Решение
М
Х-2
А
х-6
12-Х
Х
10-Х
9-Х
Т Х+4
В классе 30 человек. 20 из
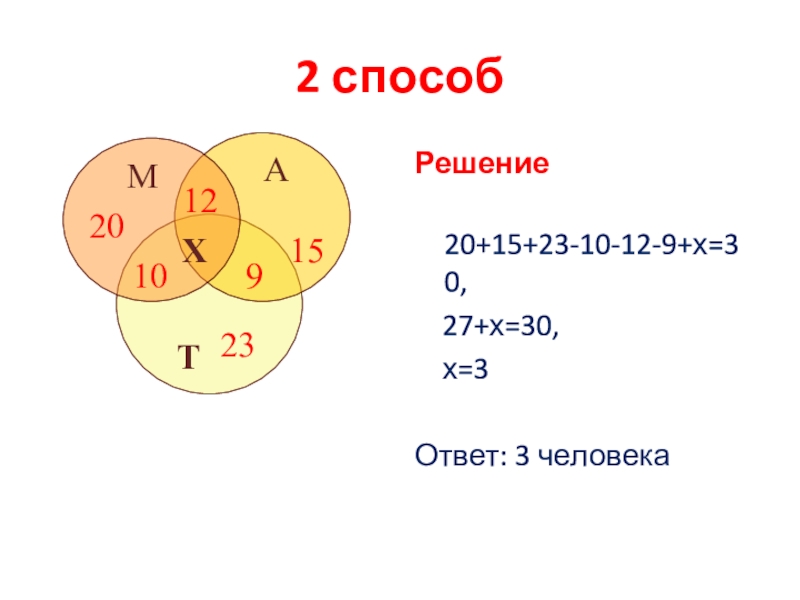
Слайд 16Решение
Пусть х человек пользуется всеми тремя видами транспорта. Тогда
20 − ((12 − х) + (10 − х) +х) = х − 2
Аналогично получаем: х − 6 — только автобусом и
х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.
отсюда х = 3.
Ответ: 3 человека.
Слайд 18Заключение
В моей работе рассмотрены задачи, которые состоят из большого
Данная тема расширила мой математический кругозор, обогатила арсенал средств, используемых в решении разнообразных задач.
Слайд 19Список используемой литературы:
1. Гаврилова Т. Д..Занимательная математика. 5 - 11 классы.
2. Германович П.Ю. «Сборник задач по математике на сообразительность».
3. Гетманова А. Д. Логические основы математики 10 – 11 класс: учебное пособие. – М.: Дрофа, 2005.
4. Глейзер Г. И. История математики в школе — М.:Просвещение, 1964. — С. 232.
5. Гусев В.А., Орлов А.И., Розенталь А.Л. «Внеклассная работа по математике». М.: Просвещение, 1984.
6. Нелин Е.П., Долгова О.Е.. Учебник алгебра и начала анализа 11 класс.