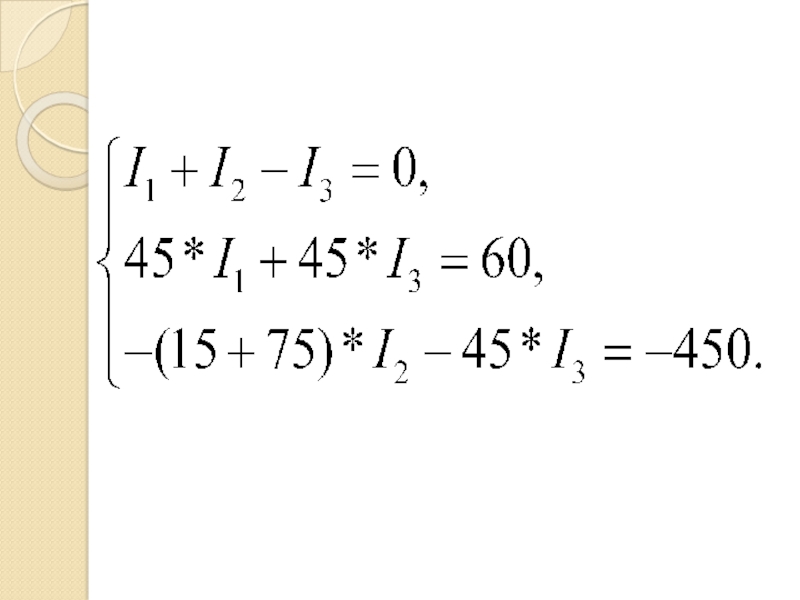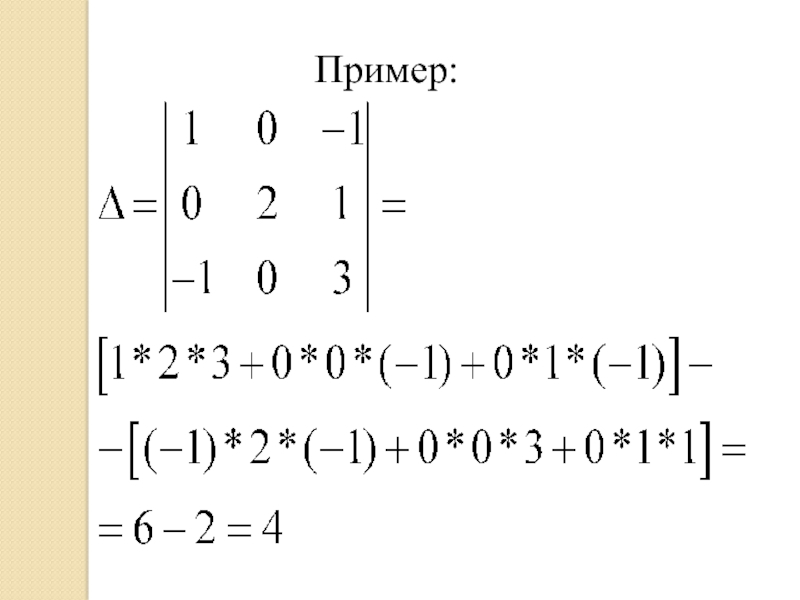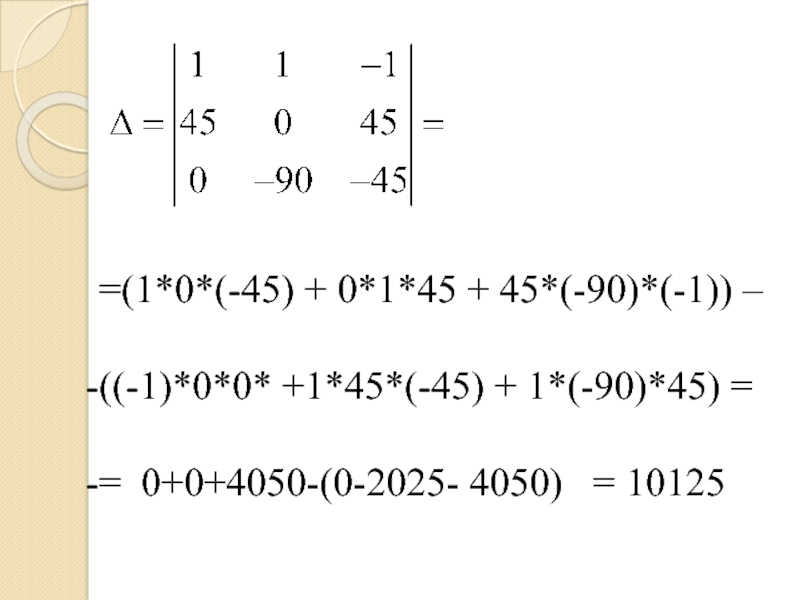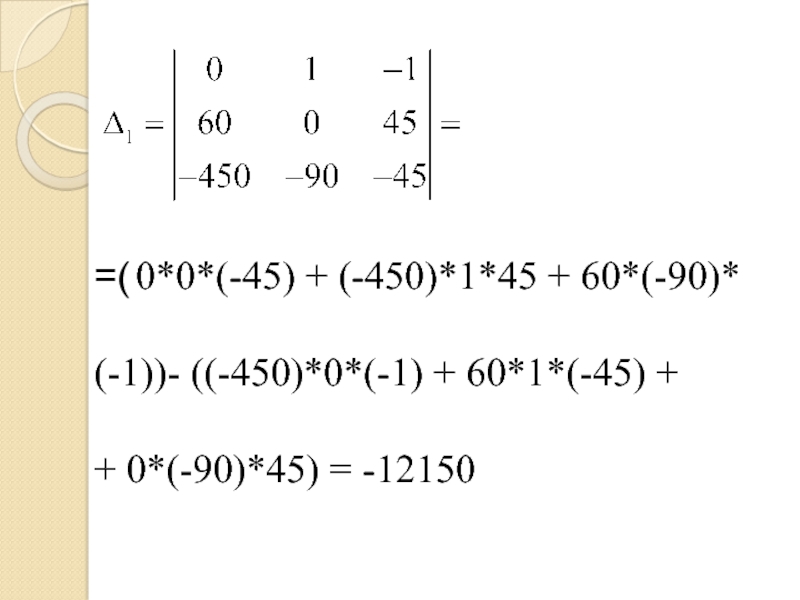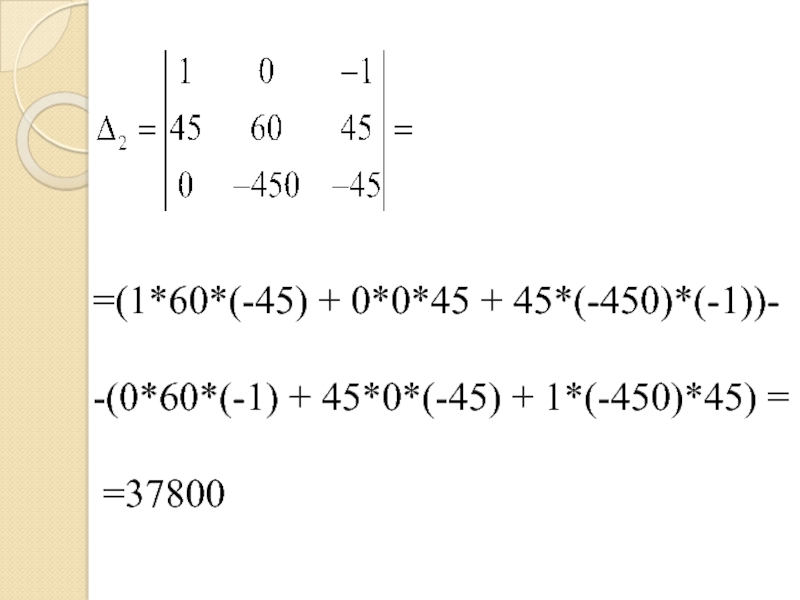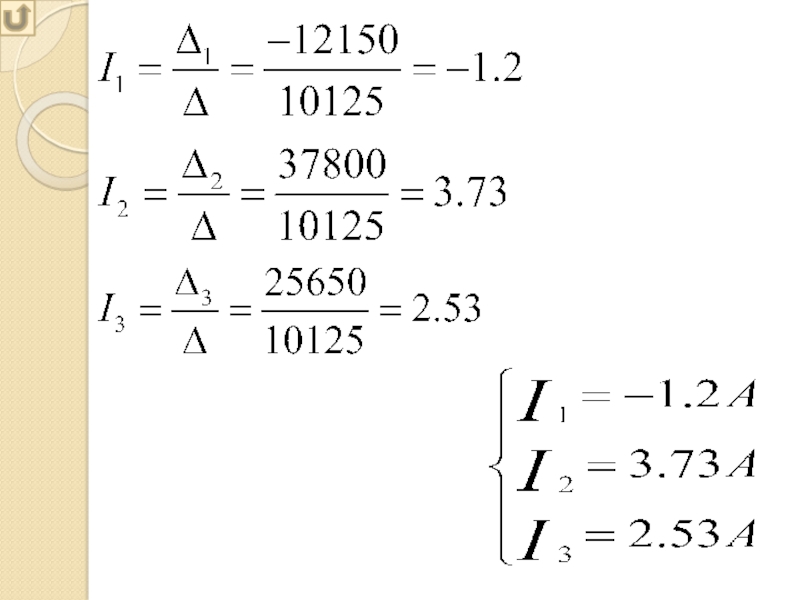- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение электротехнических задач методом моделирования
Содержание
- 1. Решение электротехнических задач методом моделирования
- 2. Задача:Закрепить применение законов Кирхгофа для электрической цепиПрименить
- 3. Цель занятия:Создать модель решения электротехнической задачи
- 4. Моделирование--метод познания, состоящий в создании и исследовании моделей
- 5. Модель-новый объект, который отражает существенные свойства изучаемого объекта и заменяющий его во время исследований.
- 6. Этапы разработки и исследования моделейОписательная информационная модель
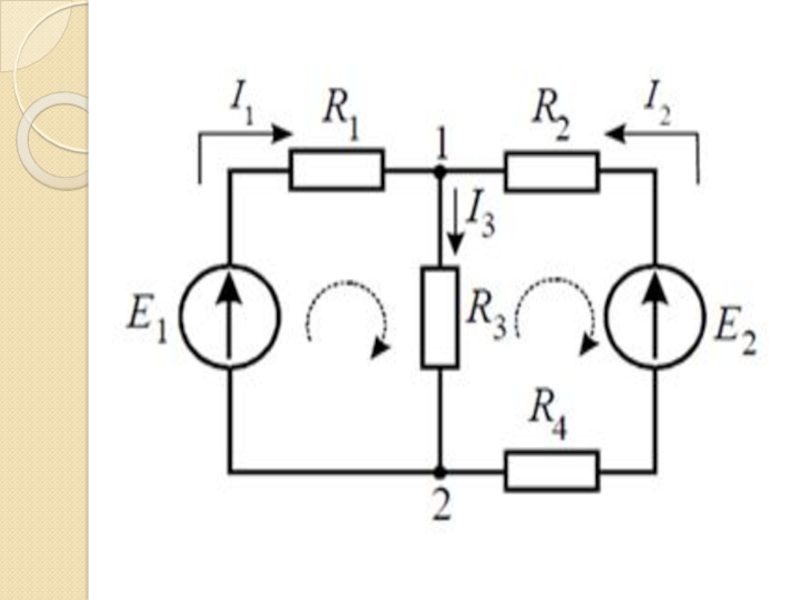
- 7. 1.Описательная информационная модель (постановка задачи)
- 8. Слайд 8
- 9. Густав Кирхгоф 1845 г.
- 10. 1 закон Кирхгофа Алгебраическая сумма токов в ветвях, сходящаяся в одном узле равна нулю
- 11. 2 закон Кирхгофа Алгебраическая сумма ЭДС, действующих
- 12. 2. Формальная модель (Построение математической модели)
- 13. Слайд 13
- 14. установил и опубликовал 1750 правило решения
- 15. Метод Крамера (Крамера правило) — способ решения
- 16. Система из m линейных уравнений с
- 17. Для системы n линейных уравнений с n неизвестнымис определителем матрицы системы Δ, отличным от нуля,
- 18. решение записывается в виде: где столбец матрицы системы заменяется столбцом свободных членов.
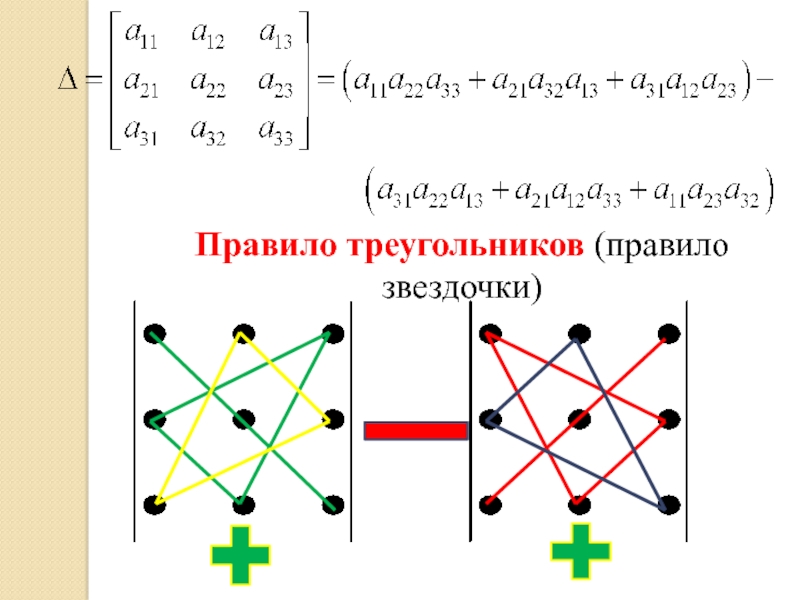
- 19. Слайд 19
- 20. Пример:
- 21. Найти решение системы уравнений:
- 22. Решение:
- 23. =(1*0*(-45) + 0*1*45 + 45*(-90)*(-1)) – ((-1)*0*0* +1*45*(-45) + 1*(-90)*45) == 0+0+4050-(0-2025- 4050) = 10125
- 24. =( 0*0*(-45) + (-450)*1*45 + 60*(-90)*(-1))- ((-450)*0*(-1) + 60*1*(-45) ++ 0*(-90)*45) = -12150
- 25. =(1*60*(-45) + 0*0*45 + 45*(-450)*(-1))--(0*60*(-1) + 45*0*(-45) + 1*(-450)*45) = =37800
- 26. = (1*0*(-450) + 0*1*60 + 45*(-90)*0)-(0*0*0 + 45*1*(-450) + 1*(-90)*60) = =25650
- 27. Слайд 27
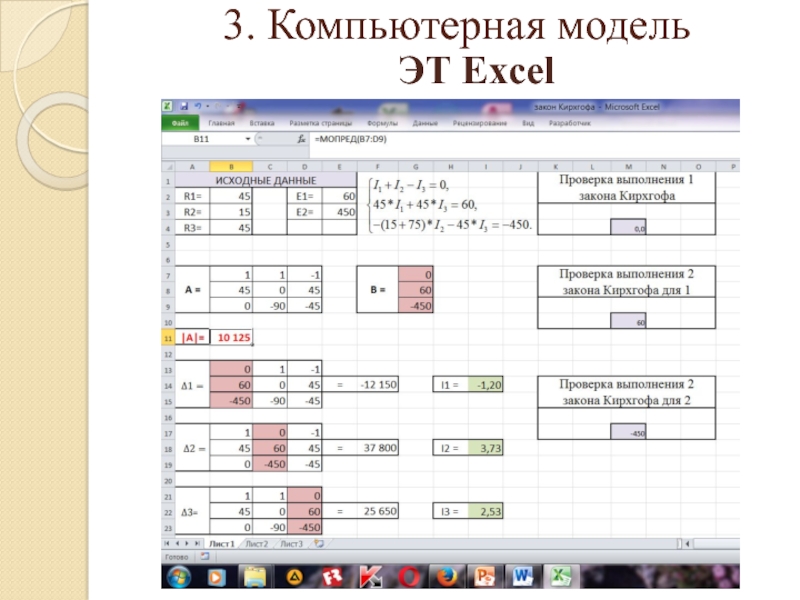
- 28. 3. Компьютерная модельЭТ Excel
- 29. =МОПРЕД (числовой массив) - вычисляет определитель матрицы(матрица хранится в числовом массиве)Формулы / Библиотека функций/ Математические
Задача:Закрепить применение законов Кирхгофа для электрической цепиПрименить метода Крамера для решения систем линейных уравненийАвтоматизировать расчеты в ЭТ ExcelВизуализировать модель электрической цепи
Слайд 1
Интегрированное учебное занятие
Тема: Решение электротехнических задач методом моделирования
Слайд 2Задача:
Закрепить применение законов Кирхгофа для электрической цепи
Применить метода Крамера для решения
систем линейных уравнений
Автоматизировать расчеты в ЭТ Excel
Визуализировать модель электрической цепи
Автоматизировать расчеты в ЭТ Excel
Визуализировать модель электрической цепи
Слайд 5Модель-
новый объект, который отражает существенные свойства изучаемого объекта и заменяющий его
во время исследований.
Слайд 6Этапы разработки и исследования моделей
Описательная информационная модель (постановка задачи)
Формальная модель
(Построение математической модели)
Компьютерная модель.
Компьютерный эксперимент и анализ полученных результатов.
Визуализация формальной модели.
Компьютерная модель.
Компьютерный эксперимент и анализ полученных результатов.
Визуализация формальной модели.
Слайд 112 закон Кирхгофа
Алгебраическая сумма ЭДС, действующих в любом контуре разветвленной электрической
цепи, равна алгебраической сумме падения напряжения на всех активных сопротивлениях этого контура
Слайд 14 установил и опубликовал 1750 правило решения систем линейных уравнений с
буквенными коэффициентам
заложил основы теории определителей
заложил основы теории определителей
Габриель Крамер, 1704-1752
Слайд 15 Метод Крамера
(Крамера правило)
— способ решения квадратных систем линейных алгебраических
уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Создан Габриелем Крамером в 1750 году.
Слайд 16
Система из m линейных уравнений с n неизвестными имеет вид:
a11 x1
+ a12 x2 +... + a1n xn = b1,
a21 x1 + a22 x2 +... + a2n xn = b2, ... ... ... ...
am1 x1 + am2 x2 +... + amn xn = bm.
аij (i =1..m ; j =1..n ) – заданные коэффициенты системы
bi – свободные члены системы
xj - неизвестные действительные числа
a21 x1 + a22 x2 +... + a2n xn = b2, ... ... ... ...
am1 x1 + am2 x2 +... + amn xn = bm.
аij (i =1..m ; j =1..n ) – заданные коэффициенты системы
bi – свободные члены системы
xj - неизвестные действительные числа
Слайд 17Для системы n линейных уравнений с n неизвестными
с определителем матрицы системы
Δ,
отличным от нуля,
отличным от нуля,
Слайд 18решение записывается в виде:
где
столбец матрицы системы заменяется
столбцом свободных членов.
Слайд 23=(1*0*(-45) + 0*1*45 + 45*(-90)*(-1)) –
((-1)*0*0* +1*45*(-45) + 1*(-90)*45) =
=
0+0+4050-(0-2025- 4050) = 10125
Слайд 24=( 0*0*(-45) + (-450)*1*45 + 60*(-90)*
(-1))- ((-450)*0*(-1) + 60*1*(-45) +
+ 0*(-90)*45)
= -12150
Слайд 29=МОПРЕД (числовой массив)
- вычисляет определитель матрицы
(матрица хранится в числовом массиве)
Формулы
/ Библиотека функций/ Математические