- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Расстояние между скрещивающимися прямыми.
Содержание
- 1. Расстояние между скрещивающимися прямыми.
- 2. Тема: Определение расстояния между скрещивающимися прямымиЦель урока:
- 3. Определение: Скрещивающимися называются прямые , лежащие в разных плоскостях.Примеры скрещивающихся прямых в окружающей среде
- 4. Определение 1: Расстоянием между двумя скрещивающимися прямыми
- 5. Существует три способа определения расстояния между скрещивающимися
- 6. Расстояние между скрещивающимися прямыми равно
- 7. 2-ой способРасстояние между скрещивающимися прямыми равно длине
- 8. Расстояние между скрещивающимися прямыми равно
- 9. Дано: прямая а параллельна плоскости α (
Слайд 2Тема: Определение расстояния между скрещивающимися прямыми
Цель урока: Научить определять расстояние между
Задачи урока:
Обучающие:
-Дать определение скрещивающихся прямых
-Научить строить общий перпендикуляр для двух скрещивающихся прямых
Развивающие:
-Продолжить дальнейшее формирование пространственного воображения
-Развивать аналитическое мышление
Воспитательные:
-Усилить мотивацию изучения геометрии
-Воспитывать умение достигать поставленной цели.
Слайд 3Определение: Скрещивающимися называются прямые , лежащие в разных плоскостях.
Примеры скрещивающихся прямых
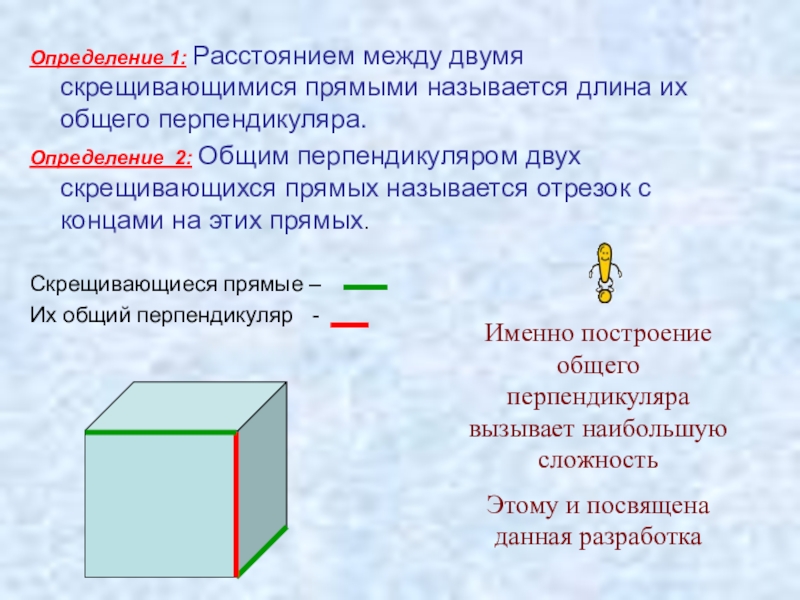
Слайд 4Определение 1: Расстоянием между двумя скрещивающимися прямыми называется длина их общего
Определение 2: Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых.
Скрещивающиеся прямые –
Их общий перпендикуляр -
Именно построение общего перпендикуляра вызывает наибольшую сложность
Этому и посвящена данная разработка
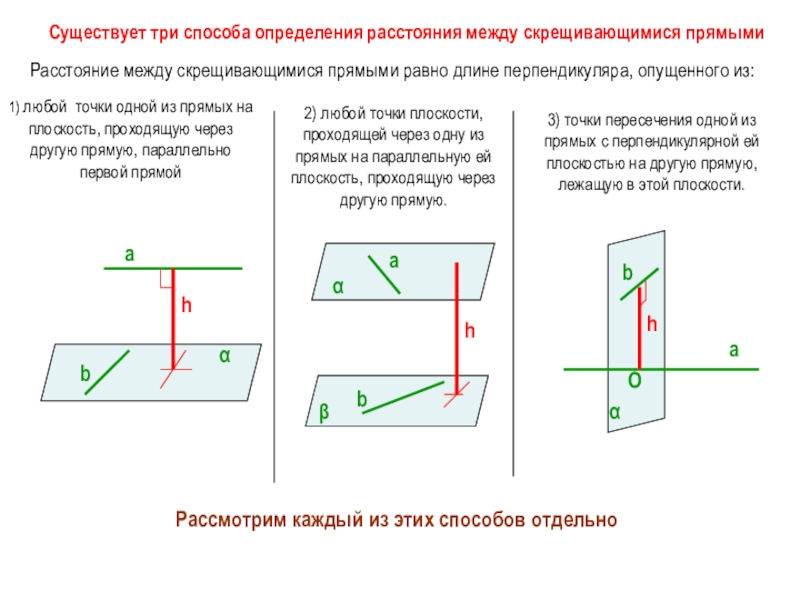
Слайд 5Существует три способа определения расстояния между скрещивающимися прямыми
Расстояние между скрещивающимися
1) любой точки одной из прямых на плоскость, проходящую через другую прямую, параллельно первой прямой
а
b
α
h
2) любой точки плоскости, проходящей через одну из прямых на параллельную ей плоскость, проходящую через другую прямую.
b
а
α
β
h
3) точки пересечения одной из прямых с перпендикулярной ей плоскостью на другую прямую, лежащую в этой плоскости.
h
a
b
α
O
Рассмотрим каждый из этих способов отдельно
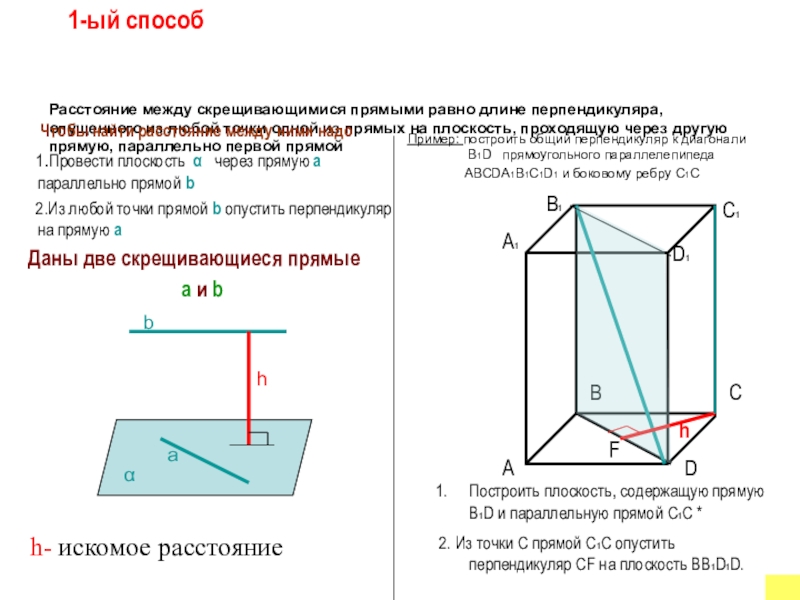
Слайд 6 Расстояние между скрещивающимися прямыми равно длине перпендикуляра, опущенного из любой точки
Чтобы найти расстояние между ними надо:
1.Провести плоскость α через прямую а параллельно прямой b
2.Из любой точки прямой b опустить перпендикуляр на прямую а
Даны две скрещивающиеся прямые
а и b
Пример: построить общий перпендикуляр к диагонали В1D прямоугольного параллелепипеда
ABCDA1B1C1D1 и боковому ребру С1С
b
a
h
α
h- искомое расстояние
А
В
С
D
A1
B1
C1
D1
F
Построить плоскость, содержащую прямую В1D и параллельную прямой С1С *
2. Из точки С прямой С1С опустить перпендикуляр СF на плоскость ВВ1D1D.
1-ый способ
h
Слайд 7
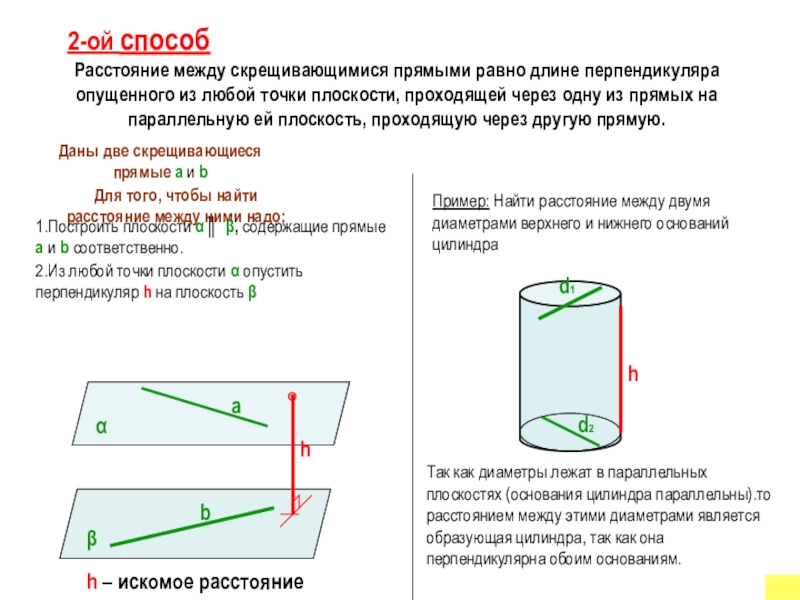
2-ой способ
Расстояние между скрещивающимися прямыми равно длине перпендикуляра опущенного из любой
Даны две скрещивающиеся прямые а и b
α
β
а
b
h
Для того, чтобы найти расстояние между ними надо:
1.Построить плоскости α ║ β, содержащие прямые а и b соответственно.
2.Из любой точки плоскости α опустить перпендикуляр h на плоскость β
Пример: Найти расстояние между двумя диаметрами верхнего и нижнего оснований цилиндра
h
Так как диаметры лежат в параллельных плоскостях (основания цилиндра параллельны).то расстоянием между этими диаметрами является образующая цилиндра, так как она перпендикулярна обоим основаниям.
d1
d2
h – искомое расстояние
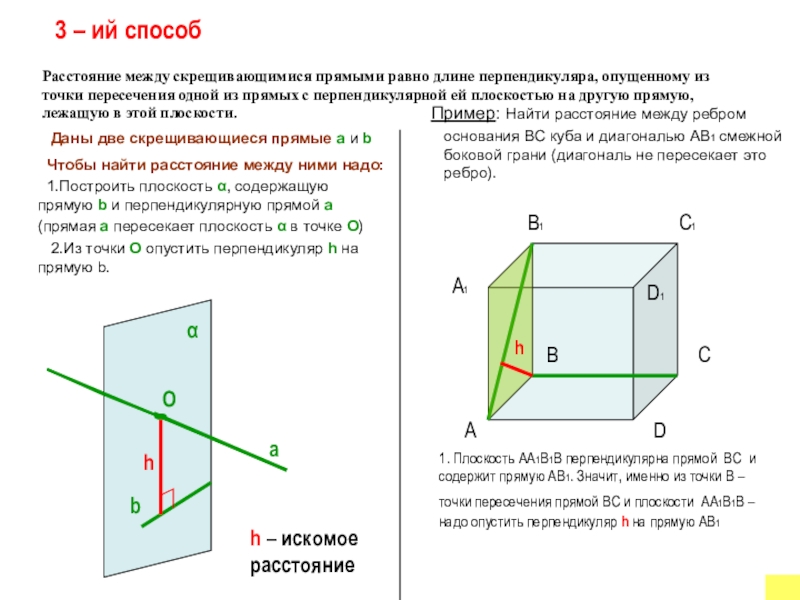
Слайд 8 Расстояние между скрещивающимися прямыми равно длине перпендикуляра, опущенному из точки пересечения
Даны две скрещивающиеся прямые а и b
Чтобы найти расстояние между ними надо:
1.Построить плоскость α, содержащую прямую b и перпендикулярную прямой а
(прямая а пересекает плоскость α в точке О)
2.Из точки О опустить перпендикуляр h на прямую b.
Пример: Найти расстояние между ребром основания ВС куба и диагональю АВ1 смежной боковой грани (диагональ не пересекает это ребро).
а
b
О
α
h
h – искомое расстояние
3 – ий способ
В1
С1
D1
A1
B
C
D
A
1. Плоскость АА1В1В перпендикулярна прямой ВС и содержит прямую АВ1. Значит, именно из точки В – точки пересечения прямой ВС и плоскости АА1В1В – надо опустить перпендикуляр h на прямую АВ1
h
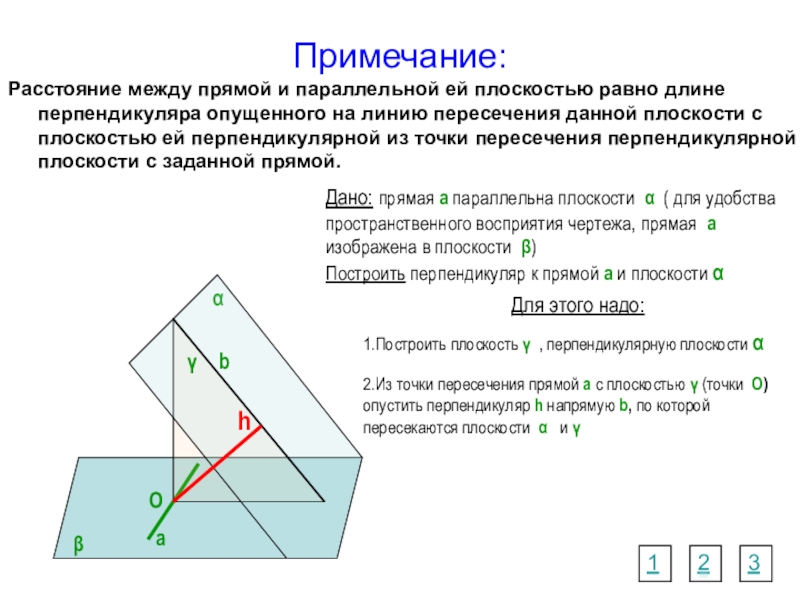
Слайд 9Дано: прямая а параллельна плоскости α ( для удобства пространственного восприятия
Примечание:
Расстояние между прямой и параллельной ей плоскостью равно длине перпендикуляра опущенного на линию пересечения данной плоскости с плоскостью ей перпендикулярной из точки пересечения перпендикулярной плоскости с заданной прямой.
β
α
a
Для этого надo:
1.Построить плоскость γ , перпендикулярную плоскости α
2.Из точки пересечения прямой а с плоскостью γ (точки О) опустить перпендикуляр h напрямую b, по которой пересекаются плоскости α и γ
b
О
γ
h
1
2
3