- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Теоремы теории вероятностей
Содержание
- 1. Презентация Теоремы теории вероятностей
- 2. Теорема сложения вероятностей несовместных событий:Вероятность появления одного
- 3. Теорема сложения вероятностей совместный событий:Вероятность появления хотя
- 4. Теорема умножения вероятностей независимых событий: Вероятность совместного
- 5. Теорема умножения вероятностей зависимых событий: Вероятность совместного
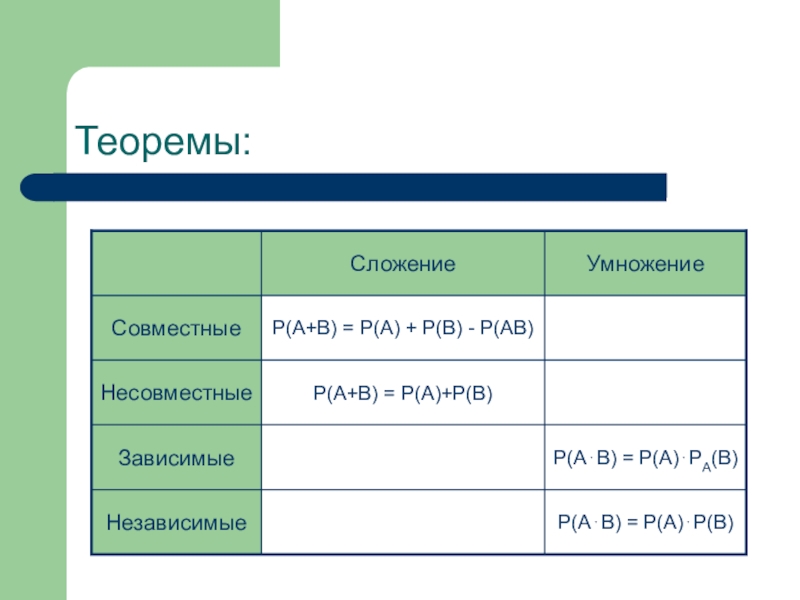
- 6. Теоремы:
- 7. Пример 1. Стрелок стреляет по мишени, разделенной
- 8. План решения задачиОбозначить события буквами. А - стрелок
- 9. Пример 2. Разрыв электрической цепи происходит в
- 10. Пример 3.У сборщика имеется 3 конусных и
- 11. Пример 4.Вероятности попадания в цель при стрельбе
- 12. Задание:Вероятность того, что стрелок попадет в мишень
- 13. а) все 3 выстрела попали в цель;
- 14. а) все 3 выстрела попали в цель;
Слайд 2Теорема сложения вероятностей несовместных событий:
Вероятность появления одного из двух несовместных событий
P(A+B) = P(A)+P(B)
Слайд 3Теорема сложения вероятностей совместный событий:
Вероятность появления хотя бы одного из двух
P(A+B) = P(A) + P(B) - P(AB)
Слайд 4Теорема умножения вероятностей независимых событий:
Вероятность совместного появления двух независимых событий
P(A⋅B) = P(A)⋅P(B)
Слайд 5Теорема умножения вероятностей зависимых событий:
Вероятность совместного появления двух зависимых событий
P(A⋅B) = P(A)⋅PA(B)
Слайд 7Пример 1.
Стрелок стреляет по мишени, разделенной на 3 непересекающиеся области.
Найти вероятность того, что стрелок при одном выстреле попадет в первую или во вторую области.
Решение:
А - стрелок попал в первую область, Р(А) = 0,45;
В - стрелок попал во вторую область, Р(В) = 0,35;
А + В – (стрелок попал либо в первую), или (во вторую область).
События А и В несовместны (попадание в одну область исключает попадание в другую).
Искомая вероятность: Р(А + В) = Р(А) + Р(В) = 0,45 + 0,35 = 0,8.
Слайд 8План решения задачи
Обозначить события буквами.
А - стрелок попал в первую область,
В
Определить вероятность событий из п.1.
Р(А) = 0,45 Р(В) = 0,35
Записать в виде формулы событие, вероятность которого нужно найти.
А + В – (стрелок попал либо в первую), или (во вторую область)
Записать формулу для вычисления вероятности события из п. 3.
Р(А + В) = Р(А) + Р(В)
Вычислить искомую вероятность.
Р(А + В) = Р(А) + Р(В) = 0,45 + 0,35 = 0,8
Слайд 9Пример 2.
Разрыв электрической цепи происходит в том случае, когда выходит
Определить вероятность того, что не будет разрыва цепи, если элементы выходят из строя с вероятностями 0,3; 0,4 и 0,6.
Решение:
А - первый элемент не выйдет из строя, Р(А) = 1 - 0,3;
В - второй элемент не выйдет из строя, Р(В) = 1 - 0,4;
С - третий элемент не выйдет из строя, Р(С) = 1 - 0,6.
А⋅В⋅С - не будет разрыва цепи (не один элемент не выйдет из строя).
События А, В и С независимы, следовательно Р(А⋅В⋅С) = Р(А)⋅Р(В)⋅Р(С).
Р(А⋅В⋅С) = Р(А)⋅Р(В)⋅Р(С) = 0,7 ⋅ 0,6 ⋅ 0,4 = 0,168.
Слайд 10Пример 3.
У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик
Найти вероятность того, что первый из взятых валиков - конусный, а второй - эллиптический.
Решение:
А - первый валик - конусный, Р(А) = 3/10;
В - второй валик - эллиптический, РА(В) = 7/9 - вероятность события В, вычисленная в предположении, что произошло
событие А (т.е. первый валик был конусным).
A ⋅ B - первый валик - конусный, второй - эллиптический.
События А и В зависимые, поэтому:
P(A⋅B) = P(A) ⋅PA(B) = (3 / 10 ) ⋅ ( 7 / 9 )= 21 / 90 = 7 / 30.
Слайд 11Пример 4.
Вероятности попадания в цель при стрельбе из двух орудий соответственно
Решение:
А - попадание из первого орудия, Р(А) = 0,7;
В - попадание из второго орудия, Р(В) = 0,8;
А + В - попадание хотя бы из одного орудия. События А и В совместны.
Р(А+В) = P(A) + P(B) - P(A⋅B).
События А и В независимы, т.к. вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия.
Р(А⋅В) = Р(А) ⋅ Р(В) = 0,7 ⋅ 0,8 = 0,56.
Искомая вероятность: Р(А+В) = 0,7 + 0,8 - 0,56 = 0,94.
Слайд 12Задание:
Вероятность того, что стрелок попадет в мишень при одном выстреле равна
Найти вероятность того, что
а) все 3 выстрела попали в цель;
б) хотя бы один выстрел попал в цель;
в) ровно один выстрел попал в цель;
г) ровно два выстрела попали в цель;
д) ни один выстрел не попал в цель.
Слайд 13а) все 3 выстрела попали в цель; б) хотя бы один
а) (первый выстрел попал) и (второй выстрел попал) и (третий выстрел попал);
б) (первый выстрел попал) или (второй выстрел попал) или (третий выстрел попал);
в) [(первый попал) и (второй не попал) и (третий не попал)]
или
[(первый не попал) и (второй попал) и (третий не попал)]
или
[(первый не попал) и (второй не попал) и (третий попал)];
г) [(первый попал) и (второй попал) и (третий не попал)]
или
[(первый не попал) и (второй попал) и (третий попал)]
или
[(первый попал) и (второй не попал) и (третий попал)];
д) (первый выстрел не попал) и (второй выстрел не попал) и (третий выстрел не попал).
Слайд 14а) все 3 выстрела попали в цель; б) хотя бы один
а) A·A·A
б) A+A+A
в) A·A·A + A·A·A + A·A·A
г) A·A·A + A·A·A + A·A·A
д) A·A·A