- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение олимпиадных задач
Содержание
- 1. Презентация Решение олимпиадных задач
- 2. Задача 1(Школьный этап Всероссийской олимпиады в 2013/2014
- 3. D
- 4. Решение
- 5. Задача 2(Школьный этап Всероссийской олимпиады в 2013/2014
- 6. D
- 7. Решение
- 8. Задача 3( Районная олимпиада Ростовской области 2013/2014г.)
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Решение
- 13. Задача 4(Районная олимпиада Ростовской области 2013/2014г.) Найдите
- 14. Слайд 14
- 15. Решение
- 16. Слайд 16
- 17. Задача 5 Окружность, вписанная в прямоугольный треугольник
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Задача 6 Существуют ли в пространстве
- 22. Слайд 22
- 23. Слайд 23
- 24. Задача 7 Существует ли тетраэдр, все грани
- 25. Слайд 25
- 26. Слайд 26
- 27. Задача 8 Существует ли многогранник с нечетным
- 28. Задача 9 В равнобедренном треугольнике длины боковых
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Задача 10 На продолжениях сторон выпуклого четырехугольника
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
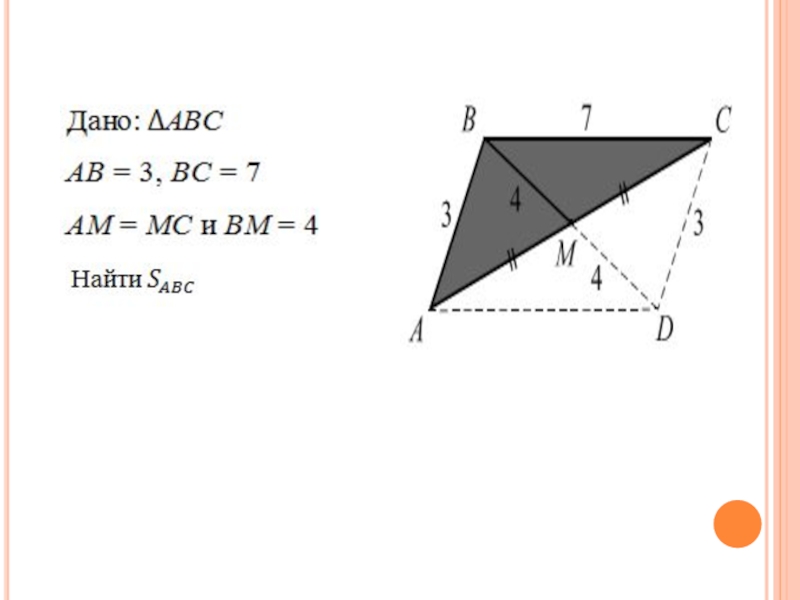
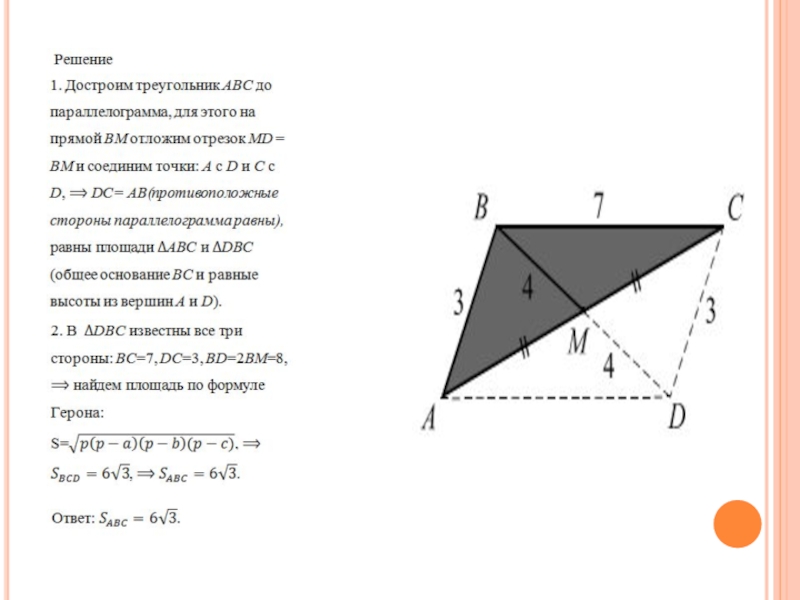
- 36. Задача 11 Найти площадь треугольника, две стороны
- 37. Слайд 37
- 38. Слайд 38
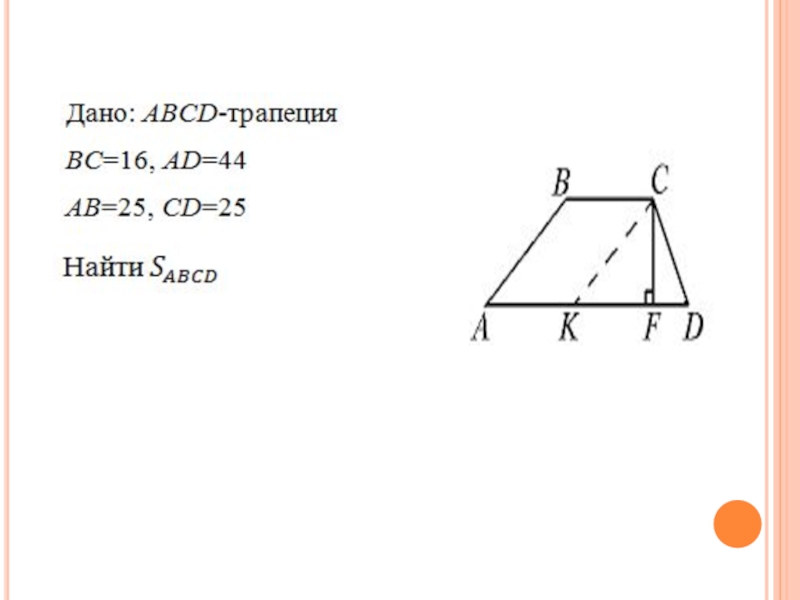
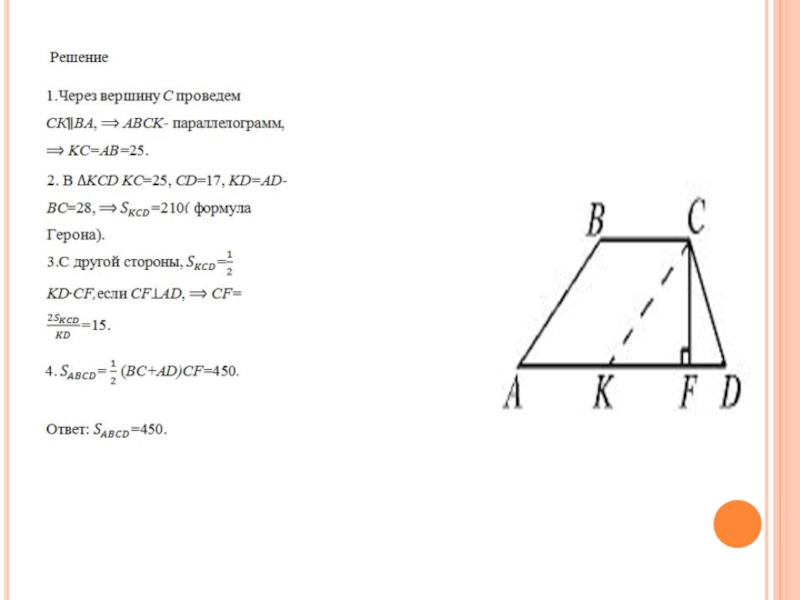
- 39. Задача 12 Найти площадь трапеции, если её
- 40. Слайд 40
- 41. Слайд 41
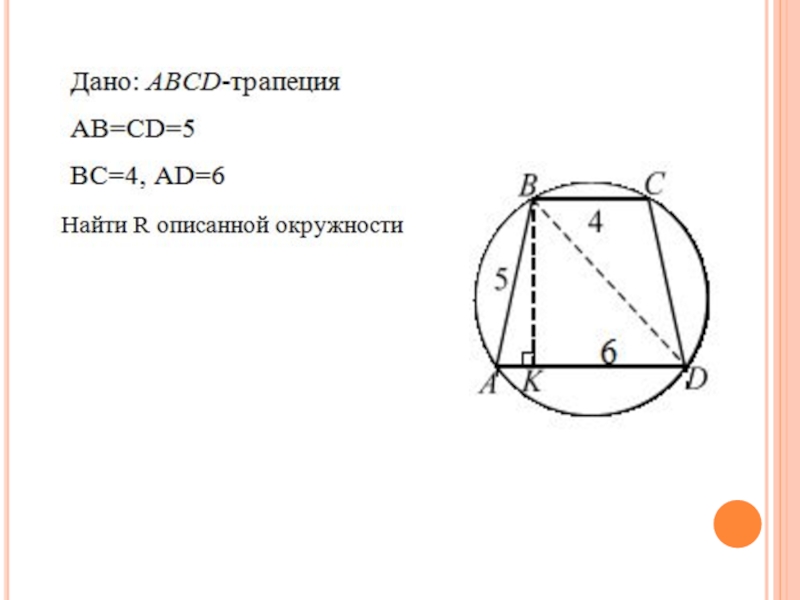
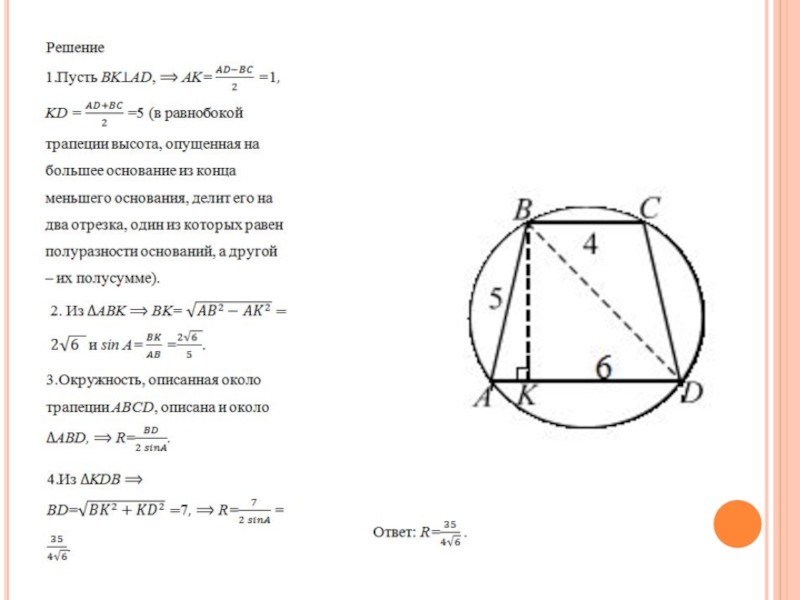
- 42. Задача 13 Основания равнобокой трапеции равны 4
- 43. Слайд 43
- 44. Слайд 44
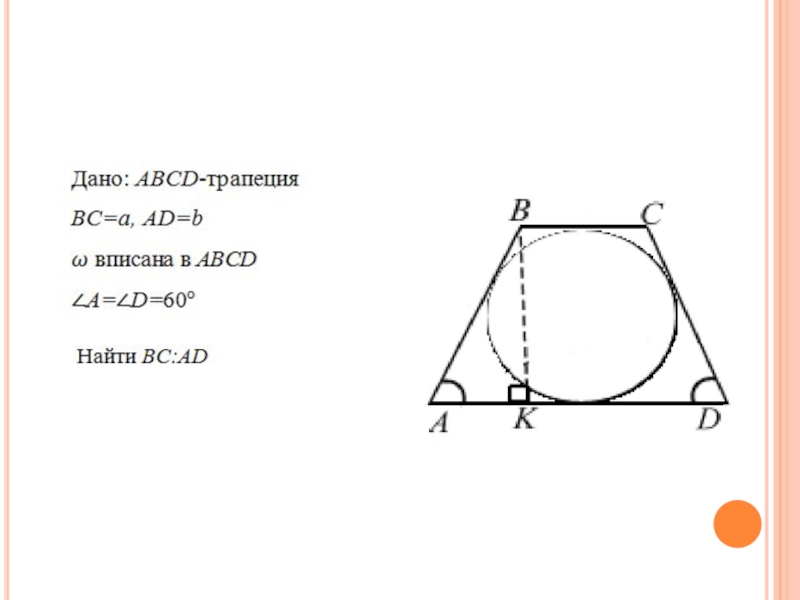
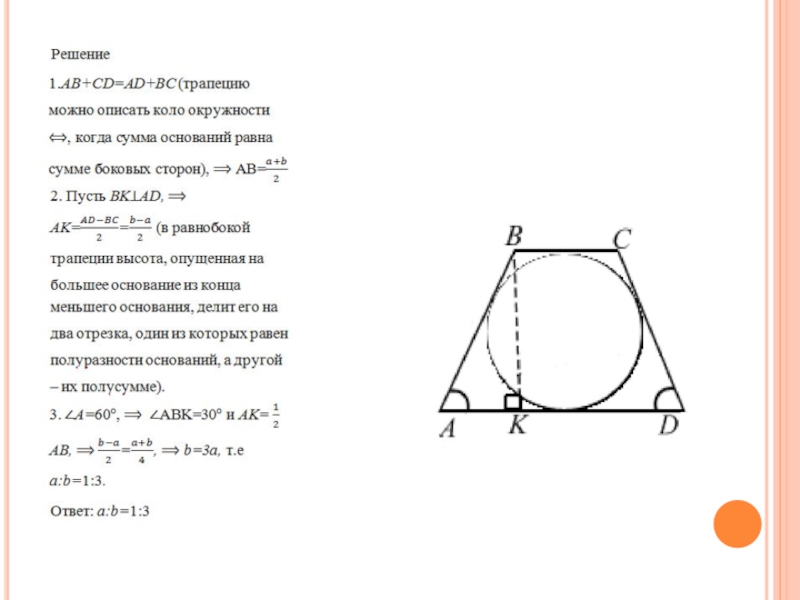
- 45. Задача 14 Около окружности описана равнобокая трапеция с острым углом 60. Найти отношение длин оснований.
- 46. Слайд 46
- 47. Слайд 47
- 48. Задача 15 В окружности радиуса 13 через
- 49. Слайд 49
- 50. Слайд 50
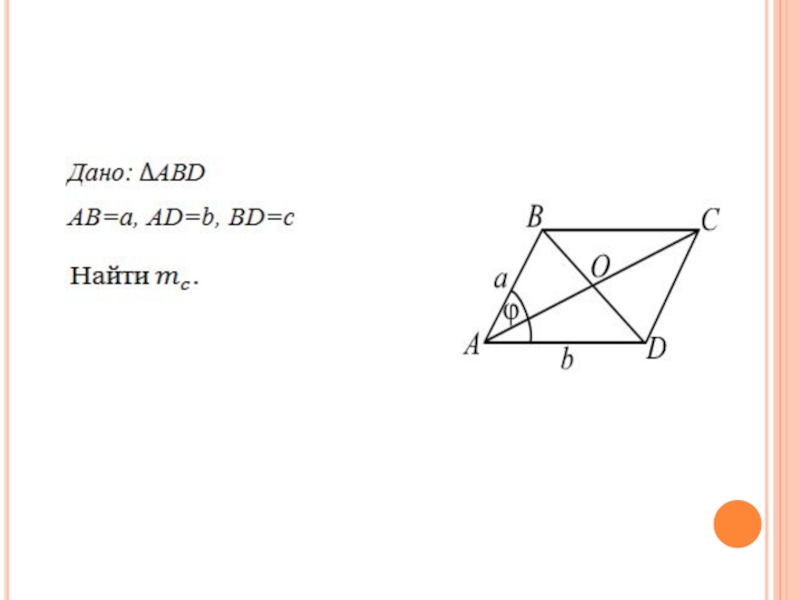
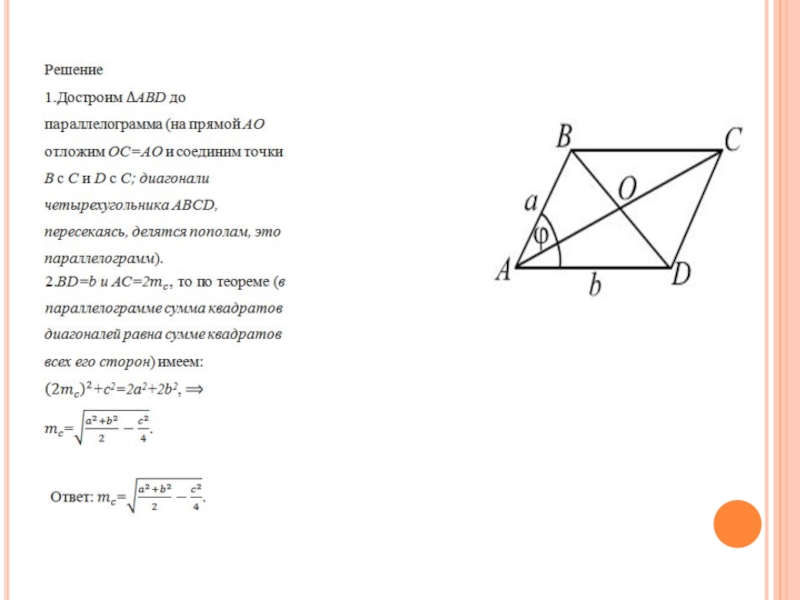
- 51. Задача 16 Зная три стороны треугольника a, b, c найти медиану к стороне c.
- 52. Слайд 52
- 53. Слайд 53
- 54. Задача 17 В треугольнике ABC точки M
- 55. Слайд 55
- 56. Слайд 56
- 57. Задача 18 Из одной точки окружности проведены
- 58. Слайд 58
- 59. Слайд 59
- 60. Задача 19
- 61. Слайд 61
- 62. Слайд 62
- 63. Задача 20 Около окружности радиуса 5 описан
- 64. Слайд 64
- 65. Слайд 65
- 66. Спасибо за внимание!
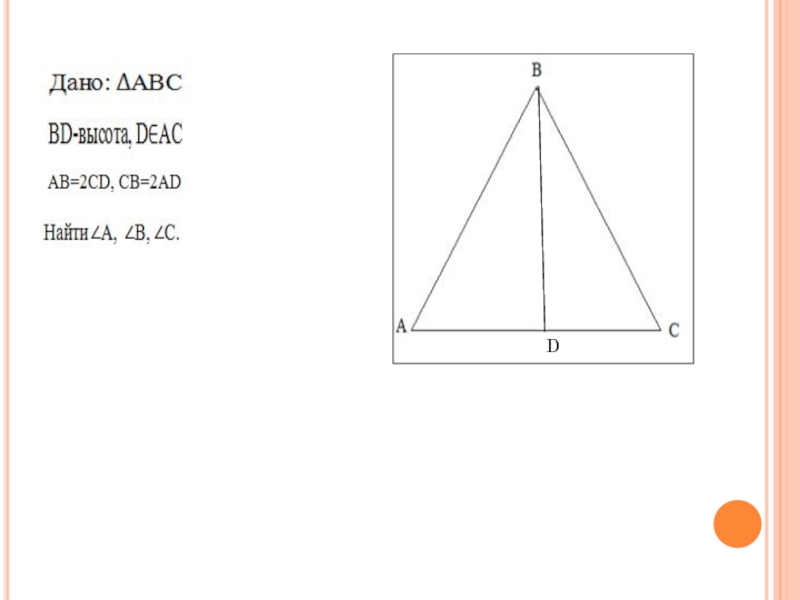
Задача 1(Школьный этап Всероссийской олимпиады в 2013/2014 г.) В треугольнике ABC проведена высота BD (точка D лежит на стороне AC). Оказалось, что, AB=2CD и CB=2AD. Найдите углы треугольника ABC.
Слайд 2Задача 1(Школьный этап Всероссийской олимпиады в 2013/2014 г.)
В треугольнике ABC проведена
высота BD (точка D лежит на стороне AC). Оказалось, что, AB=2CD и CB=2AD. Найдите углы треугольника ABC.
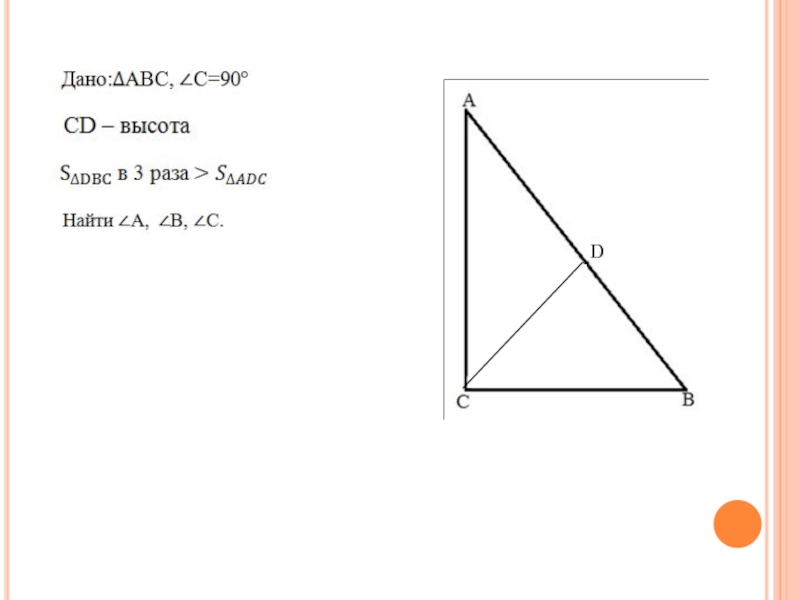
Слайд 5Задача 2(Школьный этап Всероссийской олимпиады в 2013/2014 г.)
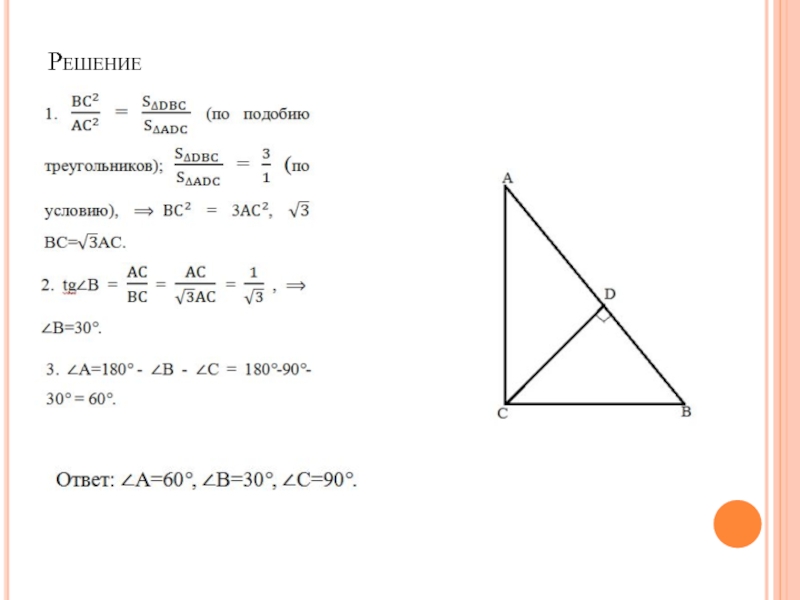
В прямоугольном треугольнике ABC
из вершины прямого угла проведена высота CD. Найдите углы треугольника ABC , если известно, что площадь треугольника DBC в 3 раза больше площади треугольника ADC.
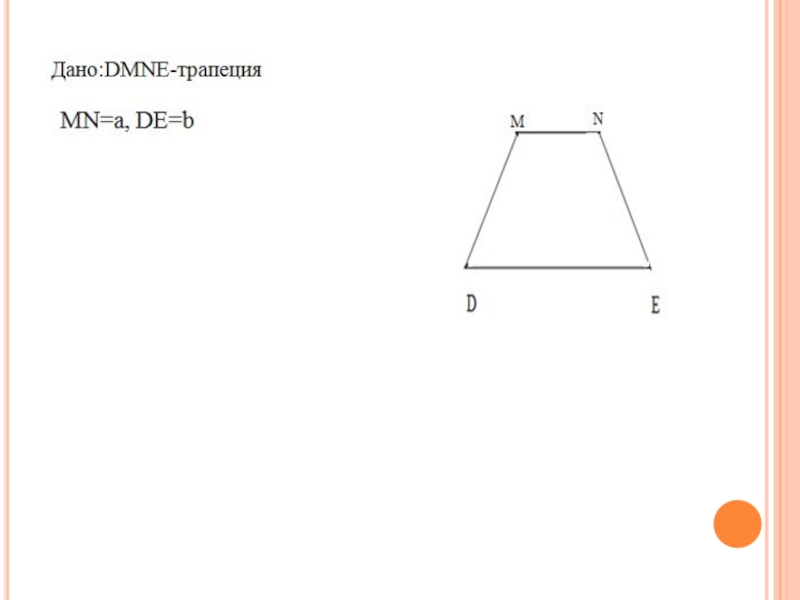
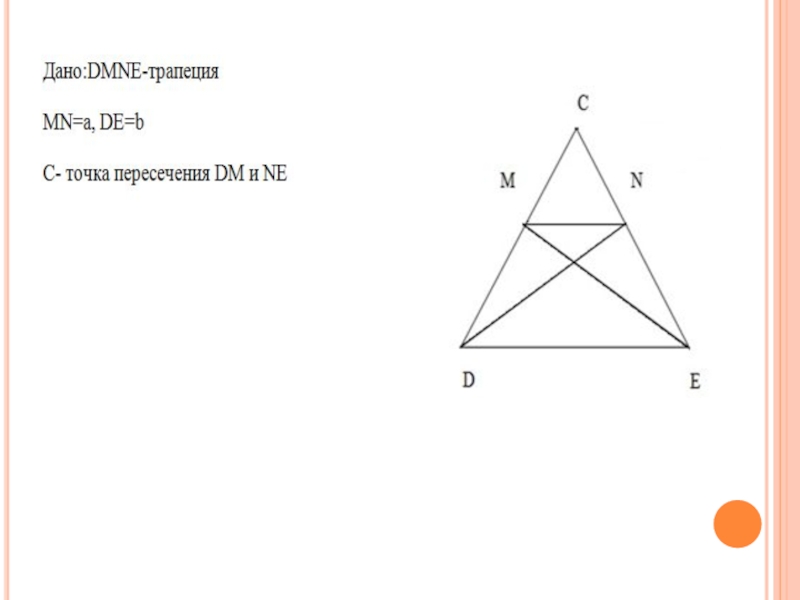
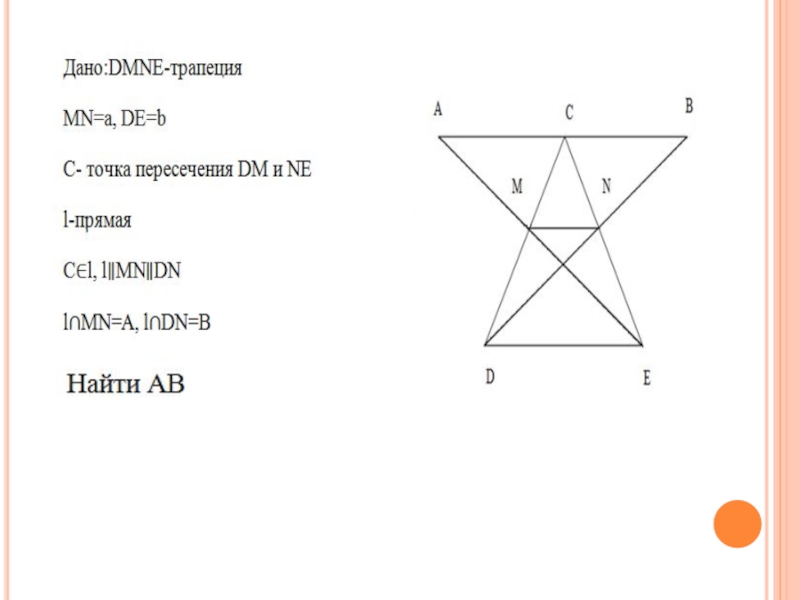
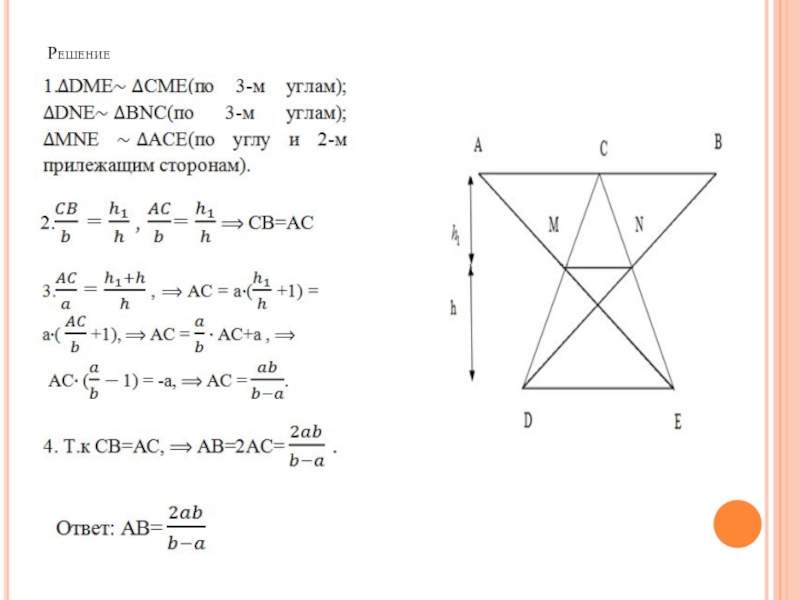
Слайд 8Задача 3( Районная олимпиада Ростовской области 2013/2014г.)
Непараллельные стороны трапеции продолжены до
взаимного пересечения и через полученную точку проведена прямая, параллельная основаниям трапецию. Найти отрезок её, ограниченный продолжениями диагоналей, если основания равны a и b (аb).
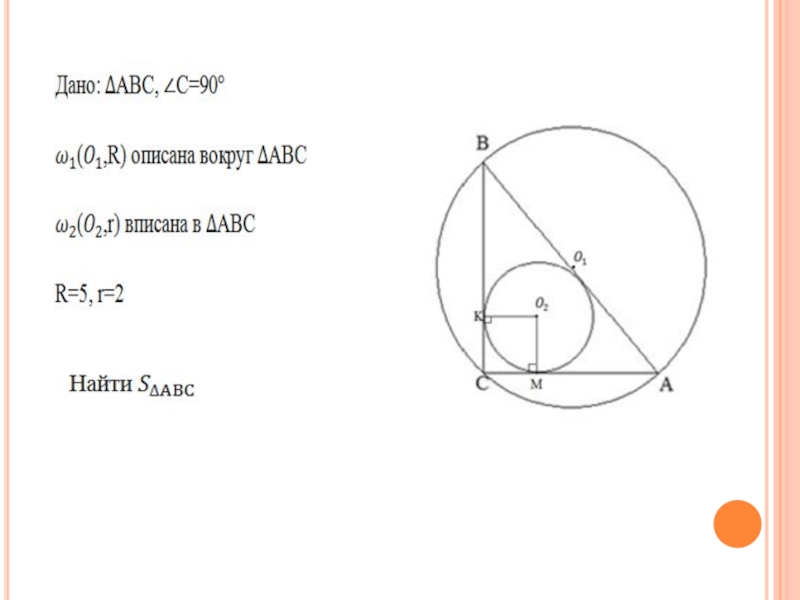
Слайд 13Задача 4(Районная олимпиада Ростовской области 2013/2014г.)
Найдите площадь прямоугольного треугольника, если радиус
описанной около него окружности равен 5, а радиус вписанной в него окружности равен 2.
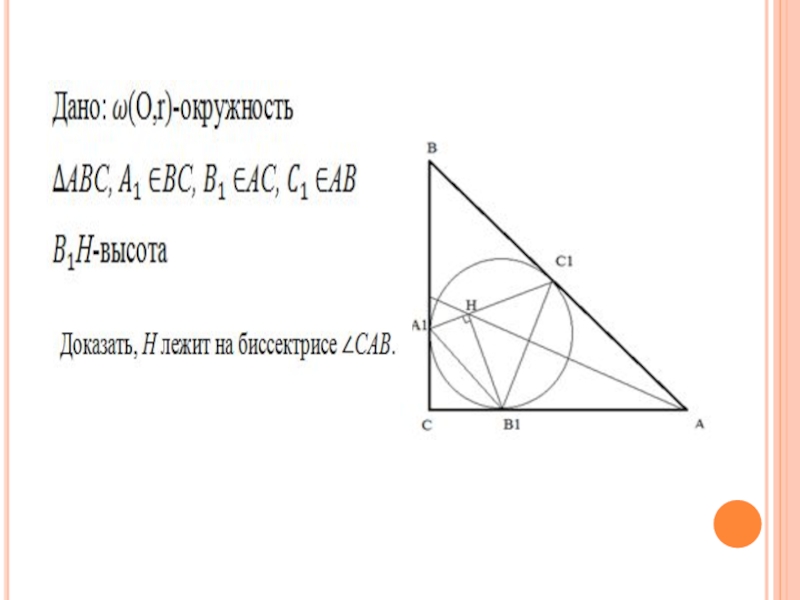
Слайд 17Задача 5
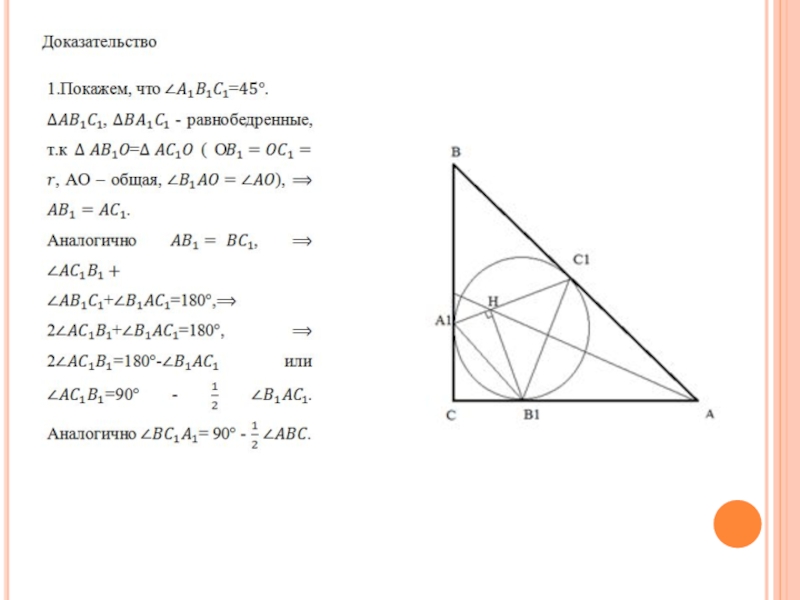
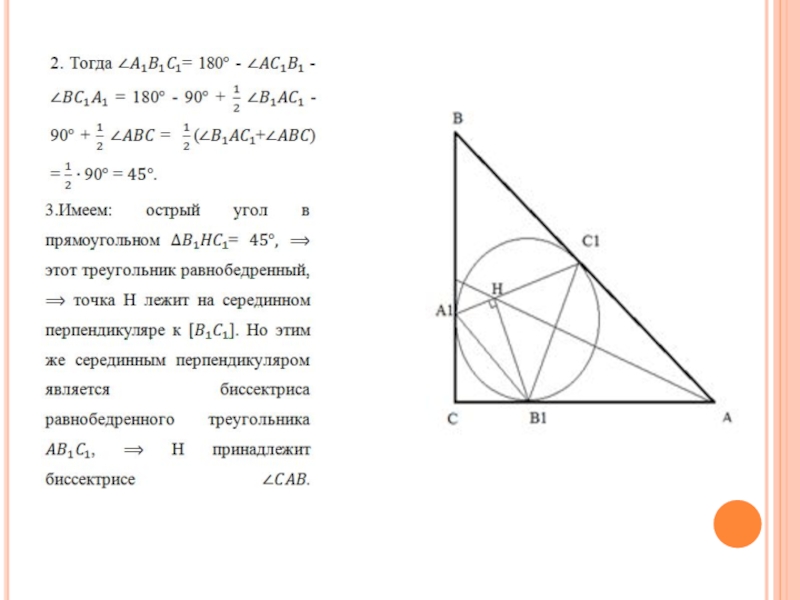
Окружность, вписанная в прямоугольный треугольник ABC с гипотенузой AB, касается
его сторон BC, AC, AB в точках , , соответственно. H-высота треугольника . Доказать, что точка H лежит на биссектрисе угла CAB.
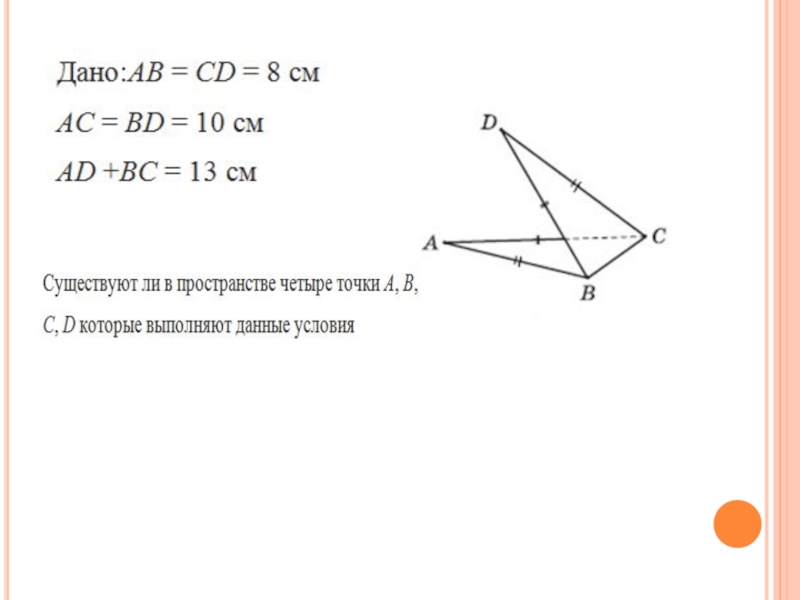
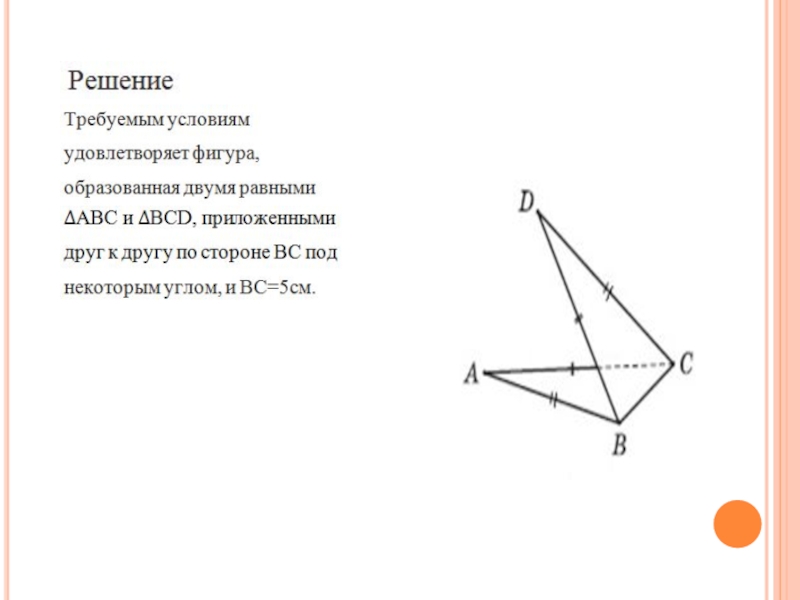
Слайд 21Задача 6
Существуют ли в пространстве четыре точки A, B, C,
D такие, что AB = CD = 8 см, AC = BD = 10 см, AD +BC = 13 см.
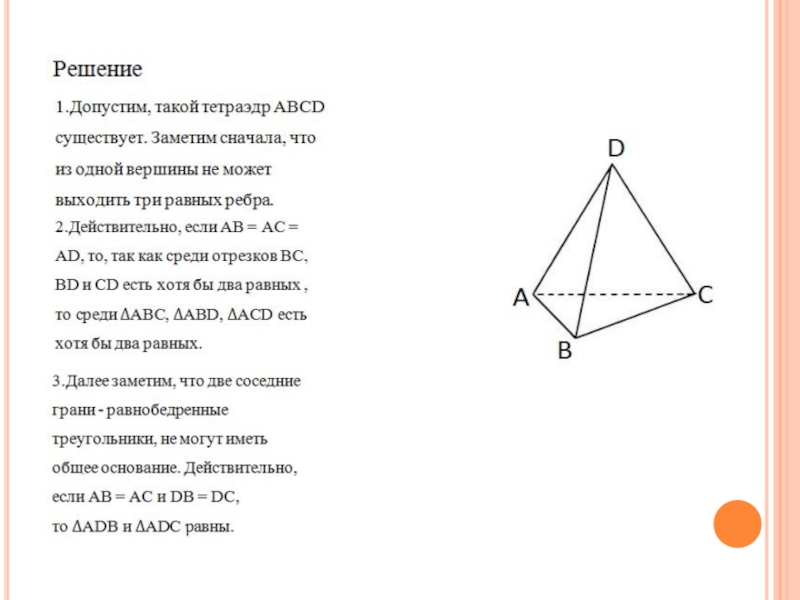
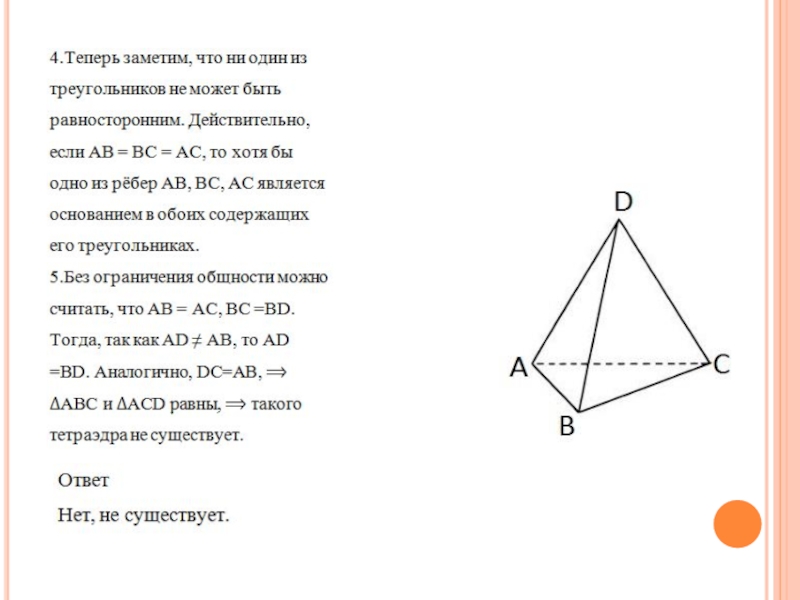
Слайд 24Задача 7
Существует ли тетраэдр, все грани которого равнобедренные треугольники, причём никакие
два из них не равны?
Слайд 27Задача 8
Существует ли многогранник с нечетным числом граней, каждая из которых
многоугольник с нечетным числом сторон.
Решение
Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует.
Решение
Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует.
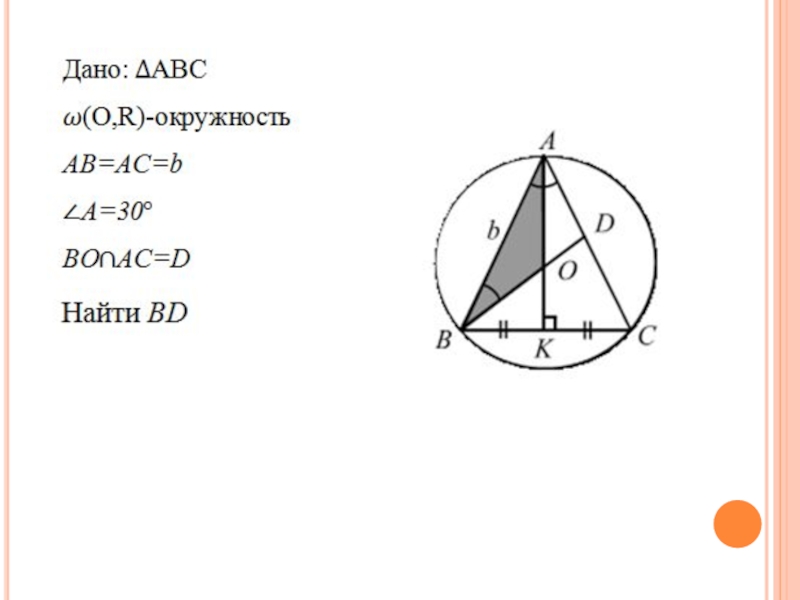
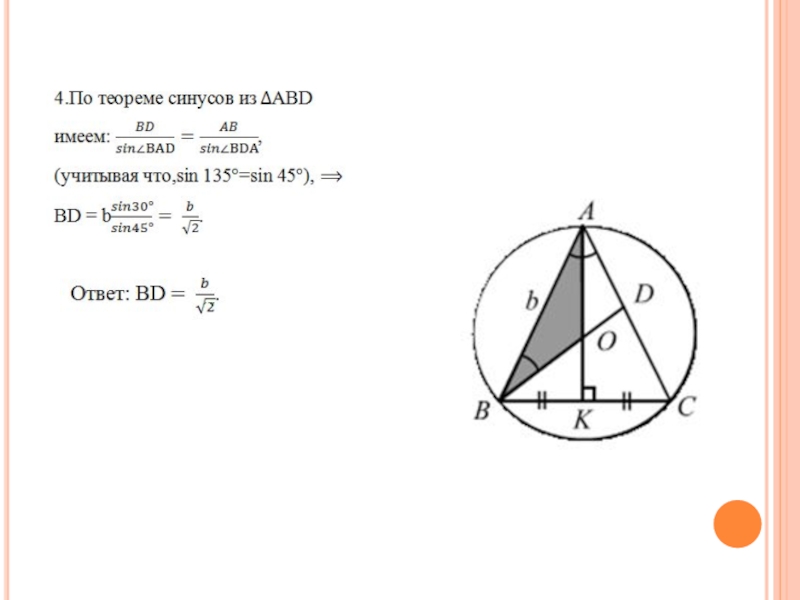
Слайд 28Задача 9
В равнобедренном треугольнике длины боковых сторон и равны b, а
угол при вершине A равен 30°. Прямая, проходящая через вершину B и центр O описанной окружности, пересекает сторону AC в точке D. Найти длину отрезка BD.
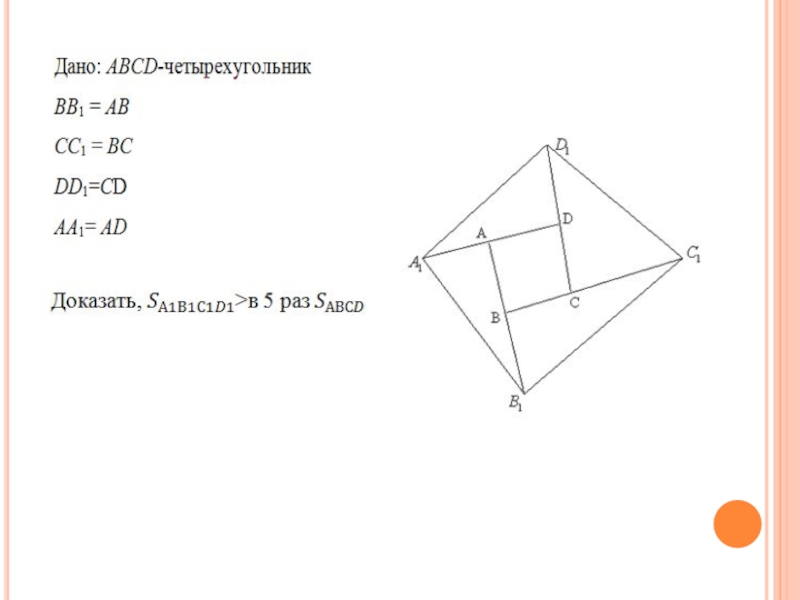
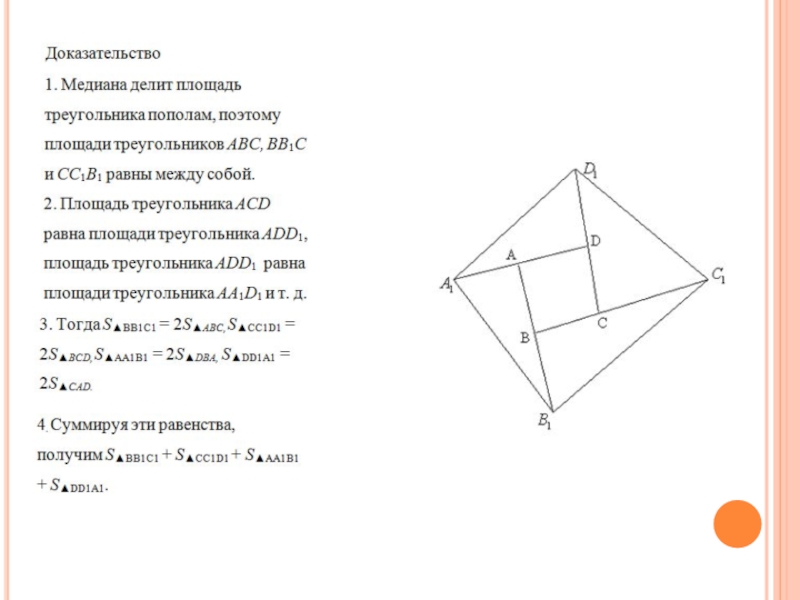
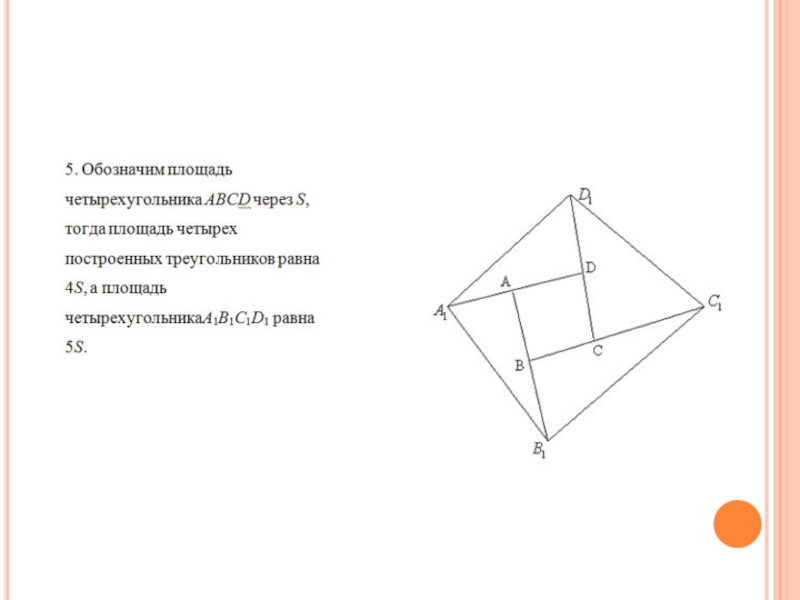
Слайд 32Задача 10
На продолжениях сторон выпуклого четырехугольника АВСD отложены отрезки BB1 =
AB, CC1 = BC, DD1=C и AA1= AD. Докажите, что площадь четырехугольника А1В1С1D1 в 5 раз больше площади четырехугольника АВСD.
Слайд 36Задача 11
Найти площадь треугольника, две стороны которого равны 3 и 7,
а медиана к третьей стороне равна 4.
Слайд 39Задача 12
Найти площадь трапеции, если её основания равны 16 и 44,
а боковые стороны равны 17 и 25.
Слайд 42Задача 13
Основания равнобокой трапеции равны 4 и 6, боковая сторона равна
5. Найти радиус окружности, описанной около этой трапеции.
Слайд 45Задача 14
Около окружности описана равнобокая трапеция с острым углом 60. Найти
отношение длин оснований.
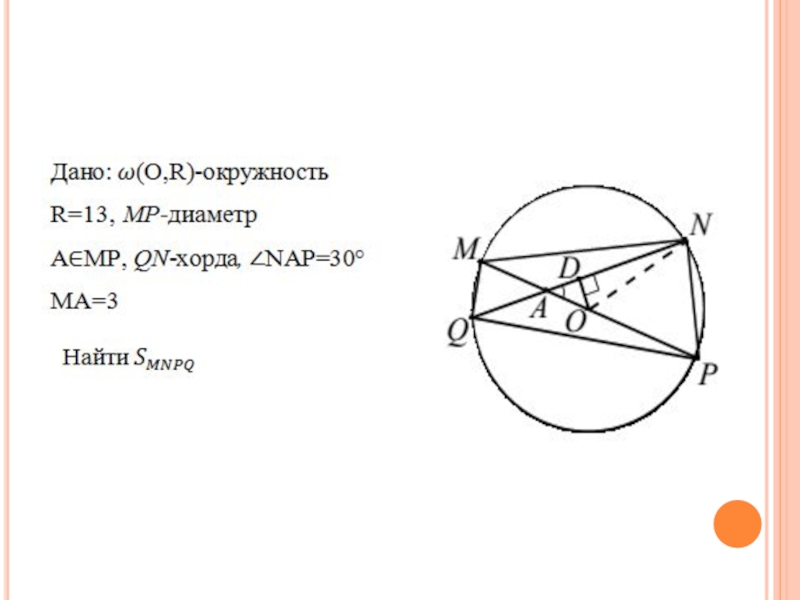
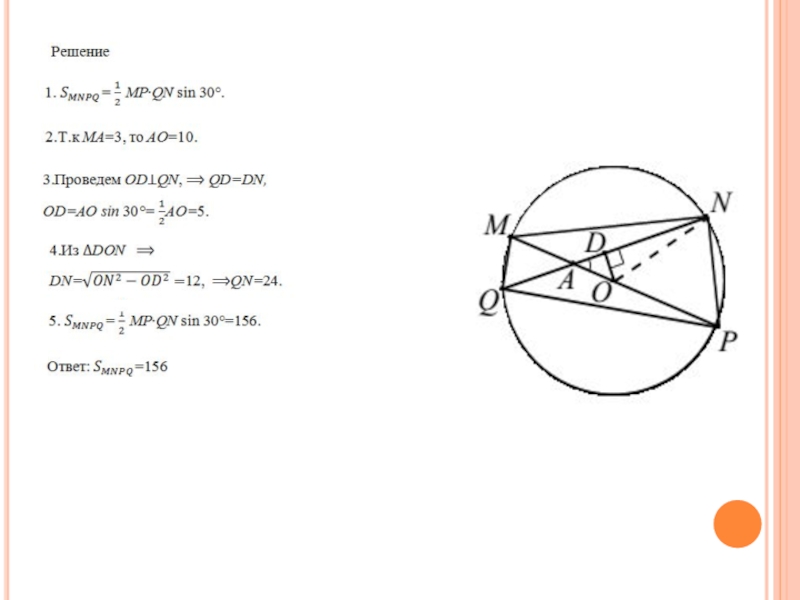
Слайд 48Задача 15
В окружности радиуса 13 через точку А, лежащую на диаметре
MP , под углом 30° проведена хорда QN . Найти площадь четырёхугольника MNPQ, если MA 3.
Слайд 54Задача 17
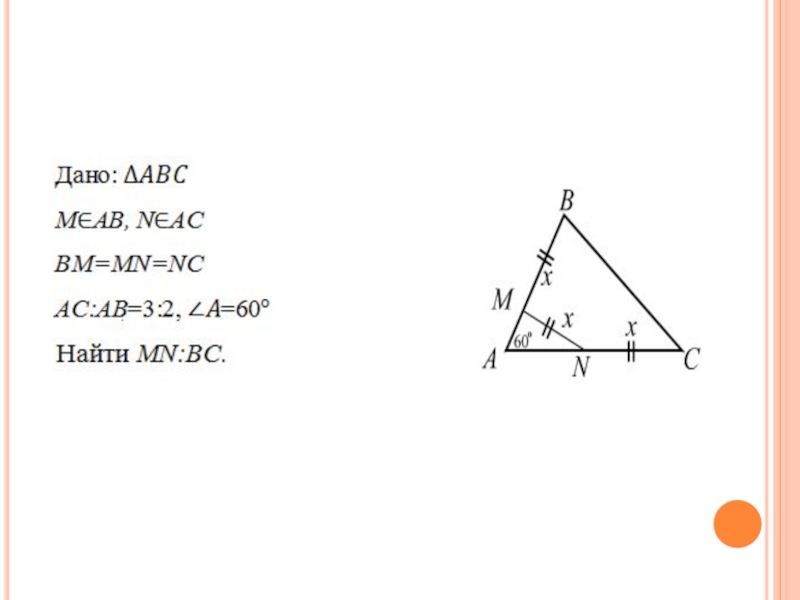
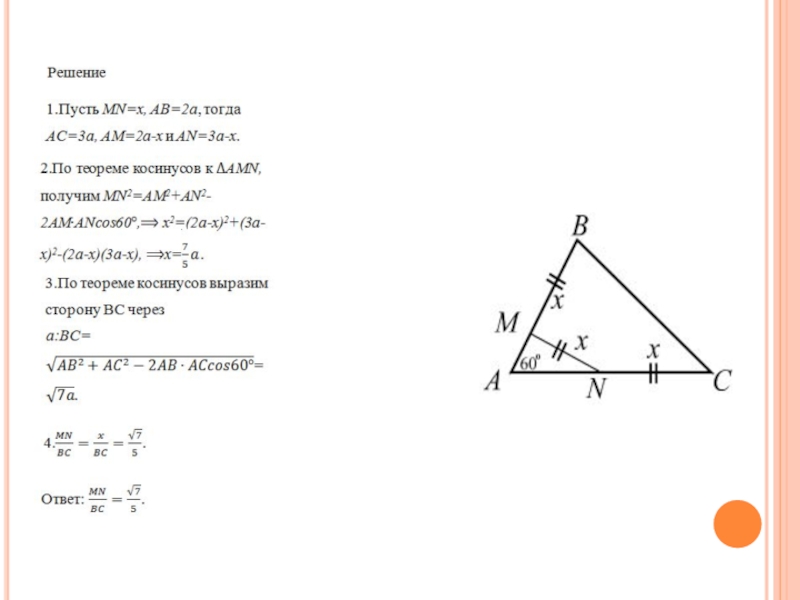
В треугольнике ABC точки M и N лежат на сторонах
AB и AC, при этом BM=MN=NC. Найти отношение MN:BC, если AC:AB=3:2, и угол A равен 60
Слайд 57Задача 18
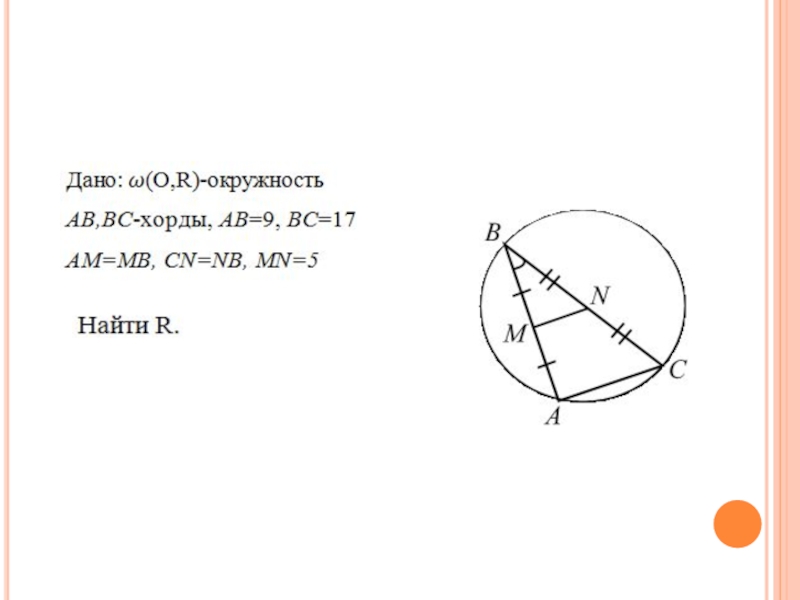
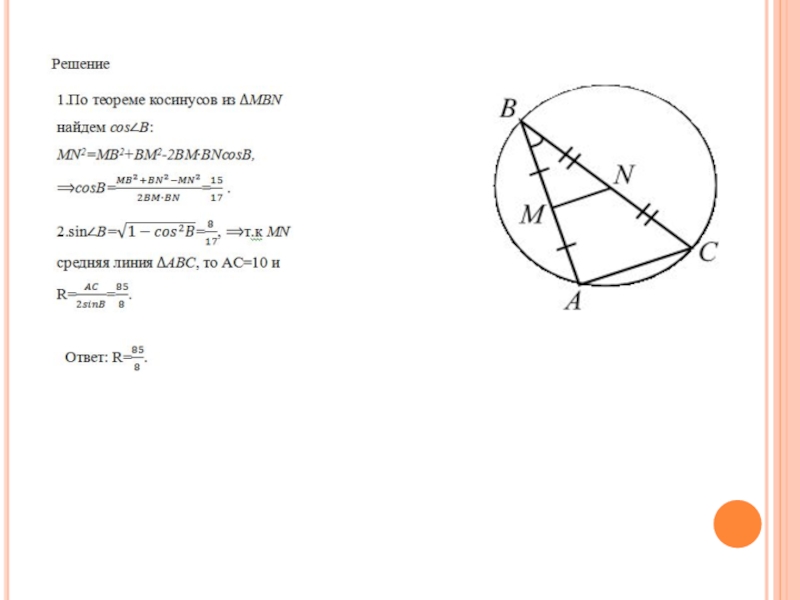
Из одной точки окружности проведены две хорды AB и BC
длиной 9 и 17. Отрезок MN, соединяющий середины этих хорд, равен 5. Найти радиус окружности.
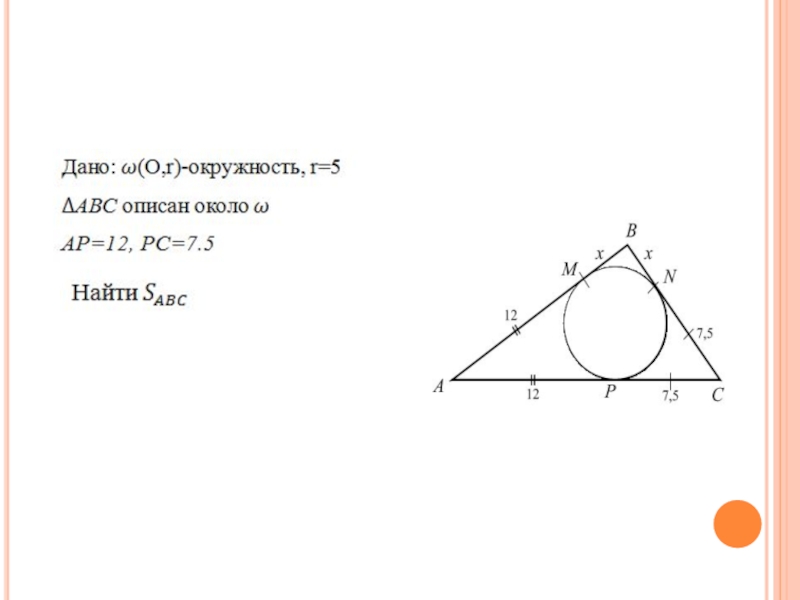
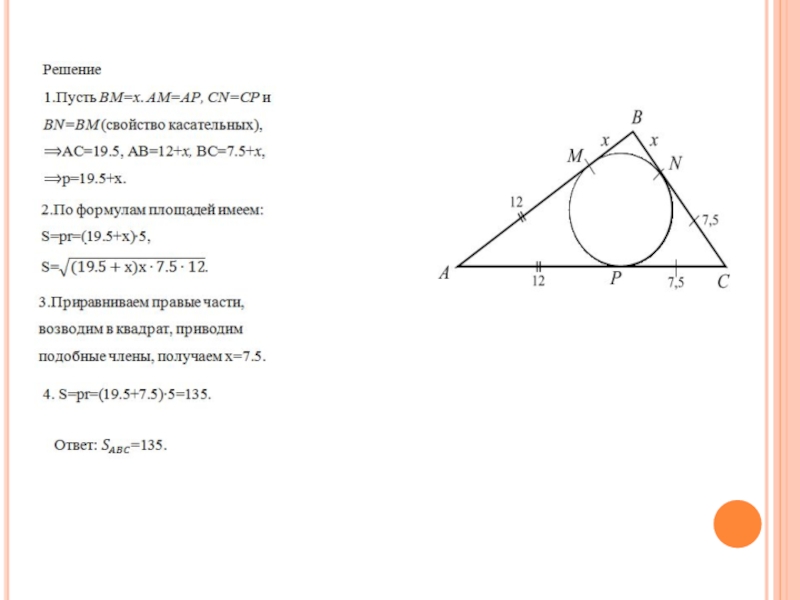
Слайд 63Задача 20
Около окружности радиуса 5 описан треугольник. Найти его площадь, если
одна из его сторон точкой касания делится на отрезки 12 и 7,5.