- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Математика и литература: точки соприкосновения
Содержание
- 1. Презентация по математике на тему Математика и литература: точки соприкосновения
- 2. Часто можно услышать такую фразу: «Ой,
- 3. Проблема: на уроках математики и литературы мало отводится
- 4. В этом романе картинно описан один
- 5. Не доходя футов 500 до гранитной
- 6. – Тебе знакомы начатки геометрии? –
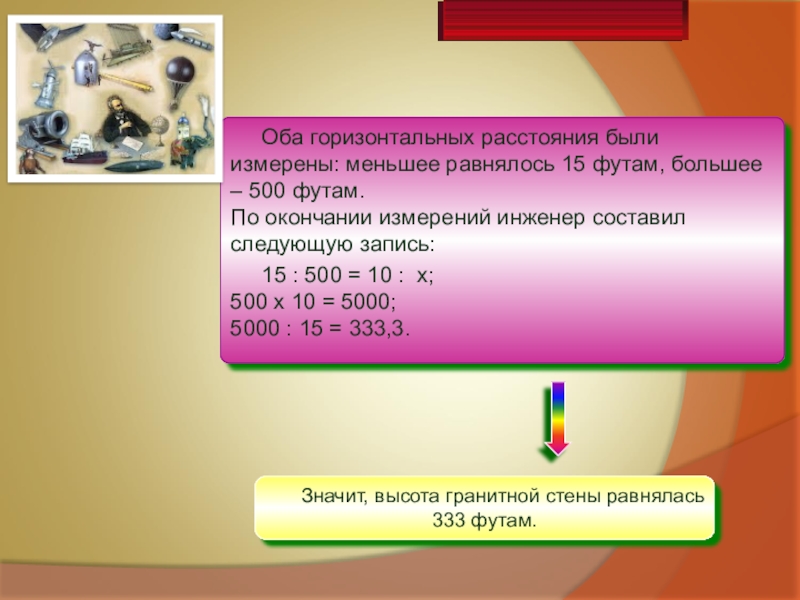
- 7. Оба горизонтальных расстояния были измерены: меньшее равнялось
- 8. Этот метод заключается в том, что нужно
- 9. Ещё один из героев Жюля Верна
- 10. ГЕРОИ ЖЮЛЯ ВЕРНА ИЗМЕРЯЛИ ВЫСОТУ СКАЛЫ .Расстояние
- 11. Любопытно, что в окончательный ответ не входит
- 12. Математика и литература схожи в том, что
- 13. Литературу мы привыкли относить к гуманитарным наукам,
- 14. Слайд 14
- 15. Список использованных источниковБольшая энциклопедия «Кирилл и Мефодий
Слайд 1
Математика и литература – точки соприкосновения
(в произведениях Жюля Верна)
Подготовила
МБОУ Лесногородская СОШ
Иванова Дарья.
Руководитель: Пицель Татьяна Фёдоровна (учитель математики)
Слайд 2 Часто можно услышать такую фразу: «Ой, да что эта математика!
Да, так говорят многие. Но они забывают о том, что именно математика подарила нам такие слова как: гармония,
симметрия,
пропорция.
Слайд 3Проблема: на уроках математики и литературы мало отводится внимания тесному сплетению двух
Актуальность выбранной темы продиктована желанием разрушить стереотип несовместимости этих наук и доказать наличие между ними тесного взаимодействия.
Цель исследования: изучение связи математики и литературы на примере поэтического творчества, и роли математики в жизни поэтов.
Задачи исследования:
Найти факты, подтверждающие единство математики и литературы.
Рассмотреть роль математики для великих поэтов.
Доказать присутствие математики в литературе.
Слайд 4 В этом романе картинно описан один из способов измерения высоких предметов.
–
– Вам понадобится для этого инструмент? – спросил Герберт.
– Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.
Взяв прямой шест, футов 12 длиной, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нёс за ним отвес: просто камень, привязанный к концу верёвки.
Слайд 5
Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер
Слайд 6
– Тебе знакомы начатки геометрии? – спросил он Герберта, поднимаясь
Да.
Помнишь свойства подобных треугольников? – Их сходные стороны пропорциональны. – …Если мы измерим два расстояния: расстояние от колышка до основания шеста и расстояние от колышка до основания стены, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены.
Слайд 7Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее –
15 : 500 = 10 : х; 500 х 10 = 5000; 5000 : 15 = 333,3.
Значит, высота гранитной стены равнялась 333 футам.
Слайд 8Этот метод заключается в том, что нужно вбить в землю шест,
Измерить расстояние от шеста до предмета, измерить высоту шеста и расстояние от макушки человека до основания шеста.
Слайд 9 Ещё один из героев Жюля Верна подсчитывал, какая часть его
Вообразите, что вы обошли земной шар по экватору. Насколько при этом верхушка вашей головы прошла более длинный путь, чем кончик вашей ноги?
Решение:
Ноги прошли путь 2πR, где R – радиус земного шара. Верхушка же головы прошла при этом 2π(R + 1,7), где 1,7 м – рост человека. Разность путей равна м больше, чем ноги.
Итак, голова прошла путь на 10,7 м больше, чем ноги.
Слайд 10ГЕРОИ ЖЮЛЯ ВЕРНА ИЗМЕРЯЛИ ВЫСОТУ СКАЛЫ .
Расстояние от колышка до шеста
Слайд 11
Любопытно, что в окончательный ответ не входит величина радиуса земного шара.
Поэтому результат получится одинаковый и на Земле,
и на Юпитере,
и на самой маленькой планете.
Слайд 12Математика и литература схожи в том, что через них мы познаем
Многих поэтов и писателей издавна притягивала к себе математика. Именно поэтам принадлежат многие образные и вместе с тем исключительно точные высказывания о математике и о числах.
Слайд 13Литературу мы привыкли относить к гуманитарным наукам, а математика требует точности
Литературу, с её интересом к духовному миру человека, и математику, предпочитающую строгий научный подход…
Слайд 15Список использованных источников
Большая энциклопедия «Кирилл и Мефодий »/www.KM.ru/ 1996-2004.
БакиеваА., Саитова
Глейзер Г.И. «История математики в школе, IV – VI классах», изд. Просвещение, М., 1981.
Депман И.Я., Виленкин Н.Я. «За страницами учебника математики», изд. Просвещение, М., 1996.
Научно-теоретический методический журнал «Математика в школе», №3-2001.
Перельман Я.И. «Занимательная геометрия», изд. Технико-теоретической литературы, М., 1950.
Жюль Верн, «Собрание сочинений».
Сайты Интернета.