преподаватель Новиков А. В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Основы программирования и баз данных на тему Языки программирования высокого уровня
Содержание
- 1. Презентация по дисциплине Основы программирования и баз данных на тему Языки программирования высокого уровня
- 2. Метод кубической интерполяцииВ методах полиномиальной аппроксимации при
- 3. Наконец, если f1'f2' < 0, то для
- 4. с коэффициентамиНесложно проверить, что Н3(a) = f1,
- 5. Производная Н'3(х) является квадратичной функцией, непрерывной на
- 6. Его решение, принадлежащее интервалу (a, b), представим
- 7. Следовательно,иЕсли
- 8. После каждого приближения правильность вычислений подтверждается уменьшением
- 9. Для реализации алгоритма кубической аппроксимации можно воспользоваться
- 10. Анализ построенного графика показывает, что исследуемая функция действительно имеет локальный минимум на интервале [a,b]
- 11. Модуль cub имеет список формальных параметров (a,b,),
- 12. При вводе фактических параметровa = 9, b
- 13. Самостоятельная работаЗадача 1. Найти минимум функции
- 14. Литература1. А.В. Аттетков, С.В. Галкин, В.С. Зарубин.
Слайд 1Основы программирования и БД
Тема: Языки программирования высокого уровня
Программная реализация метода кубической
Слайд 2Метод кубической интерполяции
В методах полиномиальной аппроксимации при построении многочлена, аппроксимирующего минимизируемую
Пусть для непрерывно дифференцируемой функции f(x), строго выпуклой на отрезке [a,b], известны значения f1 = f(a), f2 = f(b), f1' = f '(a) и f2' = f '(b). Для строго выпуклой функции производная f'(x) возрастает на отрезке. Поэтому если значения f1' и f2' одного знака, т.е. f1'f2' > 0, то дифференцируемая функция f(x) не имеет стационарных точек на отрезке [a, b] и, следовательно, не имеет на нем точки минимума. Если f1'f2' = 0, то один из концов отрезка является стационарной точкой функции f(x), в которой эта функция имеет минимум.
Слайд 3Наконец, если f1'f2' < 0, то для строго выпуклой функции
f1
Рассмотрим метод поиска точки х* (a, b) при условии
f1'f2' < 0 называемый методом кубической аппроксимации, поскольку в этом случае на отрезке [a, b] можно построить единственный многочлен третьей степени, располагая значениями f1, f2, f1', f2' на концах этого отрезка. Этот многочлен, называемый кубическим интерполяционным многочленом Эрмита, можно преобразовать к виду
Слайд 4с коэффициентами
Несложно проверить, что Н3(a) = f1, H3(b) = f2,
Н'3(a)
Слайд 5Производная Н'3(х) является квадратичной функцией, непрерывной на отрезке [a,b] и имеющей
Из необходимого условия Н'3(х) = 0 экстремума этого многочлена получаем с учетом квадратное уравнение
Слайд 6Его решение, принадлежащее интервалу (a, b), представим в виде
и покажем, что . Действительно, поскольку f1' < 0 и f2' > 0, имеем
Слайд 7Следовательно,
и
Если , то
Слайд 8После каждого приближения правильность вычислений подтверждается уменьшением минимального значения многочлена по
Слайд 9Для реализации алгоритма кубической аппроксимации можно воспользоваться программой MathCAD
Рассмотрим следующую задачу.
Задача.
на интервале [8 12] с точностью ≤ 0,0001.
Решение. Задаем функцию, построим ее график и убедимся, что она имеет минимум на заданном интервале.
Слайд 10Анализ построенного графика показывает, что исследуемая функция действительно имеет локальный минимум
Слайд 11Модуль cub имеет список формальных параметров (a,b,), где а – левая
Слайд 12При вводе фактических параметров
a = 9, b = 11 и
число итераций n = 2;
значение аргумента x = 10.0662
значение функции в точке локального минимума F(10.0662) =
-4.1217;
модуль произведения значений производных 1 – ого порядка.
Последние три строки программы – это проверка полученного результата с помощью встроенной функции вычисления минимума функции одной переменной minimize. Функция имеет два входных аргумента: имя исследуемой функции и начальную точку x из интервала [a, b]. В последней строке кода отображено значение функции в точке локального минимума.
Отсюда видно, что результаты расчетов совпадают.
Слайд 13Самостоятельная работа
Задача 1. Найти минимум функции
Задача 2. Найти минимум функции F(x) = x4 + х2 + x + 1 на интервале [-1 0] с точностью до 0,0001.
(Ответ: х = - 0.3855)
Задача 3. Найти минимум функции на интервале [0 10] с точностью до 0,0001. (Ответ: х = 3)
Задача 4. Найти минимум функции F(x) = x3 + 16х2 - 10x – 21 на интервале [0 6] с точностью до 0,0001. (Ответ: х = 0.3038)
Слайд 14Литература
1. А.В. Аттетков, С.В. Галкин, В.С. Зарубин. Методы оптимизации: Учеб. для
2. Половко А.М., Ганичев И.В. MathCAD для студента. – СПб.: БХВ – Петербург, 2006. – 336 с.



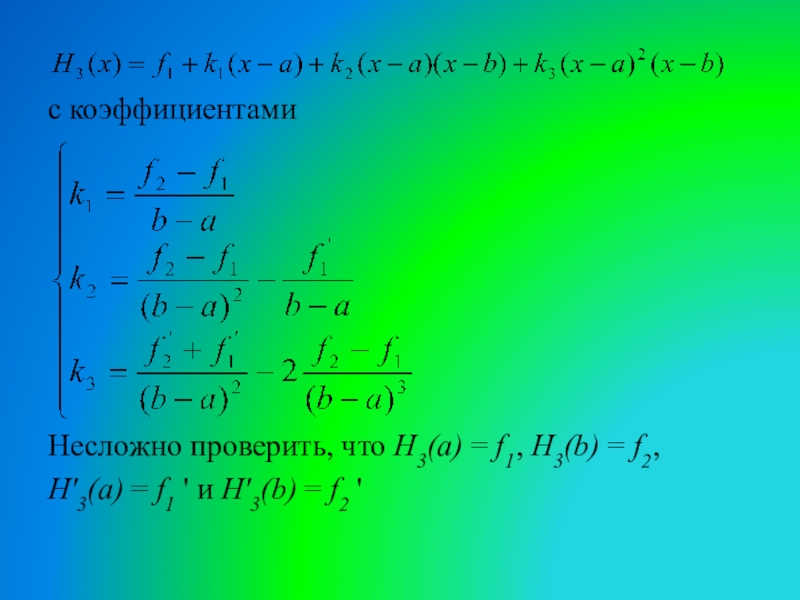
![Презентация по дисциплине Основы программирования и баз данных на тему Языки программирования высокого уровня Производная Н'3(х) является квадратичной функцией, непрерывной на отрезке [a,b] и имеющей Производная Н'3(х) является квадратичной функцией, непрерывной на отрезке [a,b] и имеющей на его концах различные знаки. Поэтому](/img/thumbs/cd5c0c1fa4fa7e766b019958bf1c932b-800x.jpg)
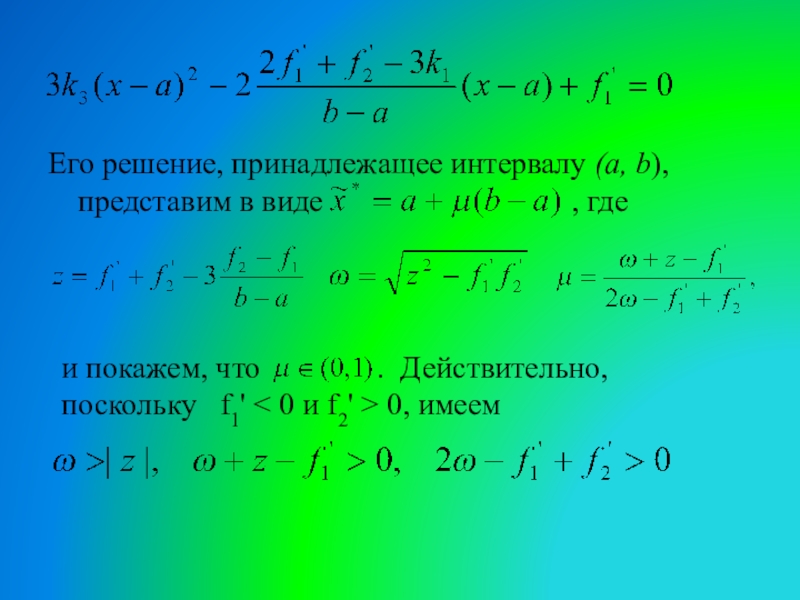



![Презентация по дисциплине Основы программирования и баз данных на тему Языки программирования высокого уровня Анализ построенного графика показывает, что исследуемая функция действительно имеет локальный минимум на интервале [a,b] Анализ построенного графика показывает, что исследуемая функция действительно имеет локальный минимум на интервале [a,b]](/img/thumbs/5c3a6c849c3f802d1b2b763b09f4ab77-800x.jpg)









