преподаватель Новиков А. В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Информационные технологии в профессиональной деятельности на тему Решение транспортной задачи в EXCEL
Содержание
- 1. Презентация по дисциплине Информационные технологии в профессиональной деятельности на тему Решение транспортной задачи в EXCEL
- 2. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ Транспортная задача – одна из
- 3. В общем виде задачу можно представить следу-ющим
- 4. Если
- 5. Рассмотрим задачу Определение эффективного варианта доставки товаров к
- 6. Обозначим через xij количество груза, перевозимого из
- 7. Теперь перенесем математическую мо-дель задачи в таблич-ную
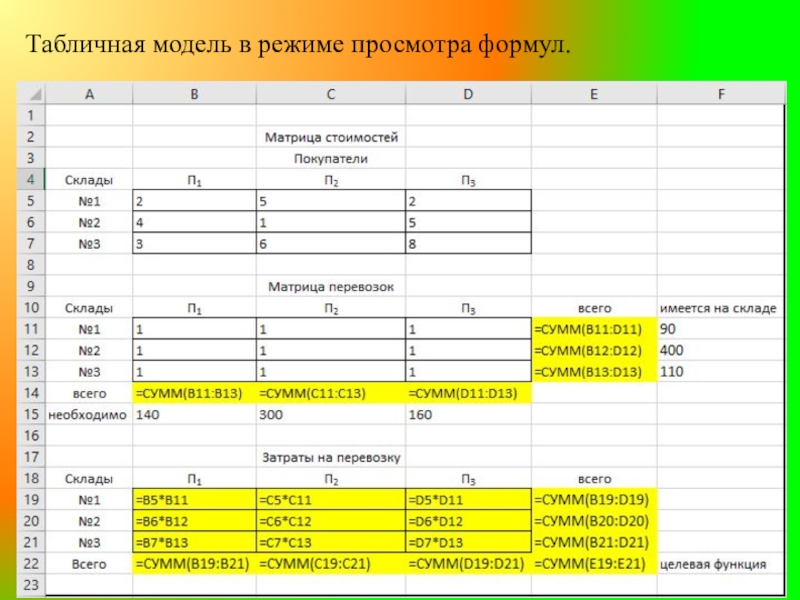
- 8. Табличная модель в режиме просмотра формул.
- 9. Исходная настройка табличной модели произведена, можно приступать
- 10. В диалоговом окне ПАРАМЕТРЫ ПОИСК РЕШЕНИЯ не
- 11. В соответствии с полученным решением:со склада №
- 12. ЛитератураКосоруков О.А., Мищенко А.В.: Учебник – М.
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ Транспортная задача – одна из распростра-ненных задач линейного программирования. Ее цель – разработка наиболее рациональ-ных путей и способов транспортирования това-ров, устранение чрезмерно дальних, встречных и повторных перевозок. Все это сокращает время продвижения товаров, уменьшает
Слайд 1Информационные технологии в профессиональной деятельности
Тема: Решение ТранспортнОЙ задачИ
С ПОМОЩЬЮ EXCEL
Разработал
Слайд 2ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
Транспортная задача – одна из распростра-ненных задач линейного программирования.
Ее цель – разработка наиболее рациональ-ных путей и способов транспортирования това-ров, устранение чрезмерно дальних, встречных и повторных перевозок.
Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.
Слайд 3 В общем виде задачу можно представить следу-ющим образом: в m пунктах
производства А1, А2, … Аm имеется однородный груз в количестве соответственно а1, а2, … аm. Этот груз необходимо доставить в n пунктов назначения B1, B2,…, Bn в количестве соответ-ственно b1, b2,…, bn.
Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна cij.
Требуется составить план перевозок, позволяю-щий вывезти все грузы и имеющий минимальную стоимость.
В зависимости от соотношения между суммар-ными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
Стоимость перевозки единицы груза (тариф) из пункта Ai в пункт Bj равна cij.
Требуется составить план перевозок, позволяю-щий вывезти все грузы и имеющий минимальную стоимость.
В зависимости от соотношения между суммар-ными запасами груза и суммарными потребностями в нем транспортные задачи могут быть закрытыми и открытыми.
Слайд 4Если
, то задача называется закрытой.
Если , то открытой.
Обозначим через xij количество груза, перевозимого из пункта Ai в пункт Bj. Рассмотрим закрытую транспортную задачу.
Математическая модель закрытой транспортной задачи имеет вид
при ограничениях
Оптимальным решением задачи является матрица Хопт = (xij)mn, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.
Если , то открытой.
Обозначим через xij количество груза, перевозимого из пункта Ai в пункт Bj. Рассмотрим закрытую транспортную задачу.
Математическая модель закрытой транспортной задачи имеет вид
при ограничениях
Оптимальным решением задачи является матрица Хопт = (xij)mn, удовлетворяющая системе ограничений и доставляющая минимум целевой функции.
xij 0, i = 1,…,m j = 1,…,n
Слайд 5Рассмотрим задачу
Определение эффективного варианта доставки товаров к потребителю
На складах А1, А2,
А3 имеются запасы продукции в количествах 90, 400 и 110 т соответственно.
Потребители В1, В2, В3 должны получить эту продукцию в количествах 140, 300 и 160 т соответственно.
Найти такой вариант доставки грузов, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (у.е.)
Потребители В1, В2, В3 должны получить эту продукцию в количествах 140, 300 и 160 т соответственно.
Найти такой вариант доставки грузов, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (у.е.)
Слайд 6 Обозначим через xij количество груза, перевозимого из пункта Ai в пункт
Bj.
Математическую модель задачи представим в развернутом виде.
при ограничениях:
Математическую модель задачи представим в развернутом виде.
при ограничениях:
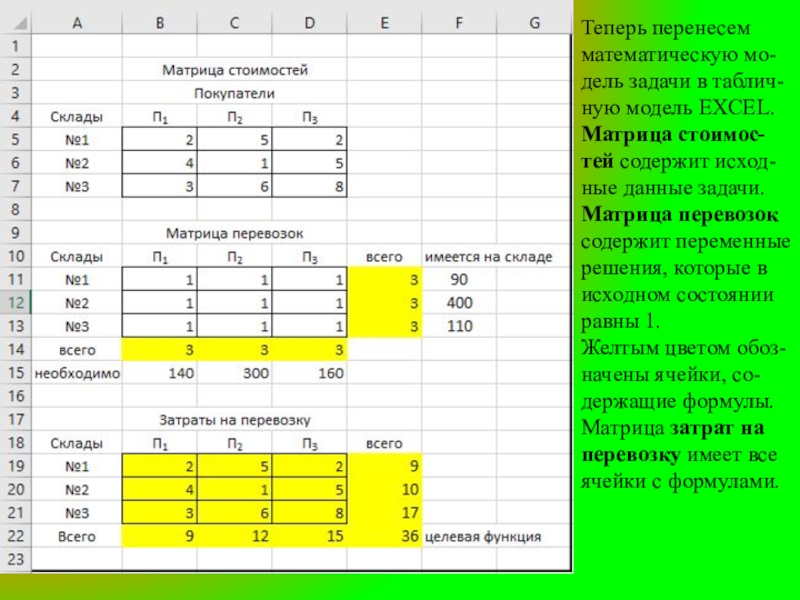
Слайд 7Теперь перенесем математическую мо-дель задачи в таблич-ную модель EXCEL.
Матрица стоимос-тей
содержит исход-ные данные задачи.
Матрица перевозок содержит переменные решения, которые в исходном состоянии равны 1.
Желтым цветом обоз-начены ячейки, со-держащие формулы.
Матрица затрат на перевозку имеет все ячейки с формулами.
Матрица перевозок содержит переменные решения, которые в исходном состоянии равны 1.
Желтым цветом обоз-начены ячейки, со-держащие формулы.
Матрица затрат на перевозку имеет все ячейки с формулами.
Слайд 9 Исходная настройка табличной модели произведена, можно приступать к поиску оптимального решения.
Запускаем
средство ПОИСК РЕШЕНИЯ. В одноименном диалоговом окне задаем адрес целевой ячейки F22, устанавливаем переключатель в положение – минимальному значению, указываем диапазон изменяемых ячеек В11:D13, списком задаем ограничения. После этих манипуляций диалоговое окно должно выглядеть так, как показано на рис. 2.
Слайд 10 В диалоговом окне ПАРАМЕТРЫ ПОИСК РЕШЕНИЯ не забываем установить флажки ЛИНЕЙНАЯ
МОДЕЛЬ, НЕОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ и АВТОМАТИЧЕСКОЕ МАСШТАБИРОВАНИЕ. Наконец, в диалоговом окне ПОИСК РЕШЕНИЯ щелкаем на кнопке ВЫПОЛНИТЬ и получаем решение на рис. 3.
Слайд 11 В соответствии с полученным решением:
со склада № 1 компании надо перевезти
весь имею-щийся там груз (в объеме 90 т) на склад покупателя ПЗ (ячейка D11), при этом затраты на транспортировку составят 180 у. е. (ячейка D19);
со склада № 2 следует 30, 300 и 70 т. продукции отправить на склады покупателей П1, П2 и П3 соответ-ственно (ячейки С12:D12), затраты на перевозку соста-вят 120, 300 и 350 у. е. (ячейки B20:D20);
со склада № 3 110 т. продукции отправятся на склад покупателя П1 (ячейка В13) при затратах 330 у. е. (ячей-ка В21).
Общая стоимость всех перевозок составит 1280 у. е. (значение целевой функции в ячейке F22).
со склада № 2 следует 30, 300 и 70 т. продукции отправить на склады покупателей П1, П2 и П3 соответ-ственно (ячейки С12:D12), затраты на перевозку соста-вят 120, 300 и 350 у. е. (ячейки B20:D20);
со склада № 3 110 т. продукции отправятся на склад покупателя П1 (ячейка В13) при затратах 330 у. е. (ячей-ка В21).
Общая стоимость всех перевозок составит 1280 у. е. (значение целевой функции в ячейке F22).
Слайд 12Литература
Косоруков О.А., Мищенко А.В.: Учебник – М. Издательство «Экзамен», 2003. –
448 с.
2. Минько А.А. Принятие решений с помощью Excel. – М.: Эксмо, 2007. – 240 с.
2. Минько А.А. Принятие решений с помощью Excel. – М.: Эксмо, 2007. – 240 с.