- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Олимпиадные задачи 8-9 классы
Содержание
- 1. Олимпиадные задачи 8-9 классы
- 2. Произведение двух натуральных чисел, каждое из
- 3. Известно, что Какие значения может
- 4. Найдите все пары натуральных чисел, удовлетворяющих уравнению:
- 5. Из натурального числа вычли сумму его
- 6. Прямоугольник разделен на квадратики со стороной 1см.
- 7. Прямоугольник разделен на квадратики со стороной 1см.
- 8. В 8 «А» классе Вовочка учится
- 9. Пусть в классе n учеников из которых
- 10. На вопрос о возрасте его детей математик
- 11. Третьему ребенку 1 год.Пусть первому и второму
- 12. Решение: Пусть у первого брата x рублей, у
- 13. Когда Винни-Пух пришел в гости к Кролику,
- 14. Решение По условию 3м + 4с +
- 15. Прямоугольный лист бумаги согнули так, как показано
- 16. Прямоугольный лист бумаги согнули так, как показано
Слайд 1Школа одаренных детей «Импульс» ОЛИМПИАДНЫЕ ЗАДАЧИ
8-9 классы
Бусыгина Наталия Сергеевна,учитель математики
Слайд 2 Произведение двух натуральных чисел, каждое из которых не делится нацело на
, каждое из чисел в своем разложении на простые множители может содержать только двойки и пятерки.
Оба множителя не могут присутствовать в разложении одного числа, иначе оно будет делиться на 10.
Следовательно, одно из чисел , а другое
Значит,
Ответ: 133.
Слайд 4Найдите все пары натуральных чисел, удовлетворяющих уравнению: x2 – xy – 2x
Решение:
Исходное уравнение x2 – xy – 2x + 3y = 11 преобразуем к виду y(x – 3) = x2 – 2x – 11, откуда y = (x2 – 2x – 11)/(x – 3) = x + 1 – 8/(x – 3). Следовательно (обратите внимание на дробь), возможны варианты x = 1; 2; 4; 5; 7; 11. Находя соответствующие значения переменной y, получаем пары чисел: (1; 6), (2; 11), (4; -3), (5; 2), (7; 6), (11; 11). С учётом того, что числа должны быть натуральным, удовлетворять уравнению будут следующие 5 пар чисел: Ответ: (1; 6), (2; 11), (5; 2), (7; 6), (11; 11).
Слайд 5 Из натурального числа вычли сумму его цифр и получили 2007. Каким
Исходное число должно быть четырехзначным.
- цифры, то
может быть любой цифрой.
Ответ: любое натуральное число от 2010 до 2019.
Слайд 6Прямоугольник разделен на квадратики со стороной 1см. В каждом квадратике записано
Слайд 7Прямоугольник разделен на квадратики со стороной 1см. В каждом квадратике записано
Пусть в прямоугольнике а строк и b столбцов, тогда его площадь ab=2008.
Сумма всех чисел в прямоугольнике, с одной стороны, равна а, а с другой стороны, равна 2b. Следовательно, a=2b.
1004 – не является квадратом натурального числа.
Ответ: нет, не может.
Слайд 8 В 8 «А» классе Вовочка учится хуже всех. Педсовет решил, что
Слайд 9Пусть в классе n учеников из которых k – двоечники.
Если Вовочка
Поэтому
.
Если Вовочку выгонят, то двоечников станет k-1, а учеников в классе будет n-1.
Разделив почленно первое уравнение на второе, получим
Процент двоечников
Ответ:28%
В 8 «А» классе Вовочка учится хуже всех. Педсовет решил, что либо Вовочка к концу четверти должен исправить двойки, либо его исключат. Если Вовочка исправит двойки, то в классе будет 24% двоечников, а если его выгонят, то двоечников станет 25%. Какой процент двоечников в 8 «А» сейчас?
Слайд 10На вопрос о возрасте его детей математик ответил: «У нас с
Слайд 11Третьему ребенку 1 год.
Пусть первому и второму год назад было соответственно
В это же время, суммарный возраст родителей был равен (45+2х) лет, т.к каждый из них за это время повзрослел на х (или у, это без разницы) лет.
Суммарный возраст семьи в то время, когда родился третий ребенок – 70 лет.
Суммарный возраст детей
Ответ: 8лет, 5 лет, 1 год.
Слайд 12Решение: Пусть у первого брата x рублей, у второго – y рублей, у
Выразим все переменные через z и подставим в первое уравнение системы:
Ответ: 3507 рублей
У четырёх братьев всего 32000 рублей. Если деньги первого брата увеличить на 7 рублей, а деньги второго – уменьшить на 7 рублей, третьего – увеличить в 7 раз, а четвёртого – уменьшить в 7 раз, то у братьев станет денег поровну. Сколько рублей было у второго из братьев первоначально?
Слайд 13Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки
Слайд 14Решение
По условию 3м + 4с + 2в > 2м + 3с +
По условию же 3м + 4с + 2в > 4м + 2с + 3в, откуда 2с > м + в.
Складывая последнее неравенство с неравенством (*), получаем м + 3с > м + 3в,
откуда с > в.
Ответ : от сгущенки.
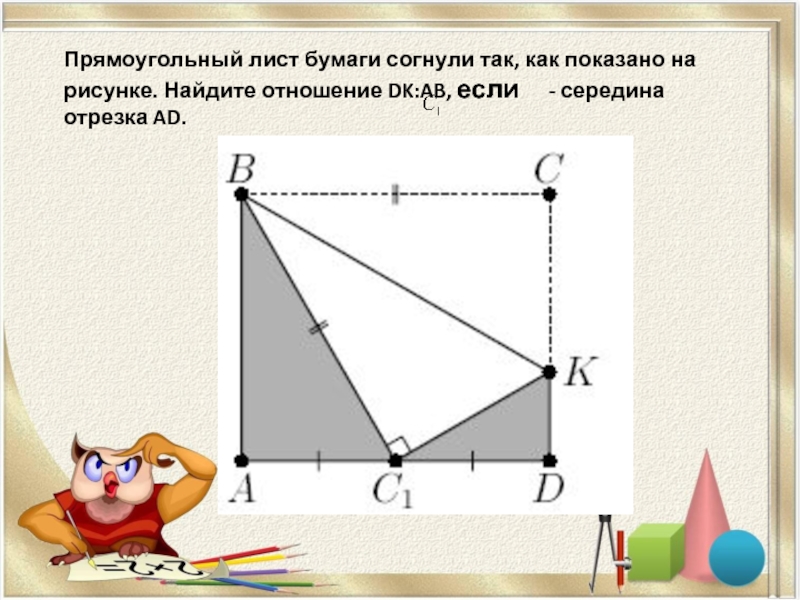
Слайд 15Прямоугольный лист бумаги согнули так, как показано на рисунке. Найдите отношение
Слайд 16Прямоугольный лист бумаги согнули так, как показано на рисунке. Найдите отношение
Т.к. треугольник равен треугольнику , то .
В прямоугольном треугольнике
катет, противолежащий углу ,
равен половине гипотенузы, т.е.
, тогда ,
.
Поэтому
.
Ответ: