- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конические сечения и их применения в технике
Содержание
- 1. Конические сечения и их применения в технике
- 2. Цель: изучение конических сечений и их применение
- 3. Конические сечения - это плоские кривые, которые
- 4. Виды конических сеченийКонические сечения могут быть трёх
- 5. 2) Секущая плоскость параллельна одной из касательных
- 6. 3) Секущая плоскость пересекает обе полости конуса;
- 7. Применение конических сечений в техникеКонические сечения часто
- 8. Построение конических сеченийИзучая конические сечения как пересечения
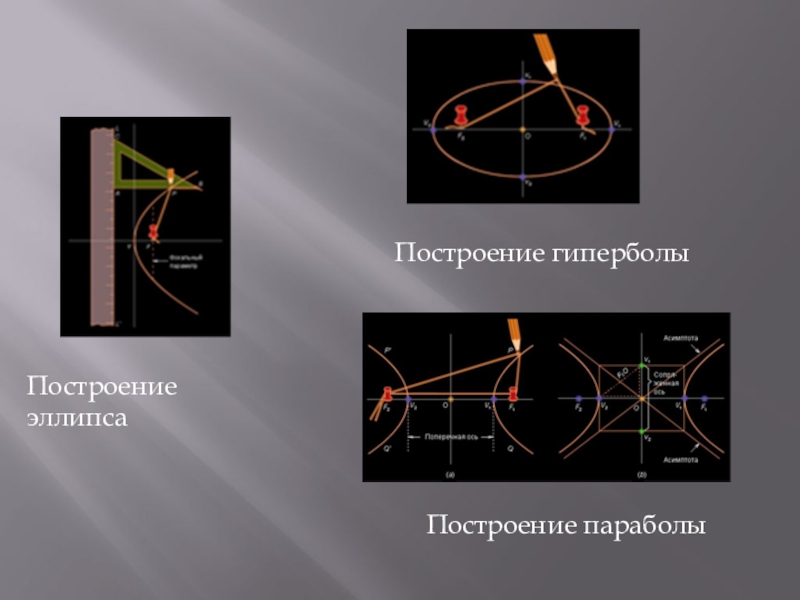
- 9. Построение эллипсаПостроение гиперболыПостроение параболы
- 10. Спасибо за внимание
Цель: изучение конических сечений и их применение в технике.Задачи: изучить виды конических сечений; изучить применение их в технике.
Слайд 2Цель:
изучение конических сечений и их применение в технике.
Задачи:
изучить виды
конических сечений;
изучить применение их в технике.
изучить применение их в технике.
Слайд 3Конические сечения
- это плоские кривые, которые получаются пересечением прямого кругового
конуса плоскостью, не проходящей через его вершину. Конические сечения впервые предложил использовать древнегреческий геометр Менехм, живший в IV веке до нашей эры, при решении задачи об удвоении куба. Коническими сечениями являются эллипсы, гиперболы или параболы.
Слайд 4Виды конических сечений
Конические сечения могут быть трёх типов:
1) Секущая плоскость пересекает
все образующие конуса в точках одной его полости; линия пересечения есть замкнутая овальная кривая — эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса.
Слайд 52) Секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении
получается незамкнутая, уходящая в бесконечность кривая — парабола, целиком лежащая на одной полости.
Слайд 63) Секущая плоскость пересекает обе полости конуса; линия пересечения — гипербола
— состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.
Слайд 7Применение конических сечений в технике
Конические сечения часто встречаются в природе и
технике. Например, орбиты планет, обращающихся вокруг Солнца, имеют форму эллипсов. В большинстве телескопов-рефлекторов, где применяются параболические зеркала, а также в антеннах радаров и специальных микрофонах с параболическими отражателями. В мощных прожекторах и автомобильных фарах используются параболические зеркала. Законе Бойля (связывающего давление и объем идеального газа) и законе Ома, задающего электрический ток как функцию сопротивления при постоянном напряжении.
Слайд 8Построение конических сечений
Изучая конические сечения как пересечения плоскостей и конусов, древнегреческие
математики рассматривали их и как траектории точек на плоскости. Было установлено, что эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна; параболу – как геометрическое место точек, равноудаленных от заданной точки и заданной прямой; гиперболу – как геометрическое место точек, разность расстояний от которых до двух заданных точек постоянна.
Эти определения конических сечений как плоских кривых подсказывают и способ их построения с помощью натянутой нити.
Эти определения конических сечений как плоских кривых подсказывают и способ их построения с помощью натянутой нити.