«В геометрии существует два сокровища: первое – теорема Пифагора, второе – золотое сечение. Первое можно сравнить с мерой золота, второе – с драгоценным камнем».
Кеплер
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Золотое сечение, 1 часть
Содержание
- 1. Золотое сечение, 1 часть
- 2. Давайте выясним, что общего между древнеегипетскими пирамидами,
- 3. Золотое сечение – (золотая пропорция, деление в
- 4. Эту пропорцию принято обозначать греческой буквой φ и она равна: b:а = с:bЧему равно волшебное число?
- 5. Построение ряда отрезков золотой пропорции
- 6. Последовательность натуральных чиселUk=1,1,2,3,5,8,13,21,34,55,89,144,233,377,...,каждый член которой начиная с
- 7. Практическое знакомство с золотым сечением начинают с
- 8. Принято считать, что понятие о золотом делении
- 9. Платон привел формулировку золотой пропорции: «Для соединения
- 10. Пифагорейцы были первыми, кто обратил в символ
- 11. В последовательностях звездчатых пятиугольников (а) и десятиугольников
- 12. В природе очень
- 13. Паук плетет паутину спиралеобразно. Спиралью
- 14. Золотые пропорции в строении молекулы ДНК
- 15. Выяснилось, что в расположениилистьев на ветке (филотаксис),
- 16. "Порхающими цветами" называют бабочек-этих удивительных созданий природы.
- 17. Неудивительно, что стрекоза выглядит столь совершенной, ведь
- 18. Золотое сечение присутствует
- 19. Закономерности «золотой» симметрии проявляются в энергетических
- 20. каждое звено в системе сердца, начиная с
- 21. Золотое сечение в человеческом телеВ 1855 г. немецкий
- 22. Сумма двух первых фаланг пальца в соотношении
- 23. Трудно оторвать глаза от
- 24. По наблюдениям Л.Сабанеева, в музыкальных
- 25. Многими исследователями было замечено, что стихотворения подобны
- 26. 792 стихотворения русского гения Александра Пушкина были
- 27. Не дорого ценю я громкие права, От
- 28. Известно, что Сергей Эйзенштейн искусственно построил
Слайд 1Золотое сечение
Автор презентации: Мартусевич Татьяна Олеговна - преподаватель ГБПОУ «Педагогический колледж
Слайд 2Давайте выясним, что общего между древнеегипетскими пирамидами, картиной Леонардо да Винчи
Слайд 3Золотое сечение –
(золотая пропорция, деление в крайнем и среднем
гармоническое деление, число Фидия, φ)
— деление отрезка на части в таком соотношении,
при котором большая часть относится к меньшей,
как сумма (весь отрезок) к большей.
Что такое "золотое сечение"?
Слайд 4Эту пропорцию принято обозначать
греческой буквой φ и она равна:
b:а
Чему равно волшебное число?
Слайд 6Последовательность натуральных чисел
Uk=1,1,2,3,5,8,13,21,34,55,89,144,233,377,...,
каждый член которой начиная с третьего равен сумме двух
Отношение последующего члена ряда к предыдущему стремится к коэффициенту золотого сечения
Числа Фибоначчи
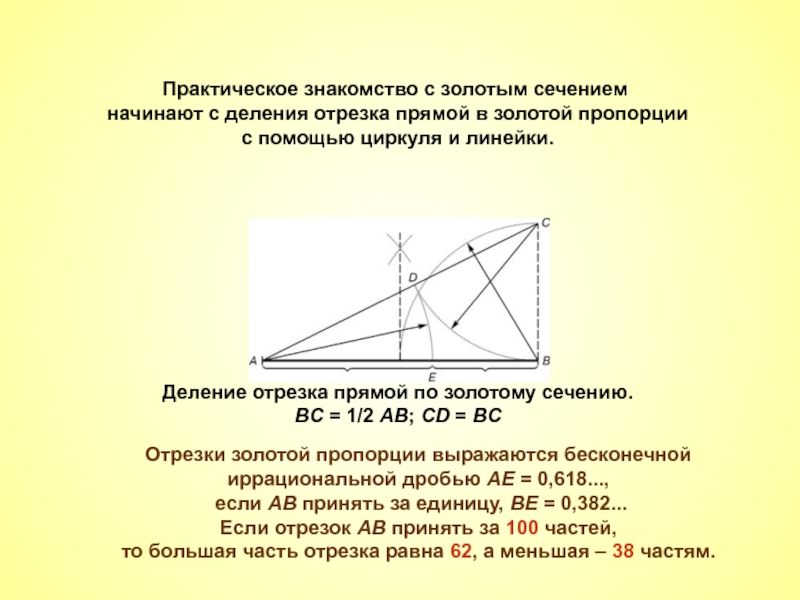
Слайд 7Практическое знакомство с золотым сечением
начинают с деления отрезка прямой в
с помощью циркуля и линейки.
Деление отрезка прямой по золотому сечению.
BC = 1/2 AB; CD = BC
Отрезки золотой пропорции выражаются бесконечной
иррациональной дробью AE = 0,618...,
если АВ принять за единицу, ВЕ = 0,382...
Если отрезок АВ принять за 100 частей,
то большая часть отрезка равна 62, а меньшая – 38 частям.
Можем построить
Слайд 8Принято считать, что понятие о золотом делении ввел в научный обиход
Из истории
Пифагор
Слайд 9Платон привел формулировку золотой пропорции: «Для соединения двух частей с третьей
Платон
Евклид
Во 2-й книге «Начал» Евклида дается
геометрическое построение
золотого деления.
Слайд 10
Пифагорейцы были первыми,
кто обратил в символ пятиконечную звезду.
Редкое обилие
в одной геометрической фигуре
приводило пифагорейцев в священный восторг!
Лучи пентаграммы делят друг друга в золотой пропорции:
целое так относится к большей части, как большая часть к меньшей.
Пентаграмма
Столь необычайно пропорциональное строение пентаграммы,
красота её внутреннего математического содержания являются
основой и красоты её внешней формы.
Пентаграммы пропорциональна и, значит, красива.
Не случайно и сегодня пятиконечная звезда реет на флагах
едва ли не половины стран мира!
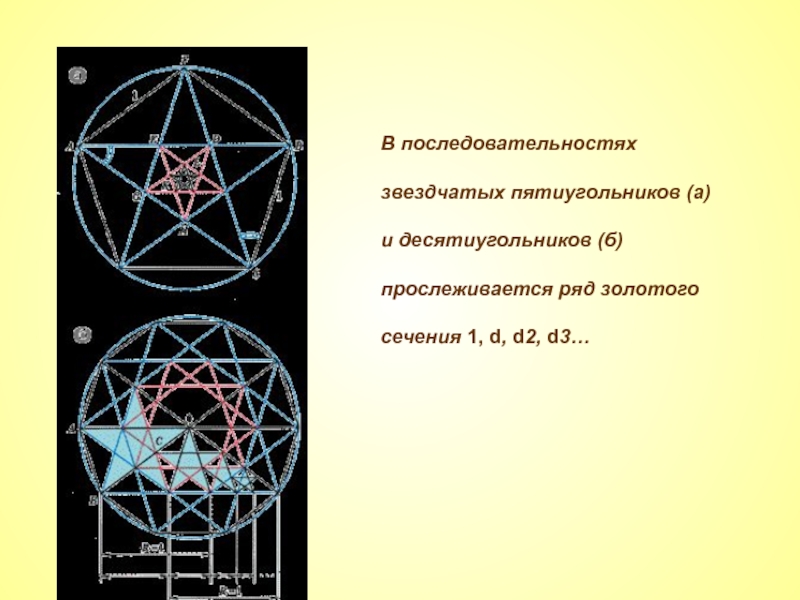
Слайд 11В последовательностях звездчатых пятиугольников (а) и десятиугольников (б) прослеживается ряд золотого
Слайд 12 В природе очень распространены спирали.
Представление о
если не сказать о спирали.
Спираль построенную по принципу золотого сечения описал Архимед.
Архимед и золотая спираль
Спираль Архимеда
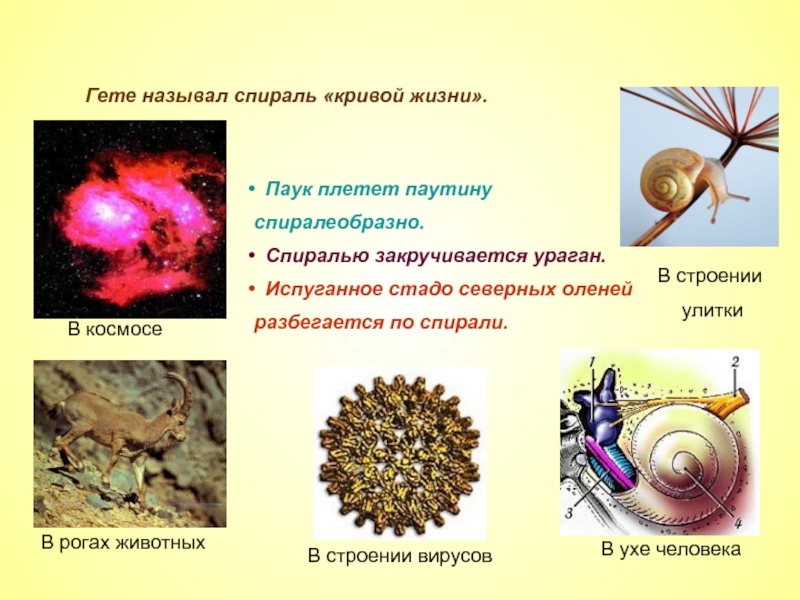
Слайд 13 Паук плетет паутину спиралеобразно.
Спиралью закручивается ураган.
Испуганное
Гете называл спираль «кривой жизни».
В космосе
В рогах животных
В строении вирусов
В ухе человека
В строении
улитки
Кривая жизни-золотая спираль
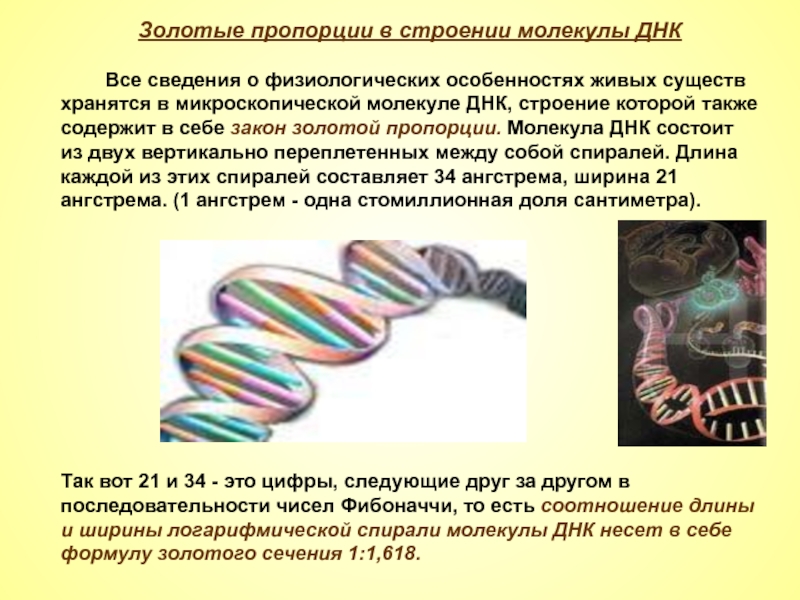
Слайд 14Золотые пропорции в строении молекулы ДНК
Все
Так вот 21 и 34 - это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.
Слайд 15Выяснилось, что в расположении
листьев на ветке (филотаксис),
семян подсолнечника, шишек сосны
проявляет себя ряд Фибоначчи,
а стало быть, проявляет себя
закон золотого сечения.
Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.
Совместная работа ботаников и математиков
пролила свет на эти удивительные
явления природы.
Слайд 16"Порхающими цветами" называют бабочек-этих удивительных созданий природы. Их крохотное тело несут
Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8.
Бабочка
Слайд 17Неудивительно, что стрекоза выглядит столь совершенной, ведь она создана по законам
Стрекоза
Слайд 18
Золотое сечение присутствует в строении всех кристаллов,
Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.
Золотое сечение в строении снежинок
Слайд 19Закономерности «золотой» симметрии проявляются
в энергетических переходах элементарных частиц
в планетарных и космических системах
в генных структурах живых организмов
в строении отдельных органов человека и тела в целом
в биоритмах
в функционировании головного мозга, сердца и зрительного восприятия
Слайд 20каждое звено в системе сердца, начиная с субклеточных параметров кардиомиоцита до
Золотое сечение в нашем сердце
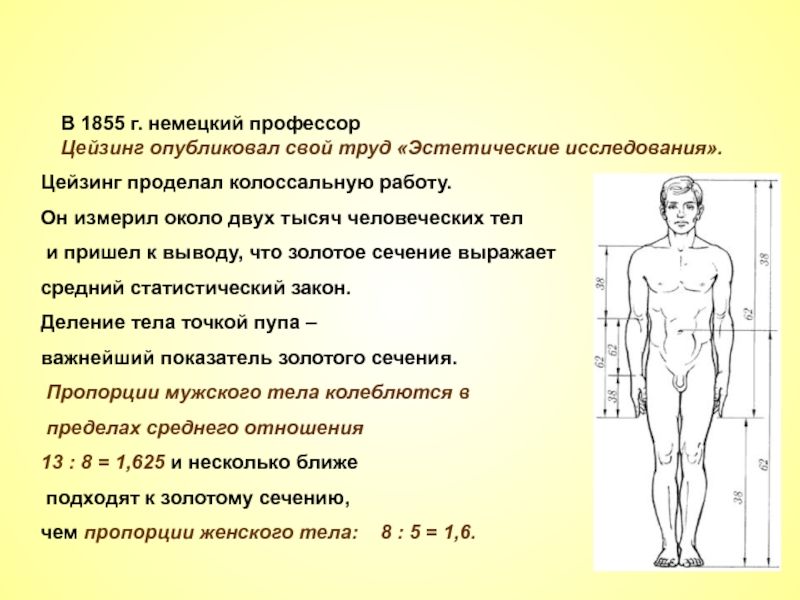
Слайд 21Золотое сечение в человеческом теле
В 1855 г. немецкий профессор
Цейзинг опубликовал свой труд
Цейзинг проделал колоссальную работу.
Он измерил около двух тысяч человеческих тел
и пришел к выводу, что золотое сечение выражает
средний статистический закон.
Деление тела точкой пупа –
важнейший показатель золотого сечения.
Пропорции мужского тела колеблются в
пределах среднего отношения
13 : 8 = 1,625 и несколько ближе
подходят к золотому сечению,
чем пропорции женского тела: 8 : 5 = 1,6.
Слайд 22Сумма двух первых фаланг пальца в соотношении со всей длиной пальца
У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.
Рука человека
Слайд 23 Трудно оторвать глаза от красоты, она так притягательна,
Коэф_зол_сеч1 = 1.618; Коэф_зол_сеч2 = 0.618; Коэф_зол_сеч3 = 0.382;
Золотое сечение в одежде
Слайд 24
По наблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется
В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. Количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338.
Наибольшее количество музыкальных произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Во всем царит гармонии закон,
И в мире все суть ритм, аккорд и тон
Джон Драйден
Математика музыки
Слайд 25Многими исследователями было замечено, что стихотворения подобны музыкальным произведениям; в них
Представляет несомненный интерес анализ романа "Евгений Онегин", сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55!
Гармония поэзии
Слайд 26792 стихотворения русского гения Александра Пушкина были изучены на предмет существования
Основные результаты исследования таковы. Главными функциями золотого сечения в творчестве Пушкина являются:
* структурообразующая функция (325 или 84% стихотворений из 385 стихотворений с золотым сечением),
* выделение главной мысли (304 или 79%),
*прорисовка кульминации (270 или 70%).
Слайд 27Не дорого ценю я громкие права, От коих не одна кружится голова. Я
Одно из последних стихотворений Пушкина "Не дорого ценю я громкие права..." состоит из 21 строки и в нем выделяется две смысловые части: в 13 и 8 строк. Характерно, что и первая часть этого стиха (13 строк) по смысловому содержанию делится на 8 и 5 строк, то есть все стихотворение построено по законам золотой пропорции.
Слайд 28 Известно, что Сергей Эйзенштейн искусственно построил
Фильм Броненосец Потёмкин по
Он разбил ленту на пять частей.
В первых трёх действие разворачивается на корабле.
В двух последних — в Одессе, где разворачивается восстание.
Этот переход в город происходит точно в точке золотого сечения.
Да и в каждой части есть свой перелом, происходящий
по закону золотого сечения.
В кадре, сцене, эпизоде происходит некий скачок в развитии темы:
сюжета, настроения.
Эйзенштейн считал, что так как такой переход близок
к точке золотого сечения, он воспринимается как наиболее
закономерный и естественный.