- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи на подобие треугольников в ЕГЭ
Содержание
- 1. Задачи на подобие треугольников в ЕГЭ
- 2. Цель урока:повторить признаки подобия треугольников;детально рассмотреть задачу С4 ЕГЭ;ввести понятие ортотреугольника
- 3. Определение подобных треугольников Два треугольника
- 4. Признаки подобия треугольниковI признак подобия треугольников
- 5. Признаки подобия треугольниковII признак подобия треугольников
- 6. Признаки подобия треугольниковIII признак подобия треугольников
- 7. Слайд 7
- 8. Задача С4Точки А1, В1, С1 – основания
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Определение ортотреугольника
- 14. Свойства ортотреугольника
- 15. Слайд 15
- 16. Слайд 16
Цель урока:повторить признаки подобия треугольников;детально рассмотреть задачу С4 ЕГЭ;ввести понятие ортотреугольника
Слайд 2Цель урока:
повторить признаки подобия треугольников;
детально рассмотреть задачу С4 ЕГЭ;
ввести понятие ортотреугольника
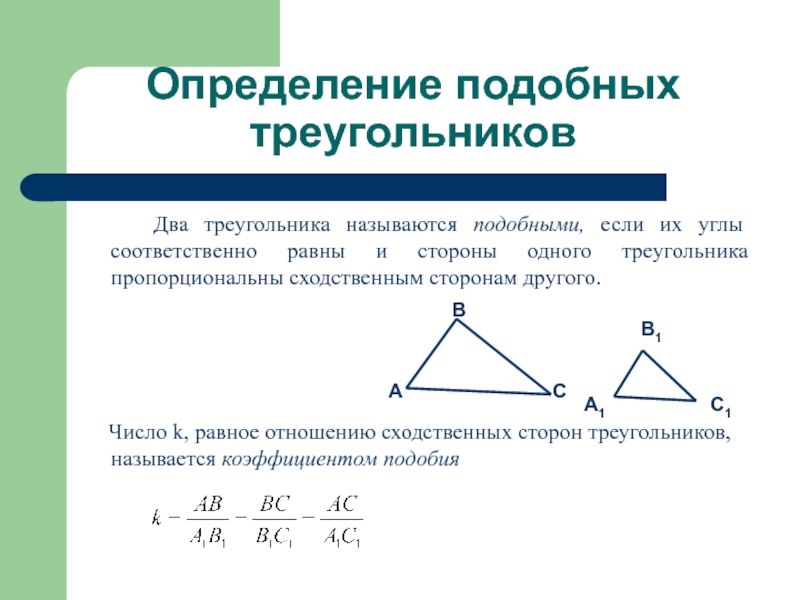
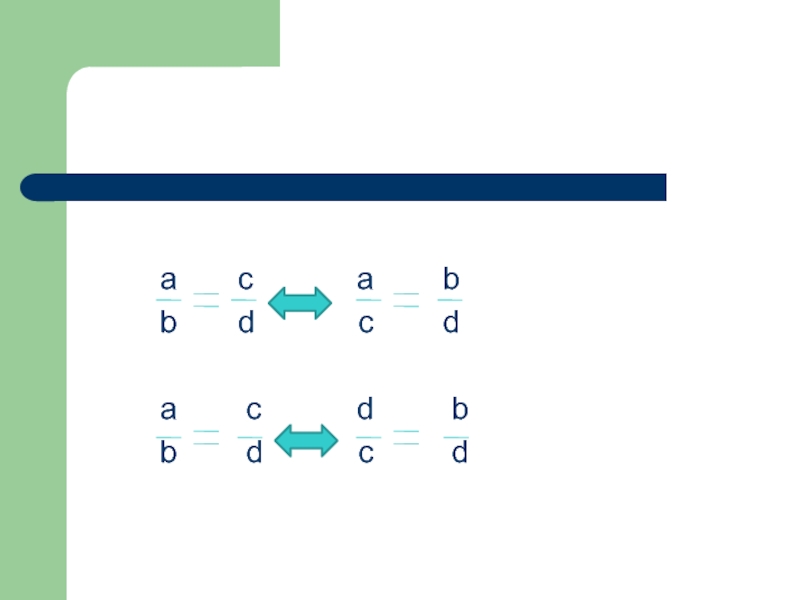
Слайд 3Определение подобных треугольников
Два треугольника называются подобными, если их
углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
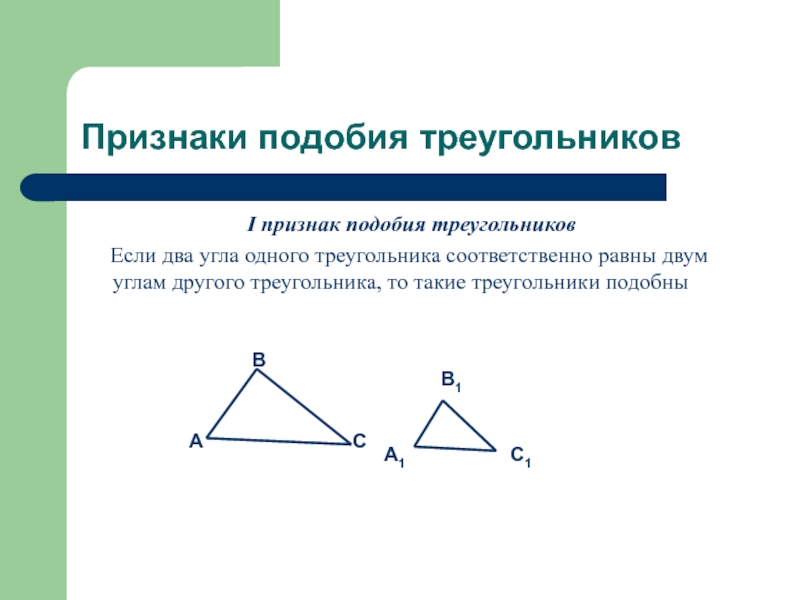
Слайд 4Признаки подобия треугольников
I признак подобия треугольников
Если два угла
одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны
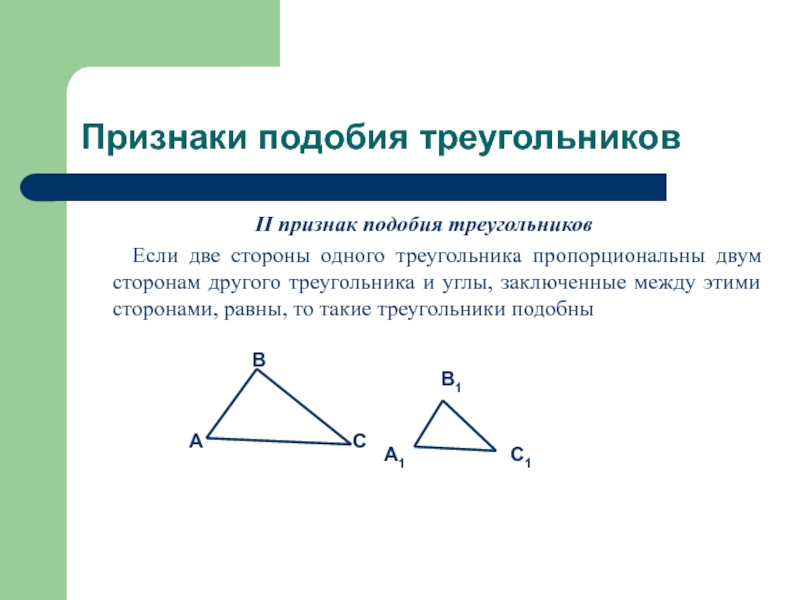
Слайд 5Признаки подобия треугольников
II признак подобия треугольников
Если две стороны
одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
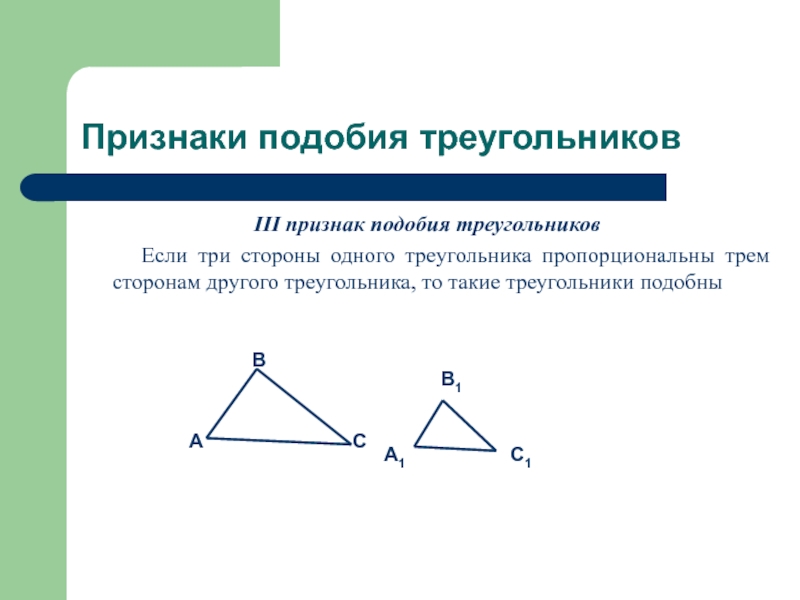
Слайд 6Признаки подобия треугольников
III признак подобия треугольников
Если три стороны
одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
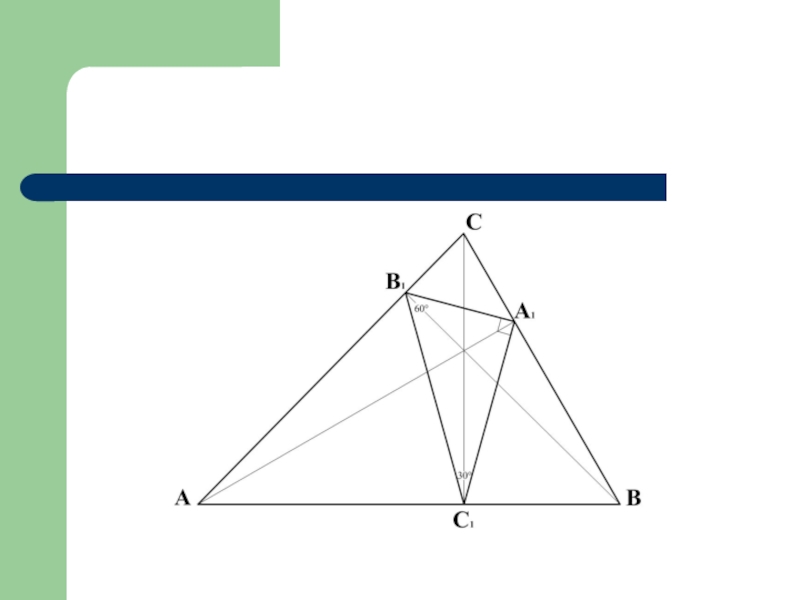
Слайд 8Задача С4
Точки А1, В1, С1 – основания высот треугольника АВС. Углы
треугольника А1В1С1 равны 90º, 60º и 30º. Найдите углы треугольника АВС.
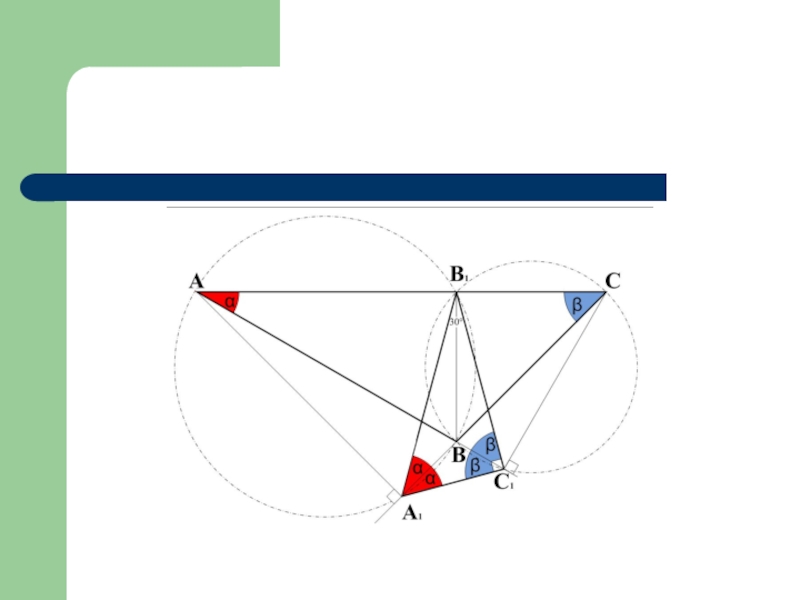
Слайд 14Свойства ортотреугольника
Ортотреугольник отсекает треугольники, подобные данному.
Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.
3. Высоты треугольника являются биссектрисами ортотреугольника.
4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .
5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.
