- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи к ак средство реализации метапредметных связей.
Содержание
- 1. Задачи к ак средство реализации метапредметных связей.
- 2. «Источник и цель математики – в
- 3. Математическое моделирование, алгоритмизация и программирование. 1.)... Первобытная
- 4. Если записать эту историю на математическом языке,
- 5. 5).Трава на лугу растет одинаково густо и
- 6. 6) Записать алгоритм нахождения наибольшего общего делителя
- 7. 7).Известно, что 1кг лимонов содержит 150мг витамина
- 8. Практическая работа № 1Возьмите лист бумаги и
- 9. Практическая работа № 2Одни ребята берут лист
- 10. 9класс. Практическая работа по теме «Характеристика разброса.
- 11. Практическая работа “Определение плотности твердого тела. Нахождение
- 12. Исследовательский проект ( Статистические исследования) « Влияние
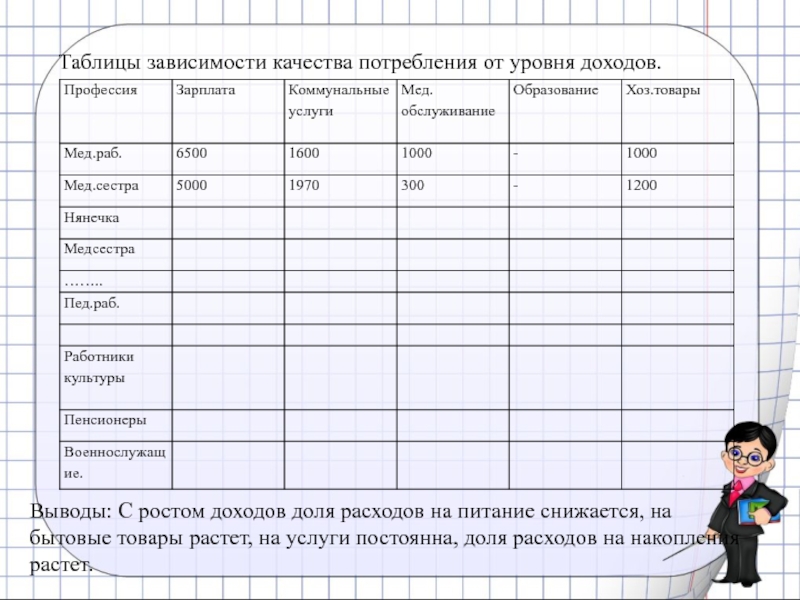
- 13. Таблицы зависимости качества потребления от уровня доходов.
- 14. 11класс. Урок по теме: Производная. Наибольшее и
- 15. Математика-Физика9). Материальная точка вращается вокруг оси по
- 16. 5 Класс Тема: Разнообразный мир линий.
- 17. Натуральные числа. Математика+История Индийский правитель, желая отблагодарить
- 18. Математика -ФизикаКогда мы включаем, выключатель и сразу
- 19. 6 класс: Проценты.Математика+Химия . Сплав двух
- 20. Математика-Литература№7« Читал я где-тоЧто царь однажды воинам
- 21. Прикладные задачи.Каким может быть наибольший объем бандероли
- 22. нетрадиционные формы уроковМатематический аукцион, Своя Игра, Урок -Путешествие .
- 23. Математический аукцион.Тема : Формулы и буквы.Обобщающий урок.6классУчитель Артемьева И.Н.
- 24. ЛОТ №1 Самый крупный из представленных сегодня.
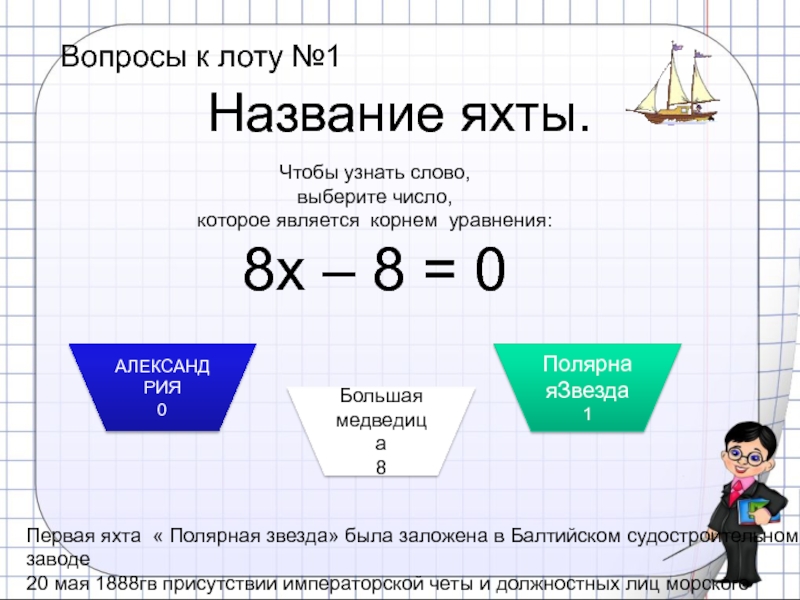
- 25. Вопросы к лоту №1Название яхты.Чтобы узнать
- 26. Когда была спущена на воду первая яхта?Какая
- 27. Лот №4
- 28. Решите уравнения :
- 29. Лот № 7Знаете ли вы , что
- 30. Решите уравнение и подставьте его корень вместо
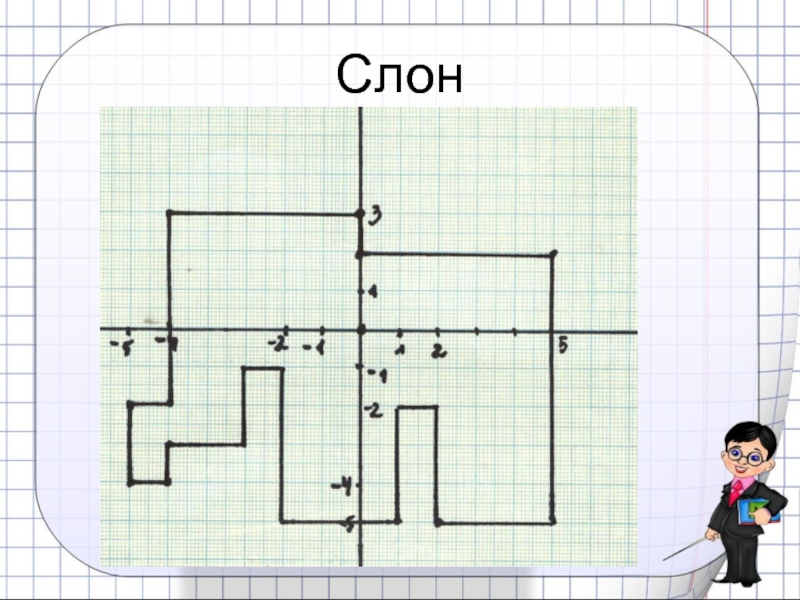
- 31. Слон
- 32. Спасибо за внимание.
Слайд 1Задачи как средство реализации метапредметных связей.
Артемьева И.Н.
Учитель математики МБОУ сош №18
Слайд 3Математическое моделирование, алгоритмизация и программирование.
1.)... Первобытная мама сорвала с дерева
Слайд 4Если записать эту историю на математическом языке, то получится вот что.
ЗАДАНИЯ.
1. Нарисуйте модель ситуации, когда первобытная мама делила яблоки между детьми.
2. . Заполни таблицу недостающими данными, взяв их из текста.
3.Составь уравнение.
2) Решите в уме, например, такую древнеегипетскую задачу. Количество и его четвертая часть дают вместе 15. Найти количество.
3). Решите задачу с помощью уравнения.
Спросил некто некоего учителя: «Сколько имеешь учеников у себя, так как хочу отдать сына к тебе в учение». Учитель ответил: «Если ко мне придет учеников еще столько же, сколько имею, и пол столько, и четвертая часть, и твой сын, тогда будет у меня учеников 100». Сколько было у учителя учеников?
Слайд 55).Трава на лугу растет одинаково густо и быстро. Известно, что 70
Заданные в задаче величины — количество коров и числом дней — не связаны непосредственно, поэтому введем следующие вспомогательные неизвестные — параметры для установления связи между основными величинами. Пусть на лугу первоначально было "а" единиц травы, и ежедневно на нем, вырастает "b" единиц травы. Пусть каждая корова за 1 день съедает "c" единиц травы.
За 24 дня всего вырастет (а+24b) единиц травы, которую за это время съедают 70 коров. Они съедают 24*70с=1680с, следовательно
a+24b=1680с. (1)
По условию, что 30 коров съедают всю траву за 60 дней, получаем:
а+60b=1800с. (2)
За 96 дней на лугу вырастет всего, а+96b единиц травы, которую съедят искомое х. число коров, они съедят всего 96х*с единиц травы, следовательно, получим такое уравнение:a+96b=96х*с. Решаем систему и получаем . Ответ: 20 коров.
Слайд 66) Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел
6) Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида).
Алгоритм может быть следующим:
задать два числа;
если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
определить большее из чисел;
заменить большее из чисел разностью большего и меньшего из чисел;
повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.
Слайд 77).Известно, что 1кг лимонов содержит 150мг витамина С, а 1кг яблок
Решение системы уравнений:
у = 0,25 у = 0,25 у = 0,25
у = -2х +1 -2х +1 = 0,25 х = 0,375
Далее находим:
F (х, у) = 60· 0,375 + 40·25 = 16,25р.
Итак, чтобы дневной рацион содержал 75мг витамина С и чтобы затраты при этом были минимальные, человеку необходимо ежедневно съедать 0,375кг апельсинов и 0,25кг яблок.
Слайд 8Практическая работа № 1
Возьмите лист бумаги и перегните его пополам. Теперь
Слайд 9Практическая работа № 2
Одни ребята берут лист бумаги. Согнув его пополам,
Другие берут салфетку, сложенную вчетверо, и вырезают снежинку.
А теперь внимательно рассмотрим полученные фигуры. Линии сгиба вырезанной фигуры делит ее на две равные части. Такая фигура называется симметричной относительно прямой (линии сгиба), а линия сгиба - осью симметрии.
Рассмотрим снежинку. Сколько у нее получилось линий сгиба(осей симметрии)?
Можно сделать вывод. Если внимательно рассмотреть геометрические фигуры, то среди них есть фигуры, имеющие одну или несколько осей симметрии. А есть фигуры, у которых осей симметрии нет.
Слайд 109класс. Практическая работа по теме «Характеристика разброса. Статистическое и оценивание и
Каждый ученик получил распечатку небольшого фрагмента текста и изображение клавиатуры.
Были распределены буквы. Каждый ученик внимательно подсчитывал количество встреч со своей буквой. Результат подсчета записывался на рисунке клавиатуры на соответствующую кнопку. Вывод чаще всего буквы встречались в центре клавиатуры.(60-70)
Слайд 11Практическая работа “Определение плотности твердого тела. Нахождение абсолютной и относительной погрешностей
Учащимся сообщается порядок выполнения работы. На столах у них – оборудование для практической работы. (Работу выполняют в парах)
Порядок выполнения работы.
Найти массу бруска (использовать шкалу динамометра, проградуированную в граммах).
Найти объем бруска, для чего измерить длину, ширину, высоту. Расчетная формула:
V = abc.
Вычислить плотность бруска. Расчетная формула: r = m/V.
Учитывая, что брусок алюминиевый, сравнить полученное значение плотности с табличным.
Вычислить абсолютную и относительную погрешности экспериментального результата.
В ходе вычислений использовать компьютер.
Результаты измерений и вычислений записать в таблицу.
Название вещества: алюминий. Таблица 2.
Слайд 12Исследовательский проект ( Статистические исследования) « Влияние доходов на уровень жизни населения»-10
Цели: Исследования реальной обстановки методом выборочных наблюдений и получить достоверную информацию о доходах и расходах населения в своем поселке.
Задачи:
Организовать сбор первичных статистических данных
Получить данные как по отдельным жителям поселка , так и в совокупности.
Добиться максимально достоверных результатов.
Слайд 13Таблицы зависимости качества потребления от уровня доходов.
Выводы: С ростом доходов доля
Слайд 1411класс. Урок по теме: Производная. Наибольшее и наименьшее значения функции.
Математика-Химия, Математика-Биология.
Задача
Пусть функция Q=f(t) описывает концентрацию некоторого лекарства в крови в момент времени. Какую величину будет описывать производная этой функции f (t),в момент временит? Решение: Пусть концентрация в крови некоторого лекарства. А описывается функциейf(t)=3-1\2t. Найдите скорость изменения концентрации. А в момент времени t.Полученное значение, концентрация лекарства. А в крови у бывает с постоянной скоростью.
Задача №2Пусть p=p(t) описывает размер популяции бактерий в момент в момент времени t , тогда v=p(t) – скорость роста популяции в момент времени t. Определите скорость роста популяции в момент времени tه=5ч,10ч., если популяция в момент времени t насчитывает p(t)=3000+100t2.
Задача№3. В питательную среду вносят популяцию из 1000 бактерий. Численность популяции растет по закону p(t)=1000+1000t/100+t2,t больше или равно) и выражается в часах. Найдите наибольший рост популяции за сутки.
Слайд 15Математика-Физика
9). Материальная точка вращается вокруг оси по закону =(t), где t
10) Цепь висячего моста располагается по дуге параболы у=рх2.
Пролет моста имеет длину 50м, а стрела провеса f=5м. Определить величину угла провеса в крайней точке моста. [4]
Слайд 165 Класс Тема: Разнообразный мир линий.
Математика+География
Что представляет с точки зрения
Округление натуральных чисел.
Полярный радиус Земли составляет6357км,а экваториальный6378км.Округлите радиус Земли до разряда тысяч.
Слайд 17Натуральные числа. Математика+История
Индийский правитель, желая отблагодарить мудреца - изобретателя шахмат, предложил
Изобразите фрагмент шахматной доски, впишите в каждую клетку, начиная с первой соответствующее количество зерен, ответьте на вопросы. За какую подсчету клетку количество зерен впервые превысит 1тыс.?100тыс. Превысит ли за 26 клетку 20млн.?
Слайд 18Математика -Физика
Когда мы включаем, выключатель и сразу же вся комната озаряется
Слайд 196 класс: Проценты.Математика+Химия
. Сплав двух металлов олова и цинка 25кг.
Слайд 20Математика-Литература
№7« Читал я где-то
Что царь однажды воинам своим
Велел снести земли по
И гордый холм возвысился
И царь мог с высоты с весельем озирать
И дол, покрытый белыми шатрами, и море, где бежали корабли.» А.С. Пушкин « Скупой рыцарь.» Вопрос какой высоты мог быть такой холм? НА сколько км может увеличиться панорама для наблюдателя, поднявшегося с подножия холма к его вершине?
Слайд 21Прикладные задачи.
Каким может быть наибольший объем бандероли в форме рулона? В
Задача№5Каким может быть наибольший объем бандероли в форме коробки? В правилах почтовой связи находим, что сумма длины, ширины и толщины такой бандероли не должна выходить за 90см, каждое измерение не должно превосходить60см, длина и ширина не могут быть меньше 148 и105 миллиметров соответственно. (Х=300,V=27000см3).
Задача №6 Можно ли послать международной посылкой в форме коробки 5кг пенопласта.?
Слайд 24ЛОТ №1
Самый крупный из представленных сегодня. Отличная комфортабельная яхта с
Слайд 25 Вопросы к лоту №1
Название яхты.
Чтобы узнать слово,
выберите число,
которое
8х – 8 = 0
АЛЕКСАНДРИЯ
0
Большая
медведица
8
ПолярнаяЗвезда
1
Первая яхта « Полярная звезда» была заложена в Балтийском судостроительном заводе
20 мая 1888гв присутствии императорской четы и должностных лиц морского министерства.
Слайд 26Когда была спущена на воду первая яхта?
Какая из записей является уравнением?
2³
а – 3= 7
9х - х²
у ≤ 4
5х < 11
11n³
3у = 85 - у
5² = 25
1891
1890
Слайд 27Лот №4
мадонна».
С каким числом связано
название этой картины?
Слайд 28Решите уравнения :
1
(х+35)-48=24 (х+51)*10=570 21*х+34=349
2
(71-х)+39=45
91-(х+58)=17
х*12+24=96
3
(х-37)+18=47
Х:12+2,4=2,9
(29-х)*100=1400
Выберите наименьший корень.
Ответ: шесть
Слайд 29Лот № 7
Знаете ли вы , что существуют редчайшие почтовые марки
по шахматам. Но на ней не хватает одной фигуры. Предлагаю восстановить ее.
Слайд 30Решите уравнение и подставьте его
корень вместо недостающей координаты. Постройте рисунок.
2х+9=1 (-4;х)
1-2а=11
(m+4,3)-1,7=0,6 (-5;m)
(t-1):0,5=-10 (t;-2)
0,5-k:12=0,25(-4;k)
-5x=0 (x;3)
1,7x-2,8=0,6 (0;x)
-4+0,3n=-2,5 (n;2)
(p-1)+4,8=-1,2(5;p)
y:10-0,15=0,05 (y;-5)
3(x-1,5)+11=0,5 (2;x)
(a-2):0,2+7=2 (a;-2)
0,7x+1,6=2,3 (x;-5)
3-0,7b=6,5 (-2;b)
2-(t+1,8)=1,2(-2;t)
2(y-1)+4,9=-3,1(y;-1)
1,2:n+2,1=1,7(-3;n)
(2+c):0,4+6,5=1,5(c;-3)
1
2
3
1) Ответы:-4,-5,-2,-4,3,0
2) Ответы:2,5,-5,2,-2,1.
3)Ответы :1,-5,-1,-3,-3-4