- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Вписанная окружность
Содержание
- 1. Вписанная окружность
- 2. Какие многоугольники являются описанными?
- 3. Многоугольники, описанные около окружностиМногоугольник называется описанным около
- 4. Свойство описанного около окружности четырехугольникаСуммы противоположных сторон описанного около окружности четырехугольника равны.АВ+СD = BC+AD
- 5. По свойству отрезков касательных АВ + СD
- 6. Признак описанного четырехугольникаЕсли АВ + СD =
- 7. Упражнение 1Ответ: Найдите радиус окружности, вписанной в квадрат со стороной 4.
- 8. Упражнение 2В трапецию, периметр которой равен 56
- 9. Упражнение 3Боковые стороны трапеции, описанной около окружности,
- 10. Упражнение 4Три последовательные стороны четырехугольника, в который
- 11. Упражнение 5Периметр четырехугольника, описанного около окружности, равен
- 12. Упражнение 6Равнобокая трапеция с основаниями а и
- 13. Упражнение 7Около окружности описан четырехугольник АВСD, в котором Найти периметр четырехугольника.
- 14. Домашнее заданиеУчебник Л.С. Атанасян и др.
- 15. Историческая справкаКлавдий Птолемей — греческий географ, картограф,
- 16. Слайд 16
- 17. Спасибо за урок!
Какие многоугольники являются описанными?
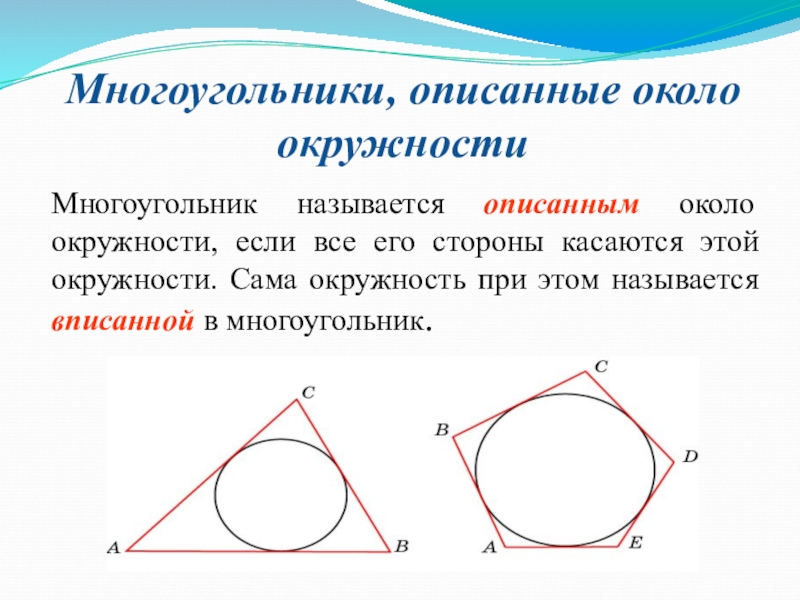
Слайд 3Многоугольники, описанные около окружности
Многоугольник называется описанным около окружности, если все его
стороны касаются этой окружности. Сама окружность при этом называется вписанной в многоугольник.
Слайд 4
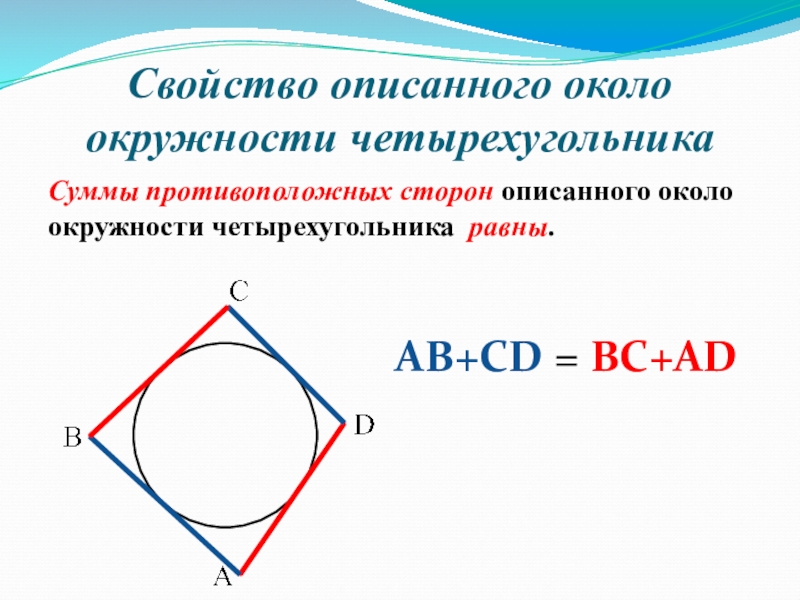
Свойство описанного около окружности четырехугольника
Суммы противоположных сторон описанного около окружности четырехугольника
равны.
АВ+СD = BC+AD
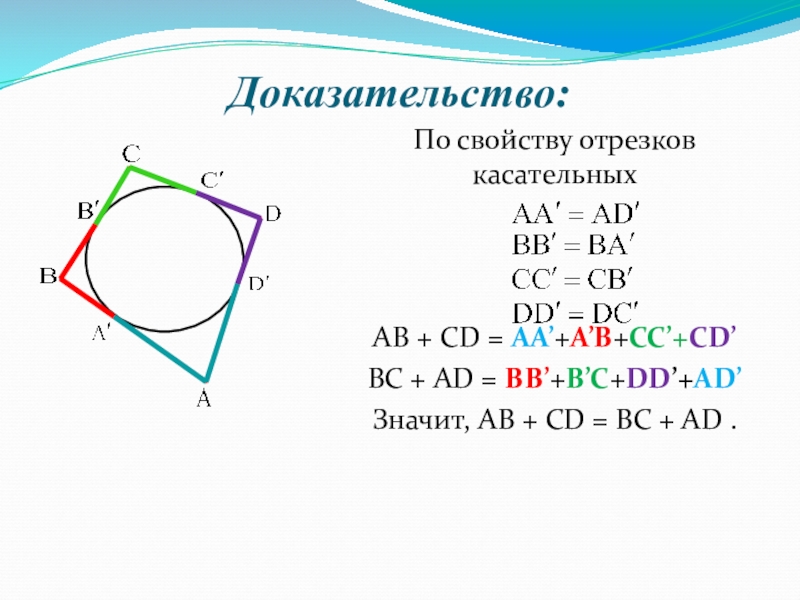
Слайд 5По свойству отрезков касательных
АВ + СD = АА’+А’В+СС’+СD’
BC +
AD = BB’+B’C+DD’+AD’
Значит, АВ + СD = BC + AD .
Значит, АВ + СD = BC + AD .
Доказательство:
Слайд 6Признак описанного четырехугольника
Если АВ + СD = BC + AD, то
в
четырехугольник можно вписать окружность.
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Слайд 8Упражнение 2
В трапецию, периметр которой равен 56 см, вписана окружность. Три
последовательные стороны трапеции относятся как 2:7:12. Найдите стороны трапеции.
Ответ:
Слайд 9Упражнение 3
Боковые стороны трапеции, описанной около окружности, равны 2 см и
4 см. Найдите среднюю линию трапеции.
Ответ:
Слайд 10Упражнение 4
Три последовательные стороны четырехугольника, в который можно вписать окружность, равны
6 см, 8 см и 9 см. Найдите четвертую сторону и периметр этого четырехугольника.
Ответ:
Слайд 11Упражнение 5
Периметр четырехугольника, описанного около окружности, равен 24, две его стороны
равны 5 и 6. Найдите большую из оставшихся сторон.
Ответ:
Слайд 12Упражнение 6
Равнобокая трапеция с основаниями а и b (
)описана около окружности. Найти радиус окружности и косинус угла при большем основании.
Слайд 13Упражнение 7
Около окружности описан четырехугольник АВСD, в котором
Найти периметр четырехугольника.
Слайд 14Домашнее задание
Учебник Л.С. Атанасян и др.
№696, №697, №698, №700
Геометрия.
Дополнительные главы к учебнику: пункт 59 (Теорема Птолемея) разобрать самостоятельно.
Слайд 15Историческая справка
Клавдий Птолемей — греческий географ, картограф, математик, астроном — родился
в Египте, работал главным образом в Александрии.