- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок-презентация Показательные и степенные функции. Их свойства и графики СПО Гаджиева Зулайхат Гапуровна
Содержание
- 1. Урок-презентация Показательные и степенные функции. Их свойства и графики СПО Гаджиева Зулайхат Гапуровна
- 2. Чтобы научиться плавать, надо лезть в воду.пословица
- 3. 45 90 244
- 4. 45 90 244
- 5. 45 90 244
- 6. 45 90 244
- 7. 45 90 244
- 8. 45 90 244
- 9. 45 90 244
- 10. 45 90 244
- 11. 45 90 244
- 12. 45 90 244
- 13. 90 244 45
- 14. 244 90
- 15. 244
- 16. 244
- 17. 244
- 18. 244
- 19. 45 90 244
- 20. 244
- 21. 244
- 22. Слайд 22
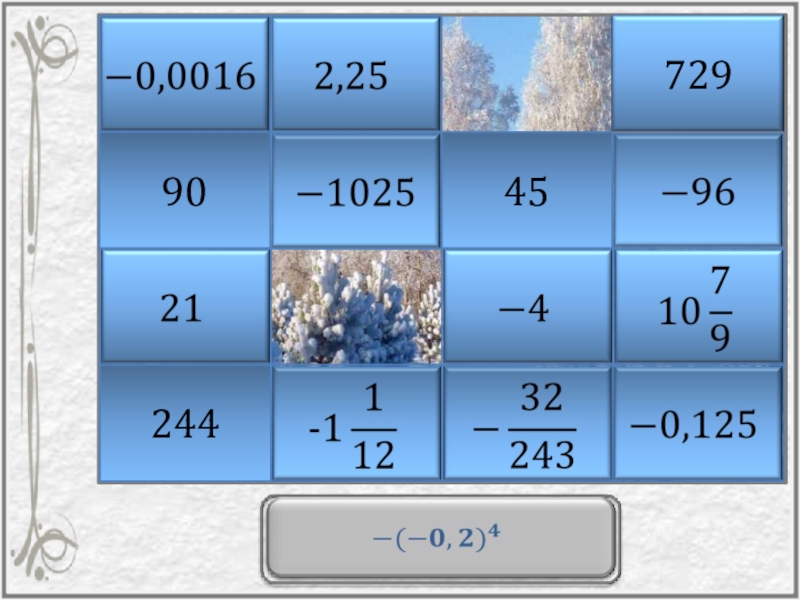
- 23. «Вспомни»Вычислить:
- 24. Урок №22Тема урока: Показательные и степенные функции. Свойства функцииГаджиева З.Г. РАЭК
- 25. Слайд 25
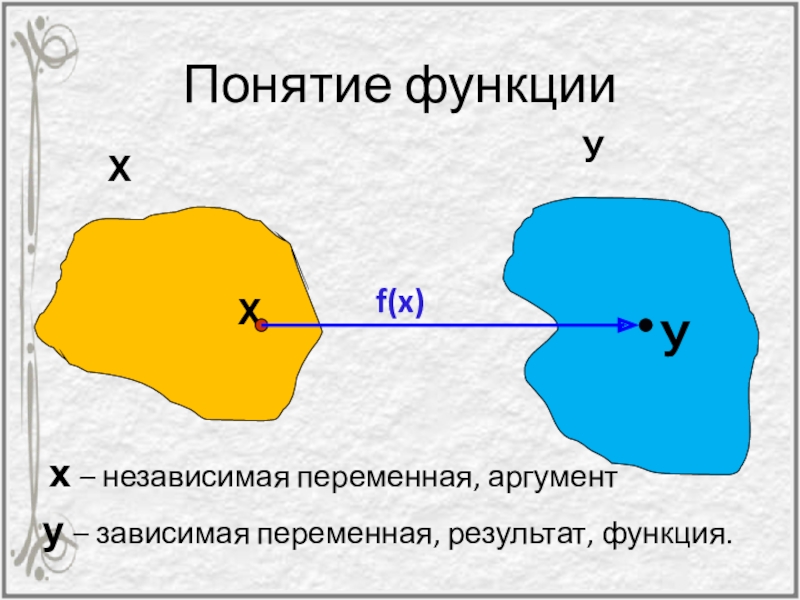
- 26. Понятие функцииХУХУf(x)х – независимая переменная, аргумент у – зависимая переменная, результат, функция.
- 27. Определение функции. Обозначение функции.
- 28. Задание 1. Определите, какая из данных зависимостей
- 29. 1 2 3 4
- 30. ЛИНЕЙНАЯ ФУНКЦИЯ y=kx+b
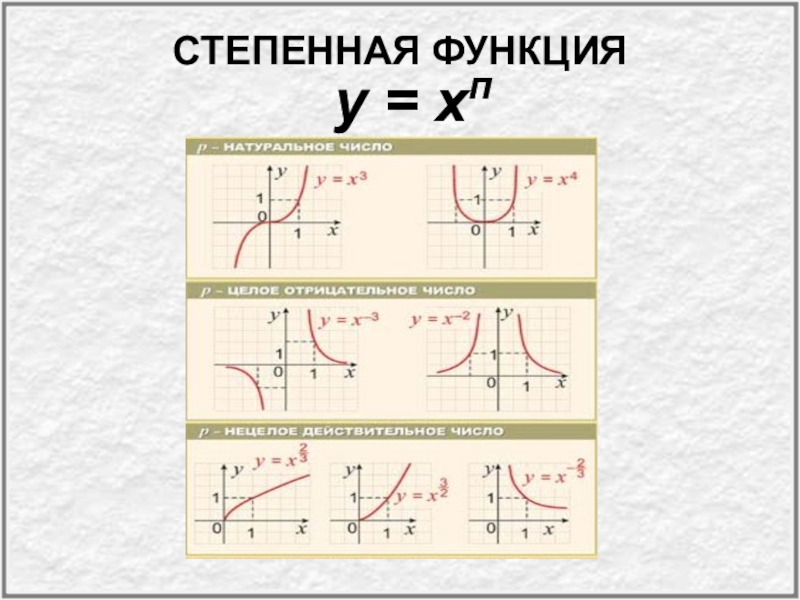
- 31. СТЕПЕННАЯ ФУНКЦИЯ у = хп
- 32. Степенная функцияу = х n Степенью называется выражение вида Здесь а — основание степени, n — показатель степени.аn Показательная функция
- 33. ОпределениеПоказательная функция – это функция вида
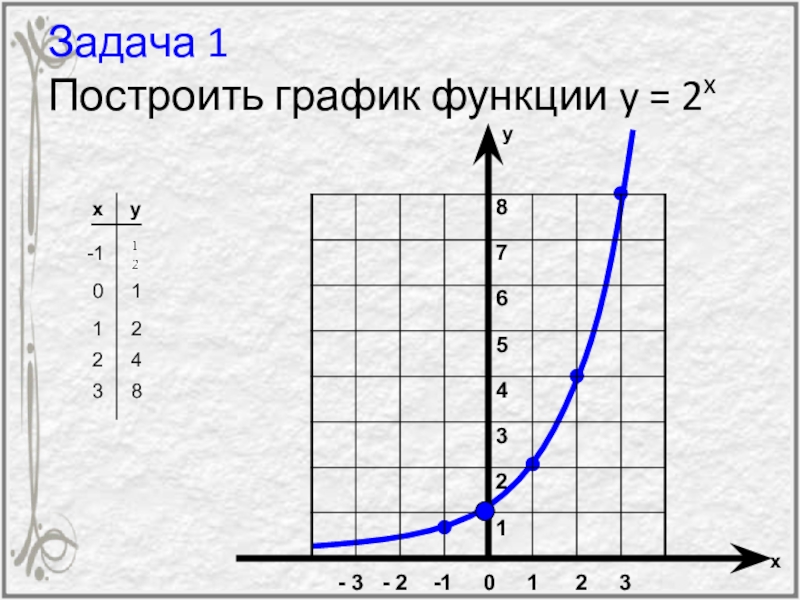
- 34. Задача 1 Построить график функции y
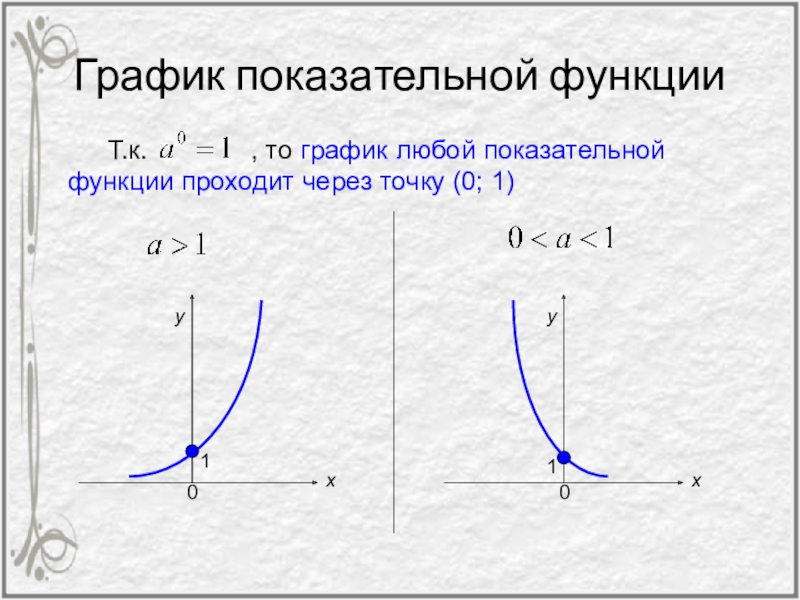
- 35. График показательной функцииТ.к.
- 36. 1) D(аx) = R.2) E(аx)= R+3) Ось ОХ- нет(нулей функции нет)Ось ОУ-(0;1)4) Функция возрастающая.1
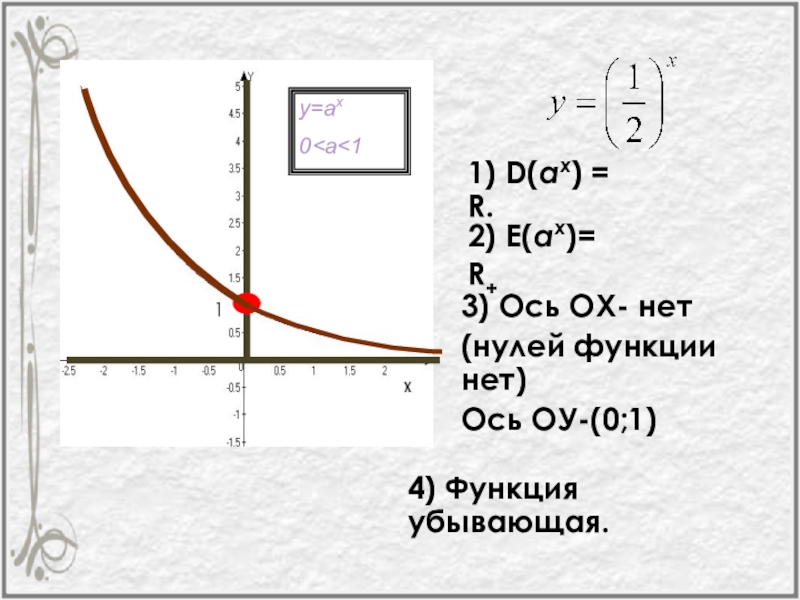
- 37. 1) D(аx) = R.2) E(аx)= R+3) Ось ОХ- нет(нулей функции нет)Ось ОУ-(0;1)4) Функция убывающая.1
- 38. УСТНОВыбрать ту функцию, которая является показательной:;
- 39. Укажите возрастающую функциюУкажите убывающую функцию
- 40. Задача 2 Сравнить числа РешениеОтвет:
- 41. Задача 3 Сравнить число с 1. Решение-5 < 0Ответ:
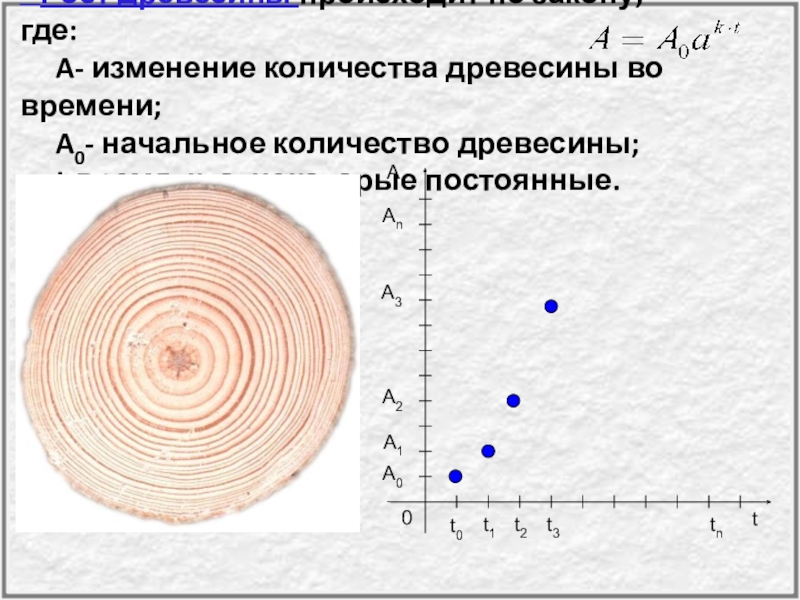
- 42. Рост древесины происходит по
- 43. За какое время t количество древесины А не превышает 1000 м3, если её начальное количество А0 =25 м3.- Как решается эта задача?
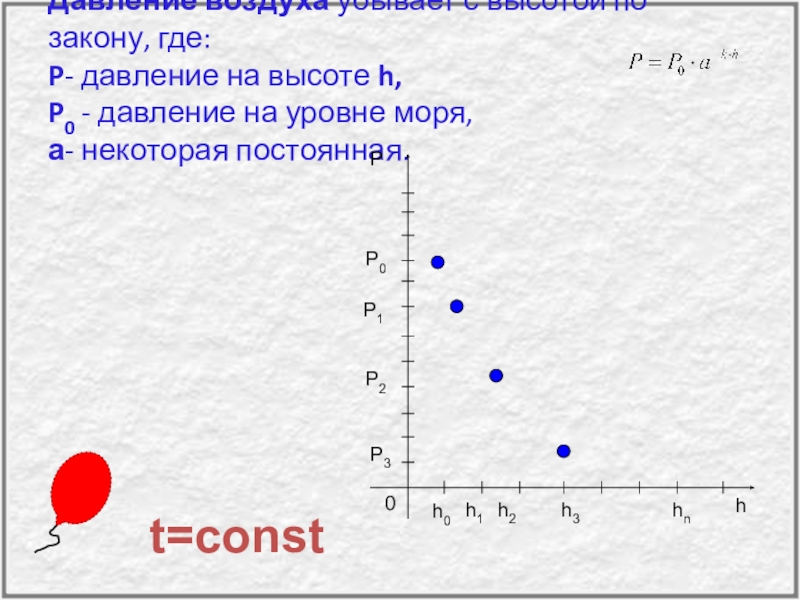
- 44. Давление воздуха убывает с высотой по закону,
- 45. В ходе распада радиоактивного изотопа, его масса
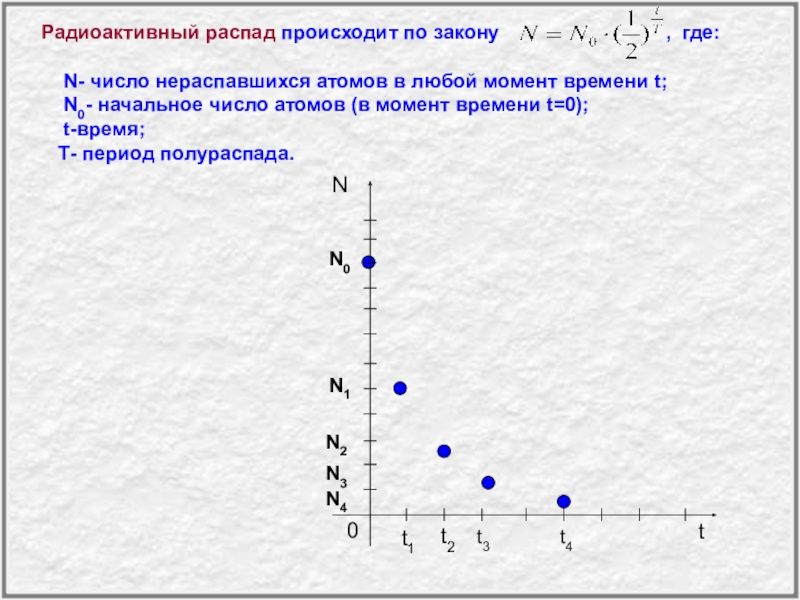
- 46. Радиоактивный распад происходит по закону
- 47. В сосуде находится кусок радиоактивного вещества, имеющего
- 48. Решение
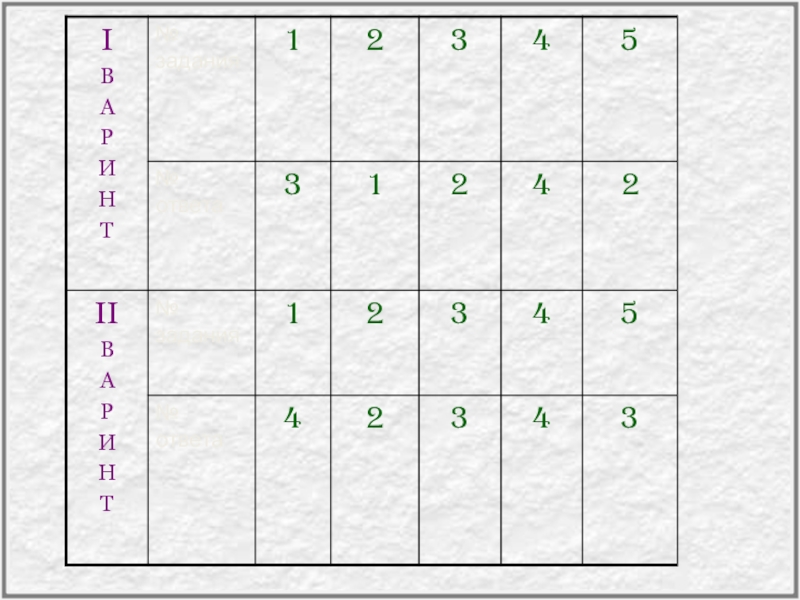
- 49. Самостоятельная работа (тест)
- 50. Слайд 50
- 51. Итог урока: Чем мы с вами
- 52. Спасибо за внимание!Не забывайте готовиться к урокам!
- 53. Решить уравнения:Проверка:1) x = 32) x = -2/33) Корней нет4) ?
- 54. Решая последнее уравнение,мы столкнулись с проблемойзаписи полученного ответа.Прежних знаний для этогоявно недостаточно.
- 55. Выписать свойства логарифмовПрезентация илиСообщение по теме.http://www.myshared.ru/slide/1257252/Богомолов Н.В.
Чтобы научиться плавать, надо лезть в воду.пословица
Слайд 26Понятие функции
Х
У
Х
У
f(x)
х – независимая переменная, аргумент
у – зависимая переменная, результат,
функция.
Слайд 28
Задание 1.
Определите, какая из данных зависимостей является функциональной
1)
x y 2) a q 3) x d 4) n f
Слайд 291 2 3 4 5 6
7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
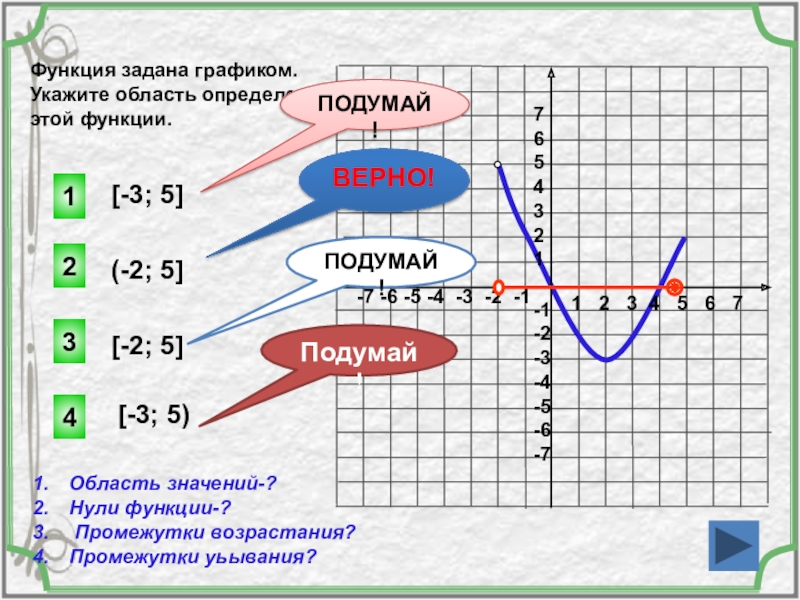
Функция задана графиком.
Укажите область определения
этой функции.
[-3; 5]
[-3; 5)
[-2; 5]
(-2; 5]
2
ВЕРНО!
1
3
4
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
Область значений-?
Нули функции-?
Промежутки возрастания?
Промежутки уьывания?
Слайд 32Степенная функция
у = х n
Степенью называется выражение вида
Здесь а — основание степени,
n — показатель степени.
аn
Показательная
функция
Слайд 33Определение
Показательная функция – это функция вида
,
где x – переменная,
- заданное число, >0, 1.
где x – переменная,
- заданное число, >0, 1.
Примеры:
Слайд 35График показательной функции
Т.к. , то
график любой показательной функции проходит через точку (0; 1)
1
1
х
х
у
у
0
0
Слайд 361) D(аx) = R.
2) E(аx)= R+
3) Ось ОХ- нет
(нулей функции нет)
Ось
ОУ-(0;1)
4) Функция возрастающая.
1
Слайд 371) D(аx) = R.
2) E(аx)= R+
3) Ось ОХ- нет
(нулей функции нет)
Ось
ОУ-(0;1)
4) Функция убывающая.
1
Слайд 42 Рост древесины происходит по закону, где:
A- изменение количества древесины во времени;
A0- начальное количество древесины;
t-время, к, а- некоторые постоянные.
Слайд 43
За какое время t количество древесины А не превышает
1000 м3, если её начальное количество А0 =25
м3.
- Как решается эта задача?
- Как решается эта задача?
Слайд 44Давление воздуха убывает с высотой по закону, где: P- давление на
высоте h,
P0 - давление на уровне моря,
а- некоторая постоянная.
t=const
Слайд 45В ходе распада радиоактивного изотопа, его масса уменьшается по закону
,
где – начальная масса изотопа,t (мин) – прошедшее от начального момен‐ та время, т– период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени мг изотопа , период полураспада которого мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
Слайд 46 Радиоактивный распад происходит по закону
, где:
N- число нераспавшихся атомов в любой момент времени t; N0- начальное число атомов (в момент времени t=0); t-время;
Т- период полураспада.
N- число нераспавшихся атомов в любой момент времени t; N0- начальное число атомов (в момент времени t=0); t-время;
Т- период полураспада.
N3
N4
t4
N0
t3
N2
N1
Слайд 47В сосуде находится кусок радиоактивного вещества, имеющего массу N₀=20г. Период полураспада
T=2ч. Сколько граммов N радиактивного вещества разложится в течении 12 часов.
Слайд 48Решение
12
N = 20 ∙ (1/2) 2 = 20 ∙ (1/2) 6 =
20 ∙ (1/64) = 20 / 64 = 5 / 16 =
1/ 3 г.
То есть за 12 часов смогло разложиться только 1/ 3 грамма вещества.
N = 20 ∙ (1/2) 2 = 20 ∙ (1/2) 6 =
20 ∙ (1/64) = 20 / 64 = 5 / 16 =
1/ 3 г.
То есть за 12 часов смогло разложиться только 1/ 3 грамма вещества.
Слайд 51Итог урока: Чем мы с вами занимались на уроке? Что нового
вы узнали?
Что понравилось?
что не понравилось?
Желаю вам успешно справиться с домашней работой.
Слайд 52Спасибо за внимание!
Не забывайте готовиться к урокам!
Тема урока: Логарифмы
и их свойства . Десятичные, натуральные логарифмы.
План урока:
Определение логарифма
Свойства логарифмов
Вычисление логарифмов
План урока:
Определение логарифма
Свойства логарифмов
Вычисление логарифмов
Слайд 54Решая последнее уравнение,
мы столкнулись с проблемой
записи полученного ответа.
Прежних знаний для этого
явно
недостаточно.
Слайд 55Выписать свойства
логарифмов
Презентация или
Сообщение по теме.
http://www.myshared.ru/slide/1257252/
Богомолов Н.В. Практические задания по математике.
ГЛ. 4 Стр.58-64
