привычным, привычное приятным!»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок по теме: Квадратичная функция, её свойства и график
Содержание
- 1. Урок по теме: Квадратичная функция, её свойства и график
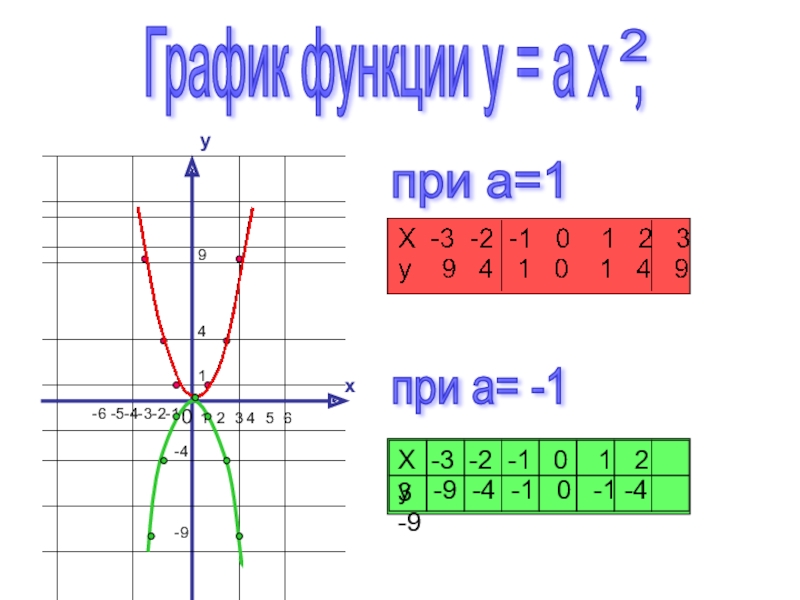
- 2. yx0График функции y = a x ,2при a=1при a= -11 2 3 4 5 6-6 -5-4-3-2-1149-9-4
- 3. Преобразование графика квадратичной функции
- 4. Построение графиков функций у=х2 и у=х2+m.
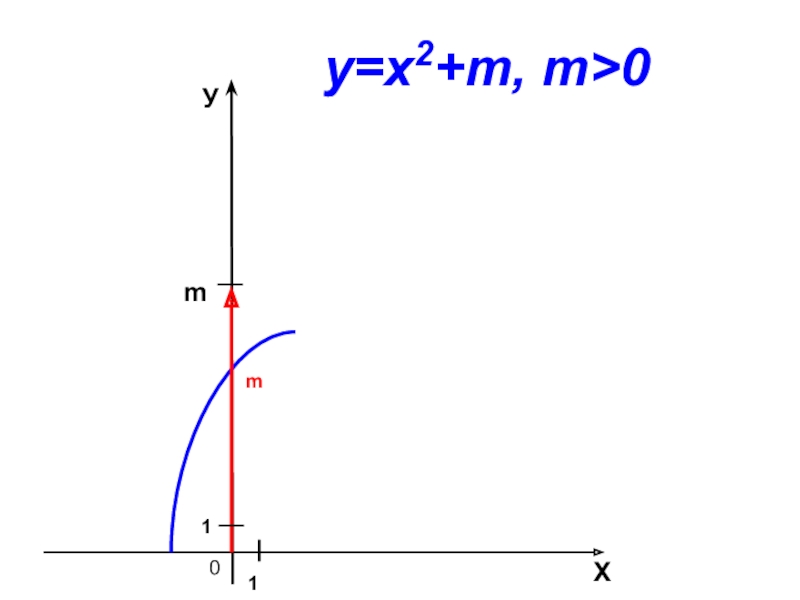
- 5. 0mХУ11у=х2+m, m>0
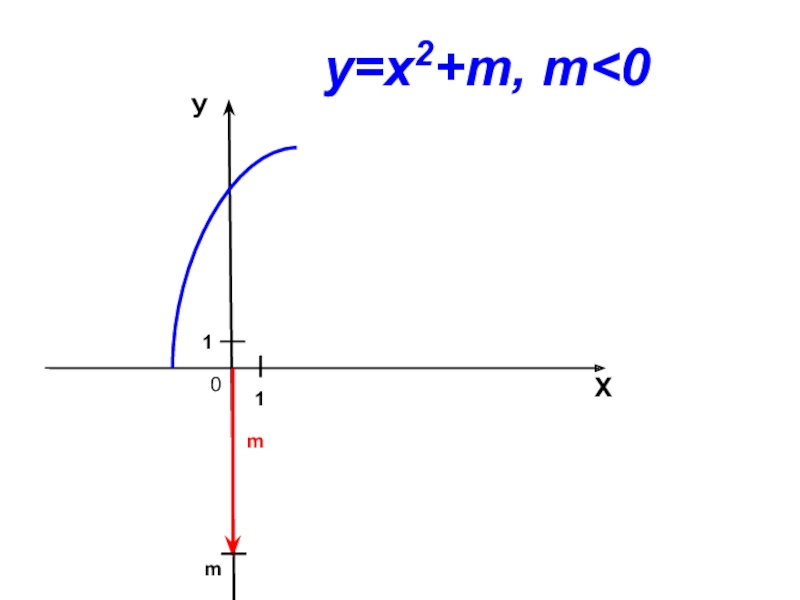
- 6. 0ХУ11mу=х2+m, m
- 7. Постройте в одной координатной плоскости
- 8. Построение графиков функций у=х2 и у=(х+l)2.
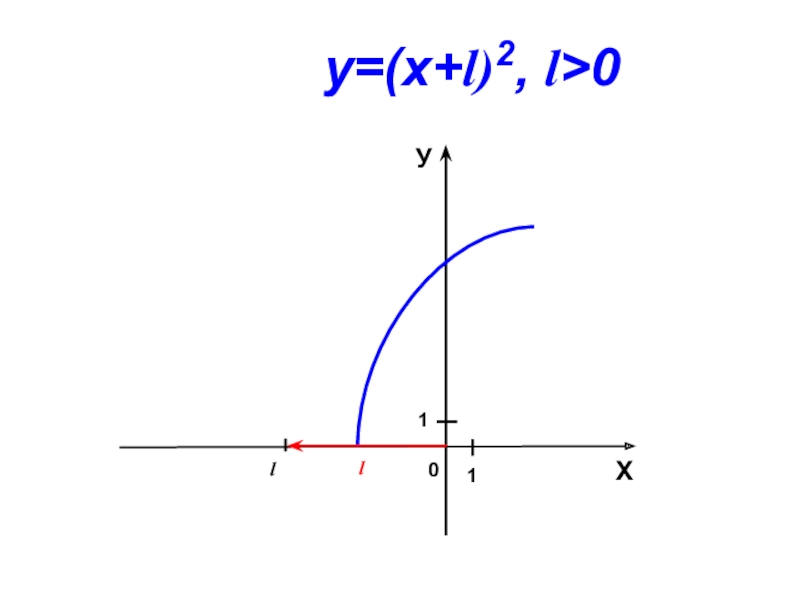
- 9. 0lХУ11у=(х+l)2, l>0
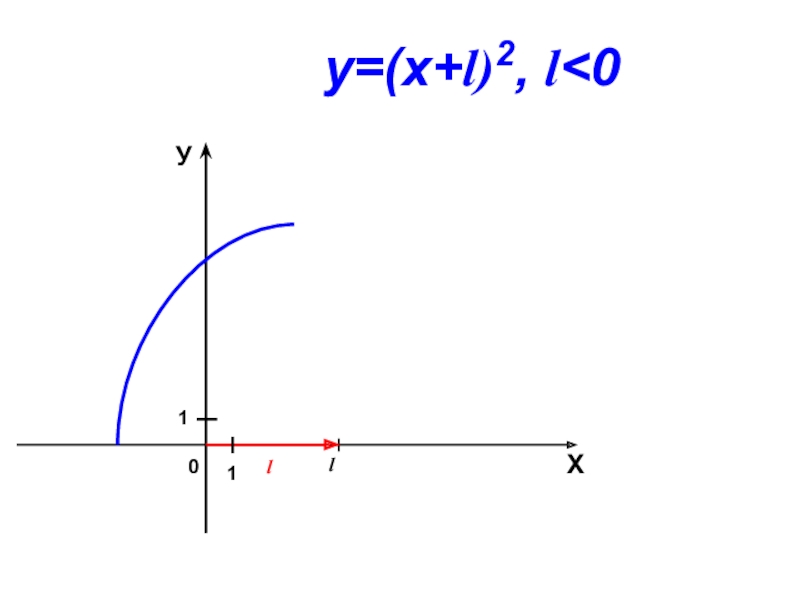
- 10. 0lХУ11у=(х+l)2, l
- 11. Постройте в одной координатной плоскости
- 12. Найти координаты вершины параболы: У=2(х-4)² +5У=-6(х-1)²У = -х²+12У= х²+4У= (х+7)² - 9У=6 х² (4;5)(1;0)(0;12)(0;4)(-7;-9)(0;0)
- 13. График квадратичной функции, его свойства
- 14. Квадратичной функцией называется функция, которую можно задать
- 15. Графиком квадратичной функции является парабола, ветви которой
- 16. Определить координату вершины параболы по формулам:Отметить эту
- 17. Постройте график функции у=2х²+4х-6, опишите его свойства
- 18. ХУ11-223-11. D(y)= R2. у=0, если х=1; -33.
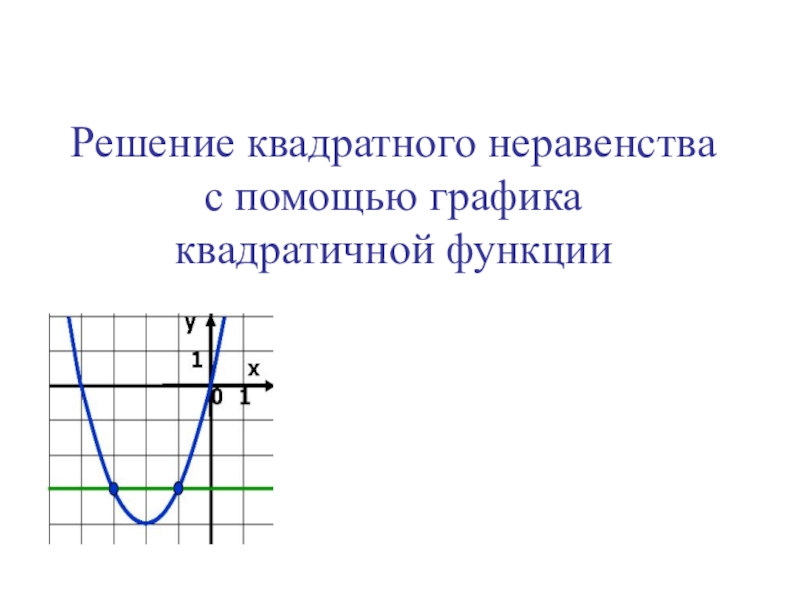
- 19. Решение квадратного неравенства с помощью графика квадратичной функции
- 20. Определение: Неравенство, левая часть которого есть многочлен
- 21. Какие из неравенств вы бы назвали
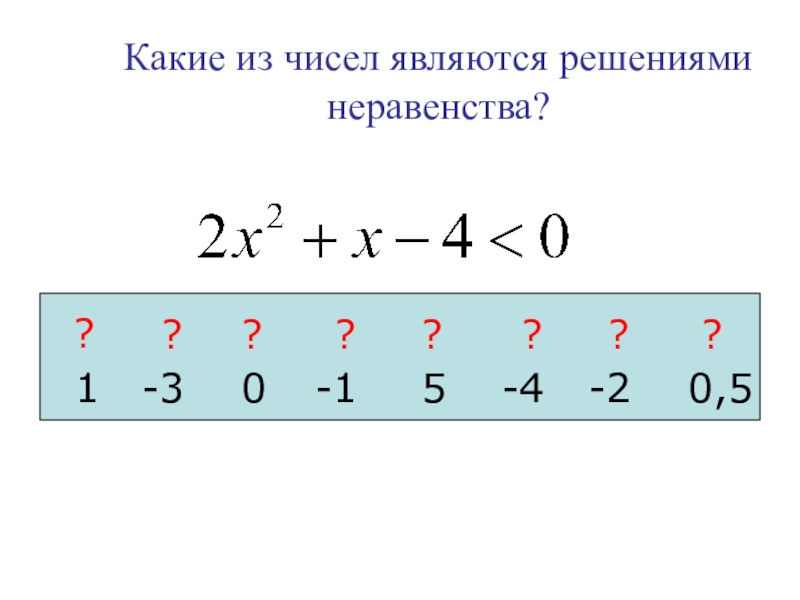
- 22. Какие из чисел являются решениями неравенства?1-30-15-4-20,5????????
- 23. Назовите число корней уравнения
- 24. Назовите промежутки знакопостоянства функции, если её график расположен указанным образом:Ι вариант.ΙІ вариант.вбаавб
- 25. Назовите промежутки знакопостоянства функции, если её график
- 26. Назовите промежутки знакопостоянства функции, если её график
- 27. Назовите промежутки знакопостоянства функции, если её график
- 28. Алгоритм решения неравенств второй степени с одной переменной5х2+9х-20 (ax2+bx+c0 (y
- 29. Алгоритм решения неравенств второй степени с одной переменной5х2+9х-20 (ax2+bx+c0 (y0 (y
- 30. Алгоритм решения неравенств второй степени с одной переменной5х2+9х-20 (ax2+bx+c0 (y0 (y
- 31. В таблице 1 найдите верное решение неравенства
- 32. В таблице 1 найдите верное решение неравенства
- 33. В таблице 1 найдите верное решение неравенства
- 34. В таблице 1 найдите верное решение неравенства
- 35. Итог урока При решении данных заданий нам
- 36. Незаконченное предложение Задание: закончить
- 37. Домашнее заданиеУчебник №142; №190
- 38. Слайд 38
yx0График функции y = a x ,2при a=1при a= -11 2 3 4 5 6-6 -5-4-3-2-1149-9-4
Слайд 12Найти координаты вершины параболы:
У=2(х-4)² +5
У=-6(х-1)²
У = -х²+12
У= х²+4
У= (х+7)² -
9
У=6 х²
(4;5)
(1;0)
(0;12)
(0;4)
(-7;-9)
(0;0)
Слайд 14Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где
х - независимая переменная, a, b и с -некоторые числа (причём а≠0).
Например: у = 5х²+6х+3,
у = -7х²+8х-2,
у = 0,8х²+5,
у = ¾х²-8х,
у = -12х²
квадратичные функции
Слайд 15Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а>0) или
вниз (если а<0).
у=2х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а>0).
у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а<0).
у
0
х
у
0
х
Слайд 16Определить координату вершины параболы по формулам:
Отметить эту точку на координатной плоскости.
Через вершину параболы начертить ось симметрии параболы
Найти нули функции и 0тметить их на числовой прямой
Найти координаты двух дополнительных точек и симметричных им
Провести кривую параболы.
Найти нули функции и 0тметить их на числовой прямой
Найти координаты двух дополнительных точек и симметричных им
Провести кривую параболы.
Алгоритм решения
Слайд 18Х
У
1
1
-2
2
3
-1
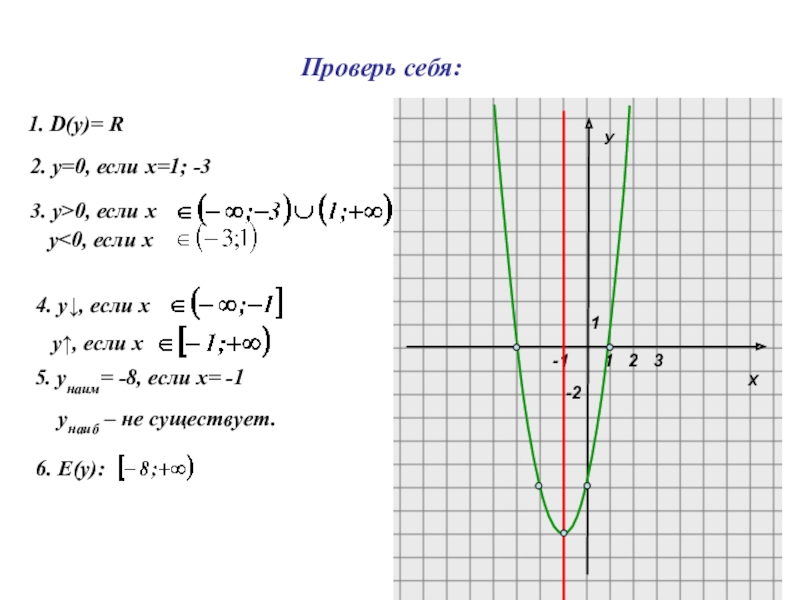
1. D(y)= R
2. у=0, если х=1; -3
3. у>0, если х
4. у↓,
если х
у↑, если х
5. унаим= -8, если х= -1
унаиб – не существует.
6. Е(y):
Проверь себя:
у<0, если х
Слайд 20Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая-
нуль, называется неравенством второй степени.
Все квадратные неравенства могут быть приведены к одному из следующих видов:
1) ах2+bx+c>0; 2) ах2+bx+c<0;
3) ах2+bx+c≥0; 4) ах2+bx+c≤0.
Слайд 21 Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х
2-13х>0; 2) x 2-3x-14>0;
3) (5+x)(x-4)>7; 4) ;
5)
6) 8x2 >0; 7) (x-5)2 -25>0;
3) (5+x)(x-4)>7; 4) ;
5)
6) 8x2 >0; 7) (x-5)2 -25>0;
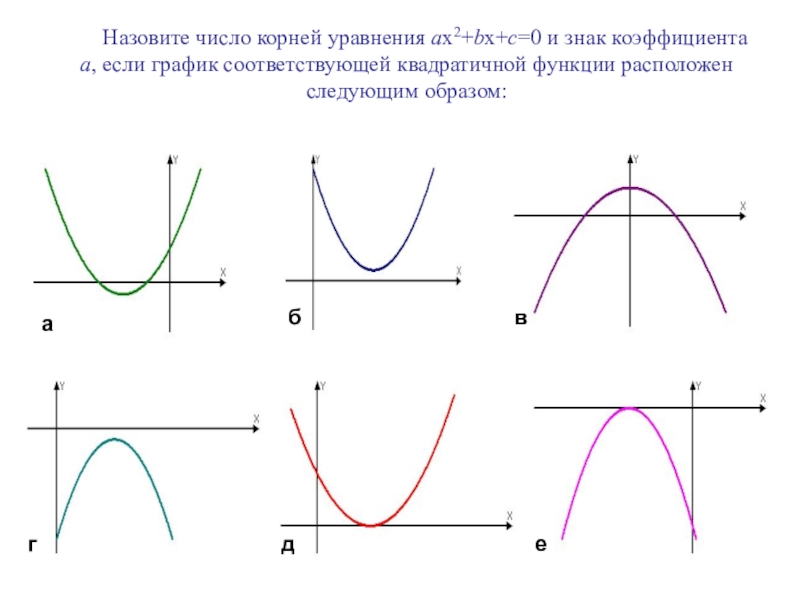
Слайд 23 Назовите число корней уравнения ax2+bx+c=0 и знак коэффициента
а, если график соответствующей квадратичной функции расположен следующим образом:
е
а
б
в
г
д
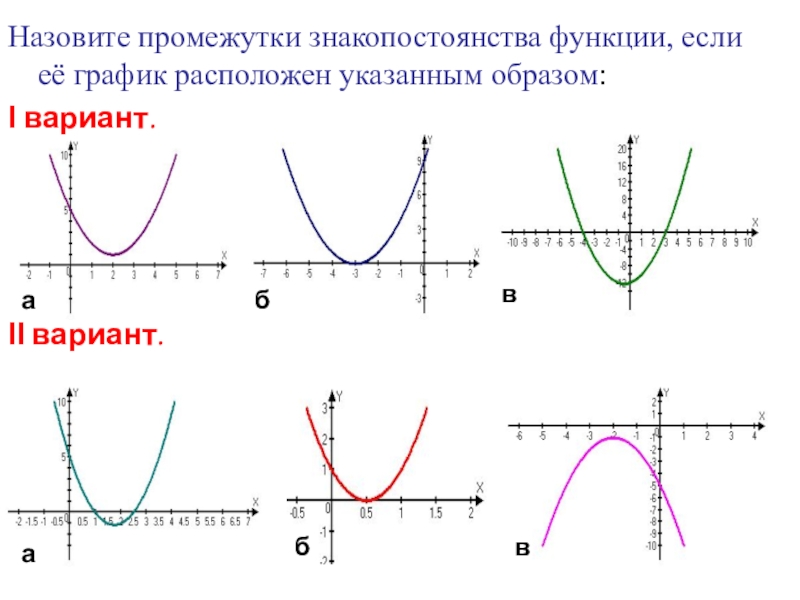
Слайд 24Назовите промежутки знакопостоянства функции, если её график расположен указанным образом:
Ι вариант.
ΙІ
вариант.
в
б
а
а
в
б
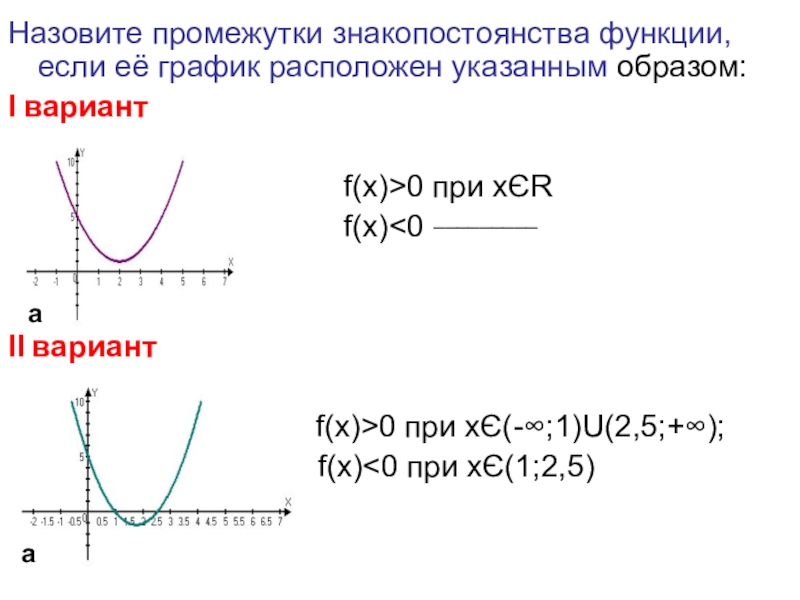
Слайд 25Назовите промежутки знакопостоянства функции, если её график расположен указанным образом:
Ι вариант
f(x)>0 при xЄR
f(x)<0 _________
ΙІ вариант
f(x)>0 при xЄ(-∞;1)U(2,5;+∞);
f(x)<0 при xЄ(1;2,5)
f(x)<0 _________
ΙІ вариант
f(x)>0 при xЄ(-∞;1)U(2,5;+∞);
f(x)<0 при xЄ(1;2,5)
а
а
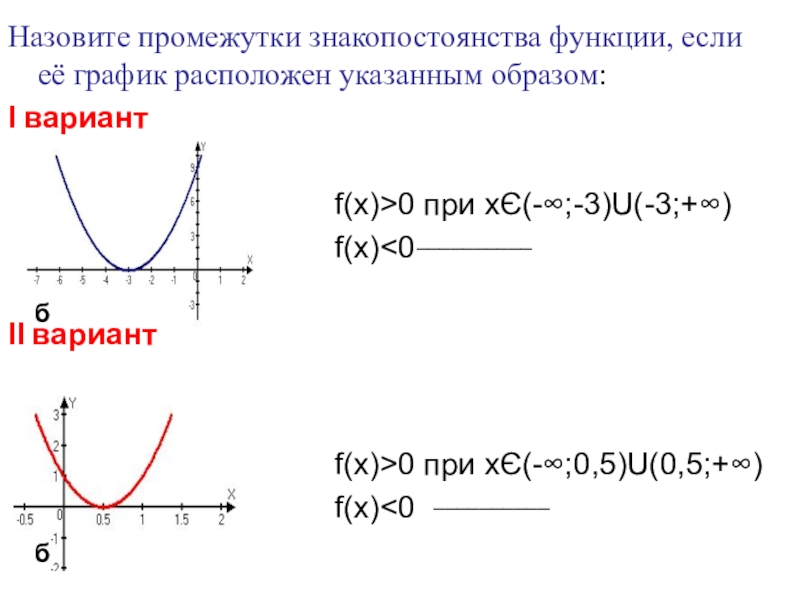
Слайд 26Назовите промежутки знакопостоянства функции, если её график расположен указанным образом:
Ι вариант
f(x)>0 при xЄ(-∞;-3)U(-3;+∞)
f(x)<0__________
ΙІ вариант
f(x)>0 при xЄ(-∞;0,5)U(0,5;+∞)
f(x)<0 __________
б
б
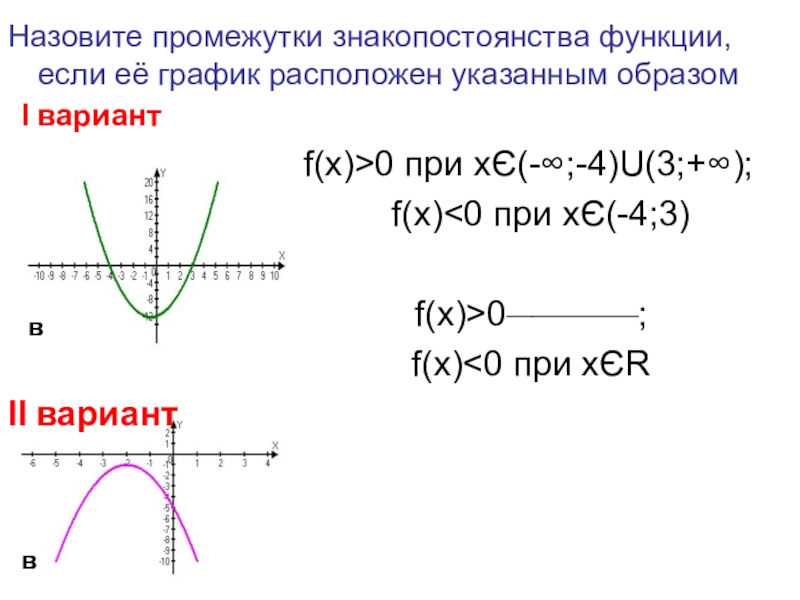
Слайд 27Назовите промежутки знакопостоянства функции, если её график расположен указанным образом
Ι вариант
f(x)>0 при xЄ(-∞;-4)U(3;+∞);
f(x)<0 при xЄ(-4;3)
f(x)>0__________;
f(x)<0 при xЄR
ΙІ вариант
f(x)>0 при xЄ(-∞;-4)U(3;+∞);
f(x)<0 при xЄ(-4;3)
f(x)>0__________;
f(x)<0 при xЄR
ΙІ вариант
в
в
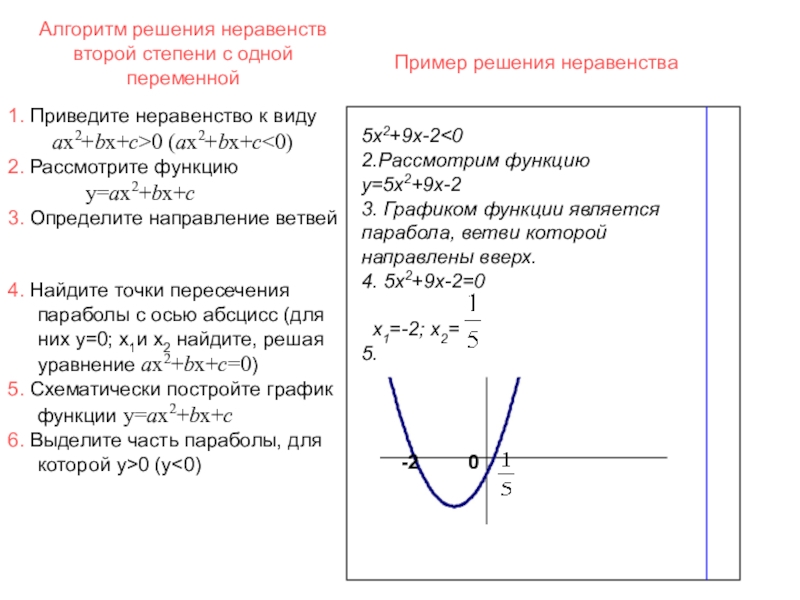
Слайд 28Алгоритм решения неравенств второй степени с одной переменной
5х2+9х-2
функции является парабола, ветви которой направлены вверх.
4. 5х2+9х-2=0
х1=-2; х2=
5.
4. 5х2+9х-2=0
х1=-2; х2=
5.
-2
0
1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей
4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
5. Схематически постройте график функции y=ax2+bx+c
6. Выделите часть параболы, для которой y>0 (y<0)
Пример решения неравенства
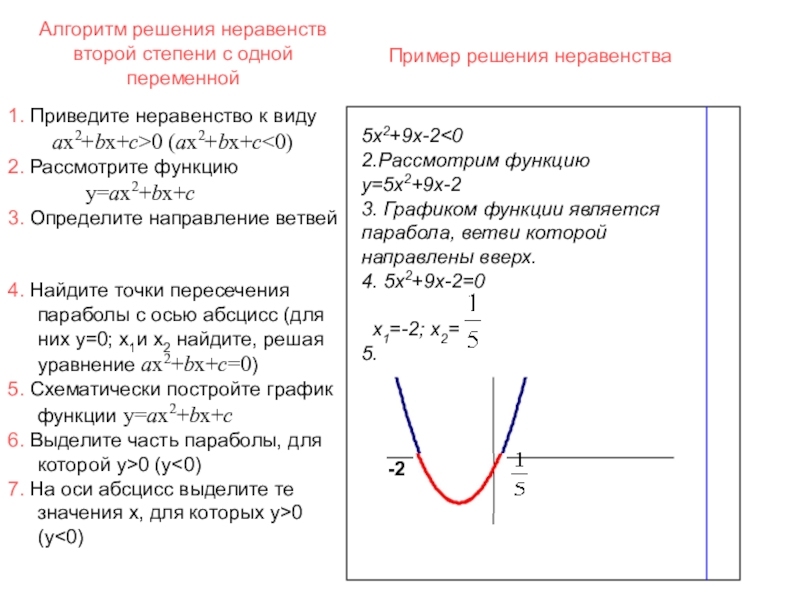
Слайд 29Алгоритм решения неравенств второй степени с одной переменной
5х2+9х-2
функции является парабола, ветви которой направлены вверх.
4. 5х2+9х-2=0
х1=-2; х2=
5.
4. 5х2+9х-2=0
х1=-2; х2=
5.
-2
0
1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей
4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
5. Схематически постройте график функции y=ax2+bx+c
6. Выделите часть параболы, для которой y>0 (y<0)
7. На оси абсцисс выделите те значения х, для которых y>0 (y<0)
Пример решения неравенства
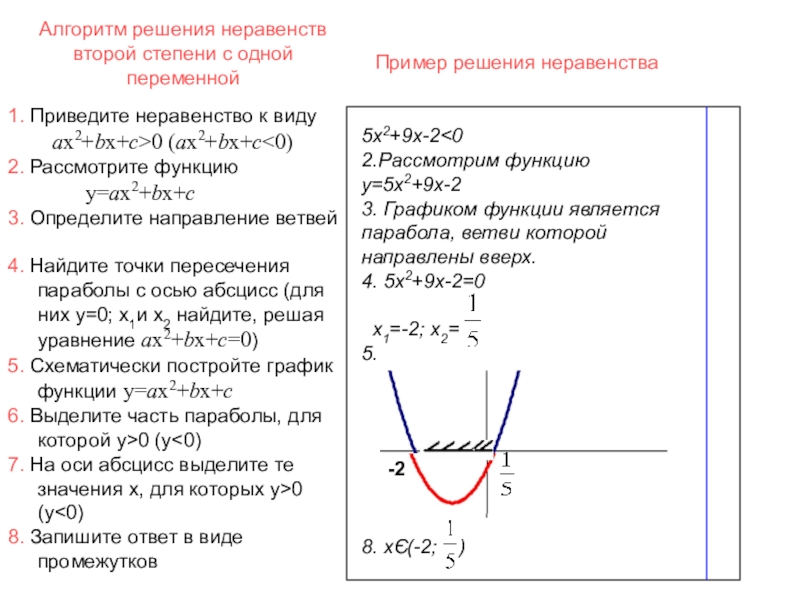
Слайд 30Алгоритм решения неравенств второй степени с одной переменной
5х2+9х-2
функции является парабола, ветви которой направлены вверх.
4. 5х2+9х-2=0
х1=-2; х2=
5.
8. хЄ(-2; )
4. 5х2+9х-2=0
х1=-2; х2=
5.
8. хЄ(-2; )
-2
0
1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей
4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
5. Схематически постройте график функции y=ax2+bx+c
6. Выделите часть параболы, для которой y>0 (y<0)
7. На оси абсцисс выделите те значения х, для которых y>0 (y<0)
8. Запишите ответ в виде промежутков
Пример решения неравенства
Слайд 31В таблице 1 найдите верное решение неравенства 1, в таблице 2
- решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2
Слайд 32В таблице 1 найдите верное решение неравенства 1, в таблице 2-
решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2
Слайд 33В таблице 1 найдите верное решение неравенства 1, в таблице 2-
решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2
Слайд 34В таблице 1 найдите верное решение неравенства 1, в таблице 2-
решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2
Слайд 35Итог урока
При решении данных заданий нам удалось систематизировать знания о
применении квадратичной функции. Математика- это содержательное, увлекательное и доступное поле деятельности, дающее ученику богатую пищу для ума. Свойства квадратичной функции лежат в основе решения квадратных неравенств. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростьюv0, находится в момент времени t на расстоянии
s(t)=-q\2t2+v0t
от земной поверхности (здесь q- ускорение силы тяжести);
количество тепла Q, выделяемое при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой
Q=RI2.
Знания свойств квадратичной функции позволяют рассчитать дальность полета тела, брошенного вертикально вверх или под некоторым углом. Этим пользуются в оборонной промышленности.
s(t)=-q\2t2+v0t
от земной поверхности (здесь q- ускорение силы тяжести);
количество тепла Q, выделяемое при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой
Q=RI2.
Знания свойств квадратичной функции позволяют рассчитать дальность полета тела, брошенного вертикально вверх или под некоторым углом. Этим пользуются в оборонной промышленности.
Слайд 36Незаконченное предложение
Задание: закончить одно из трех предложений, которое больше
других соответствует вашему состоянию.
“Выполнять задания и решать задачи мне трудно, так как …”
“Выполнять задания и решать задачи мне легко, так как …”
“Выполнять задания и решать задачи для меня занятие приятное и интересное, потому что…”
“Выполнять задания и решать задачи мне трудно, так как …”
“Выполнять задания и решать задачи мне легко, так как …”
“Выполнять задания и решать задачи для меня занятие приятное и интересное, потому что…”
