- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок по математике для 5 класса по теме Функции, их свойства и графики
Содержание
- 1. Урок по математике для 5 класса по теме Функции, их свойства и графики
- 2. Числовой функцией называется соответствие (зависимость), при котором
- 3. 1. Функция , т.к. каждому значению переменной
- 4. Способы задания функций- Аналитический (с помощью формулы) - Графический- Табличный- Описательный (словесное описание)Сила равна скорости изменения импульса
- 5. График функции Графиком функции f называют
- 6. 1. Область определения2. Область значений3. Нули функции4.
- 7. 4. ЧетностьЧетная функцияНечетная функцияФункция y = f(x)
- 8. Исследуйте на четность функцию, график которой изображен на рисункеx0yx0yx0yРис. 1Рис.2Рис. 3НечетнаяЧетнаяНи четная, ни нечетная
- 9. АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИy = ax2+bx+cОпределить
- 10. xy = x2 – 4x – 2
- 11. Древняя китайская мудрость Скажи мне -
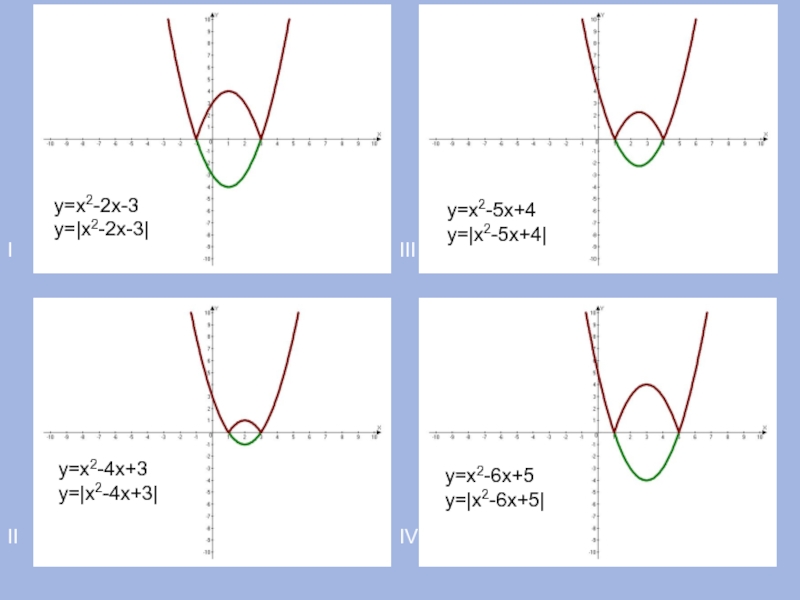
- 12. IIIIIIIVу=х2-2х-3у=|х2-2х-3|у=х2-4х+3у=|х2-4х+3|у=х2-5х+4у=|х2-5х+4|у=х2-6х+5у=|х2-6х+5|
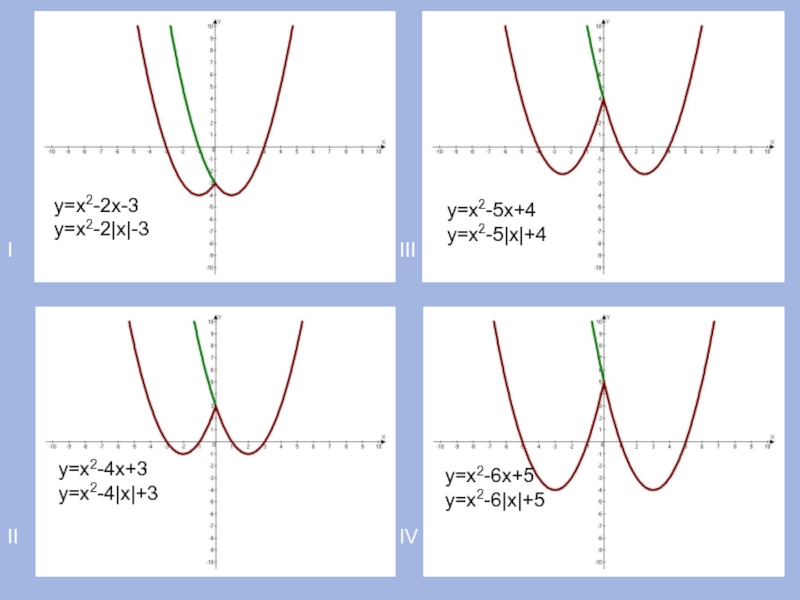
- 13. IIIIIIIVу=х2-2х-3у=х2-2|х|-3у=х2-4х+3у=х2-4|х|+3у=х2-5х+4у=х2-5|х|+4у=х2-6х+5у=х2-6|х|+5
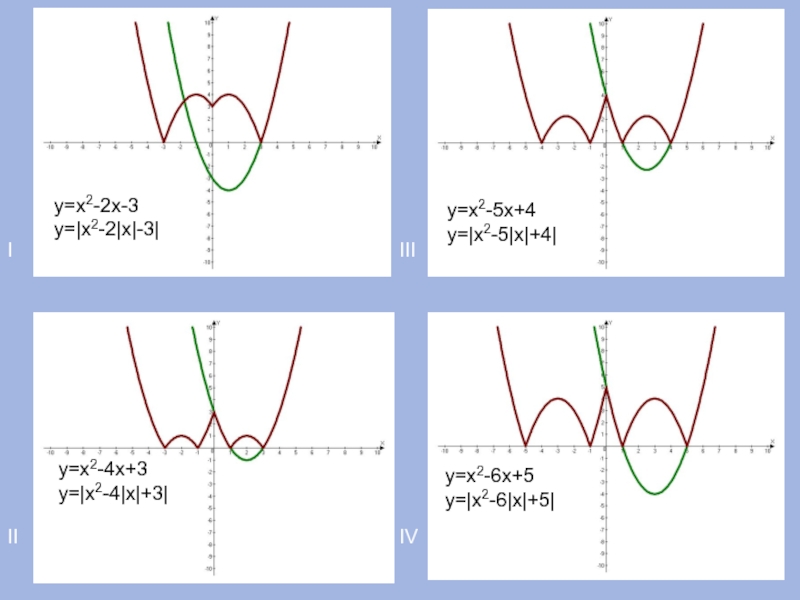
- 14. IIIIIIIVу=х2-2х-3у=|х2-2|х|-3|у=х2-4х+3у=|х2-4|х|+3|у=х2-5х+4у=|х2-5|х|+4|у=х2-6х+5у=|х2-6|х|+5|
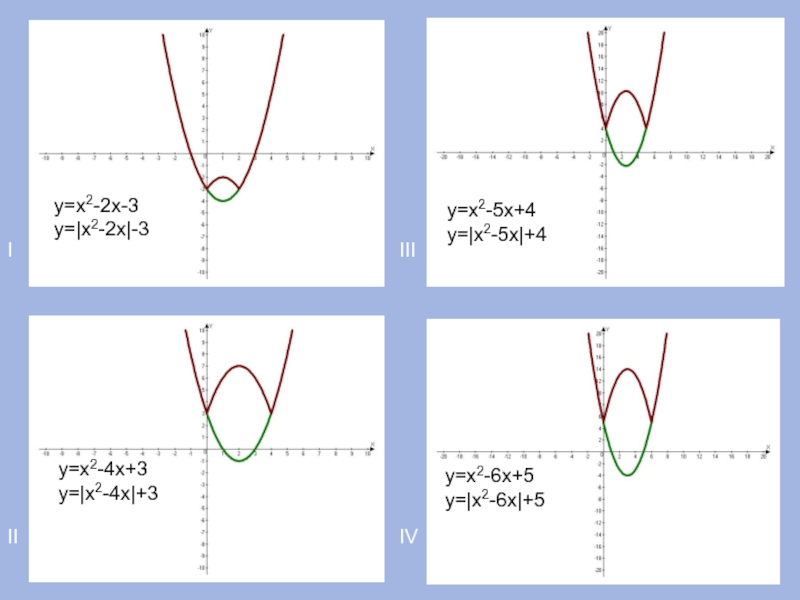
- 15. IIIIIIIVу=х2-2х-3у=|х2-2х|-3у=х2-4х+3у=|х2-4х|+3у=х2-5х+4у=|х2-5х|+4у=х2-6х+5у=|х2-6х|+5
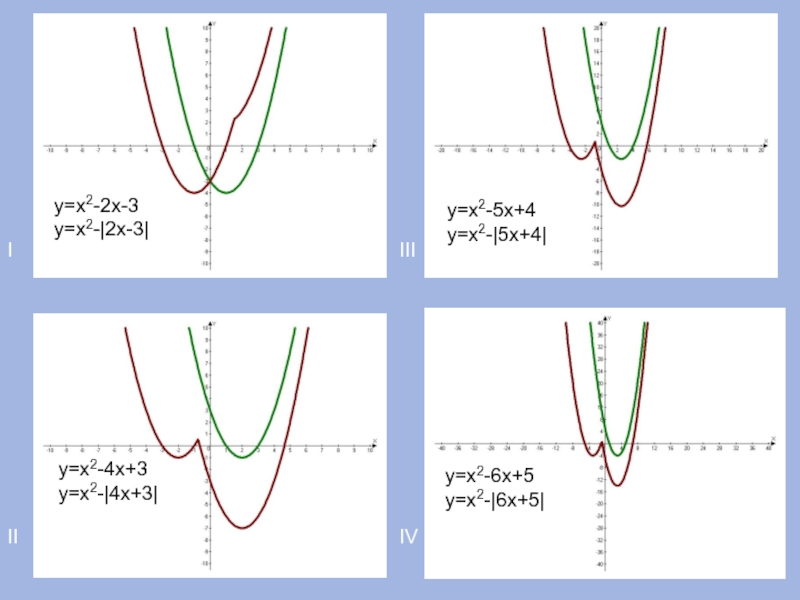
- 16. IIIIIIIVу=х2-2х-3у=х2-|2х-3|у=х2-4х+3у=х2-|4х+3|у=х2-5х+4у=х2-|5х+4|у=х2-6х+5у=х2-|6х+5|
- 17. Тест «Квадратичная функция»
- 18. Домашняя работа (по вариантам)
Слайд 2Числовой функцией называется соответствие (зависимость), при котором каждому значению одной переменной
Обозначают латинскими (иногда греческими) буквами : f, q, h, y, p и т.д.
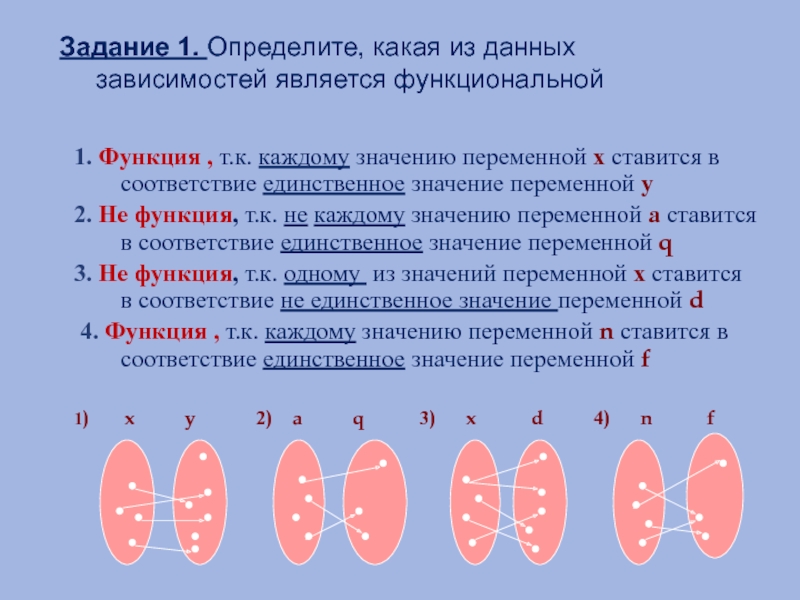
Слайд 31. Функция , т.к. каждому значению переменной х ставится в соответствие
2. Не функция, т.к. не каждому значению переменной а ставится в соответствие единственное значение переменной q
3. Не функция, т.к. одному из значений переменной х ставится в соответствие не единственное значение переменной d
4. Функция , т.к. каждому значению переменной n ставится в соответствие единственное значение переменной f
1) x y 2) a q 3) x d 4) n f
Задание 1. Определите, какая из данных зависимостей является функциональной
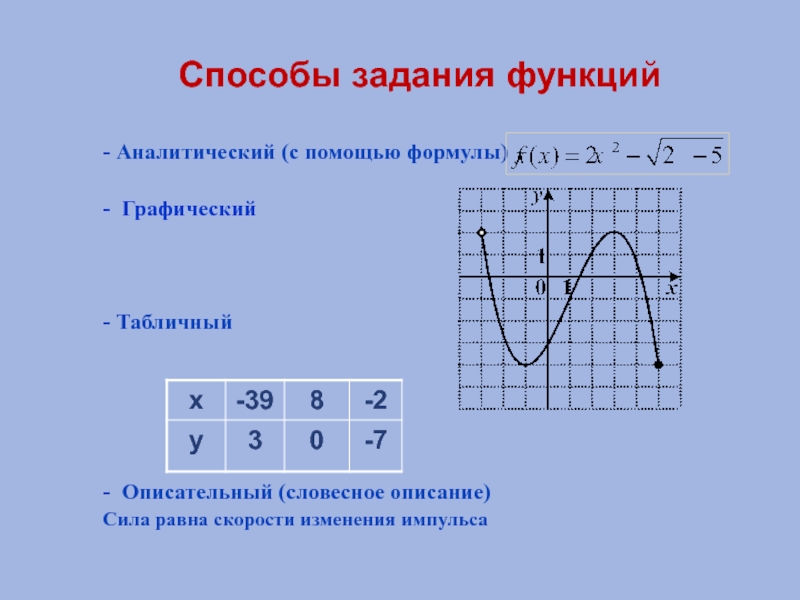
Слайд 4Способы задания функций
- Аналитический (с помощью формулы)
- Графический
- Табличный
- Описательный (словесное
Сила равна скорости изменения импульса
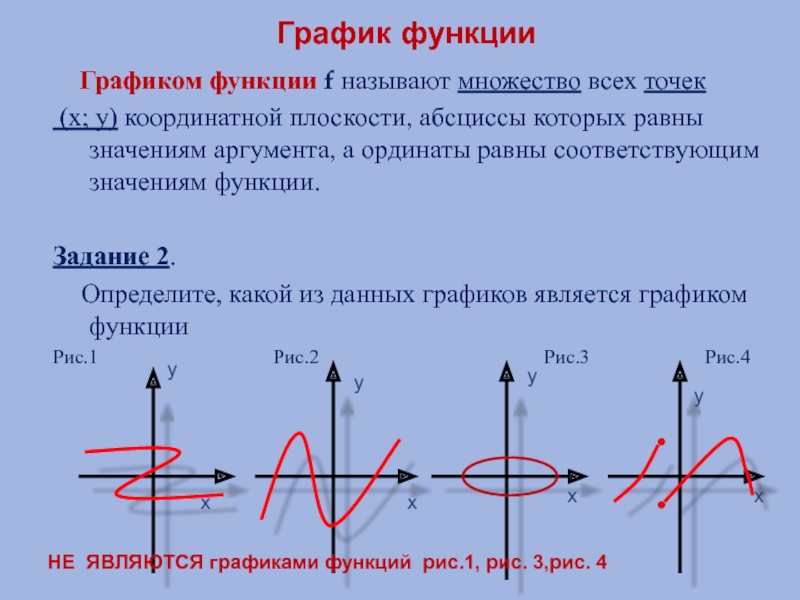
Слайд 5График функции
Графиком функции f называют множество всех точек
Задание 2.
Определите, какой из данных графиков является графиком функции
Рис.1 Рис.2 Рис.3 Рис.4
у
у
у
у
х
х
х
х
НЕ ЯВЛЯЮТСЯ графиками функций рис.1, рис. 3,рис. 4
Слайд 61. Область определения
2. Область значений
3. Нули функции
4. Четность
5. Промежутки знакопостоянства
6. Непрерывность
7.
8. Наибольшее и наименьшее значения
9. Ограниченность
10. Выпуклость
СВОЙСТВА ФУНКЦИИ
Алгоритм описания свойств функции
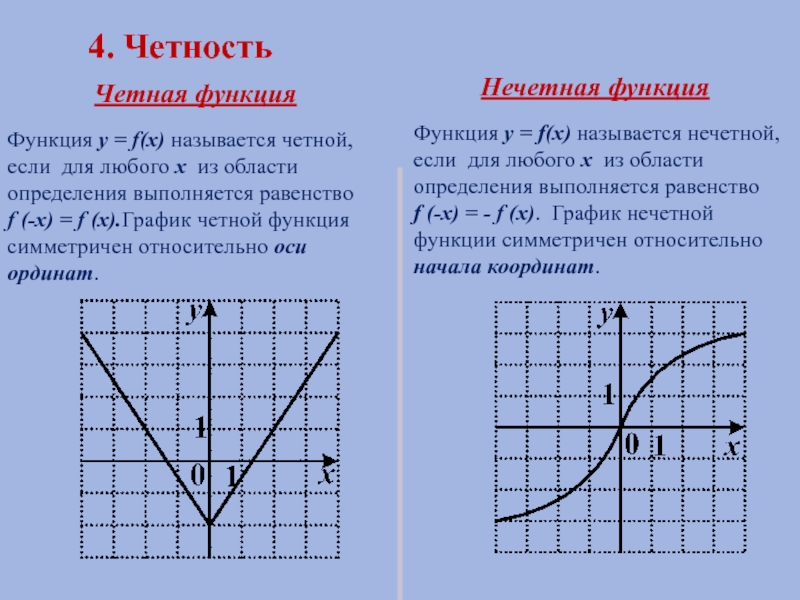
Слайд 74. Четность
Четная функция
Нечетная функция
Функция y = f(x) называется четной, если для
Функция y = f(x) называется нечетной, если для любого х из области определения выполняется равенство
f (-x) = - f (x). График нечетной функции симметричен относительно начала координат.
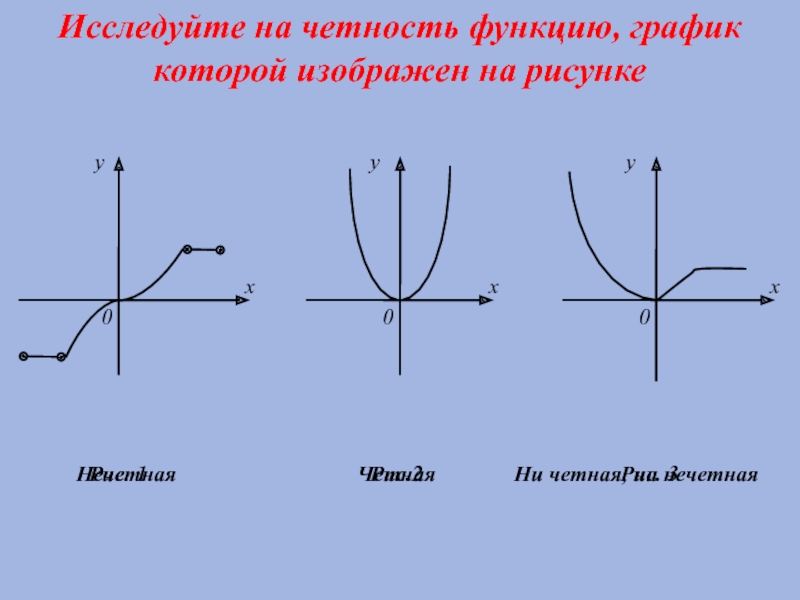
Слайд 8Исследуйте на четность функцию, график которой изображен на рисунке
x
0
y
x
0
y
x
0
y
Рис. 1
Рис.2
Рис. 3
Нечетная
Четная
Ни
Слайд 9АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
y = ax2+bx+c
Определить направление ветвей параболы
Определить координаты
m = -b/2a; n = y(m)
Построить несколько точек, принадлежащих параболе
Соединить отмеченные точки
Слайд 10x
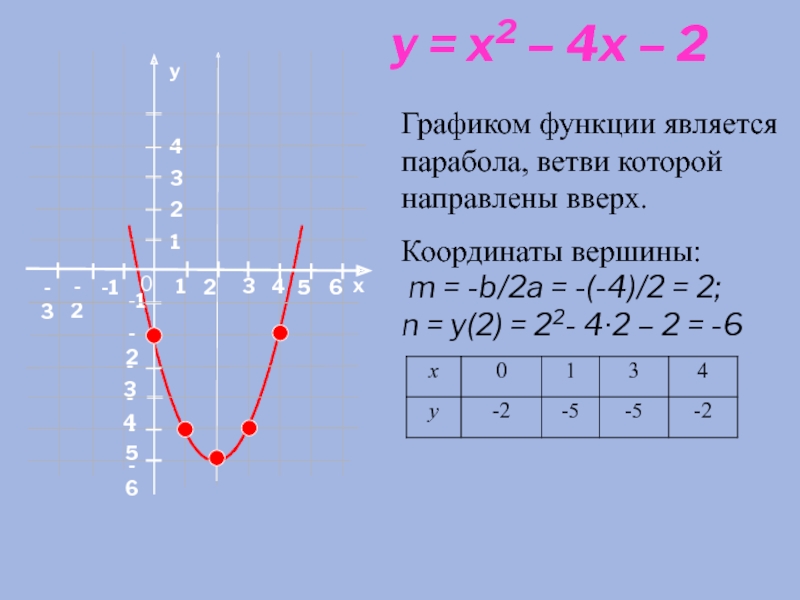
y = x2 – 4x – 2
Графиком функции является парабола,
Координаты вершины:
m = -b/2a = -(-4)/2 = 2;
n = y(2) = 22- 4∙2 – 2 = -6